寻优方法在医学图像配准中性能比较研究
潘梅森, 江建军, 周慧灿, 聂方彦
寻优方法在医学图像配准中性能比较研究
潘梅森1, 江建军2, 周慧灿1, 聂方彦1
(1. 湖南文理学院 计算机科学与技术学院, 湖南 常德, 415000; 2. 湖南文理学院 图书馆, 湖南 常德, 415000)
医学图像配准是以相似性测度为目标函数, 通过多参数优化方法寻找最佳变换参数的过程. 本文以MI为相似性测度, 通过分别使用Powell算法和PSO法等方法寻优得到最佳变换参数, 并对它们的性能进行了比较. 实验结果表明, Powell法适合于单、多模态配准; 虽然PSO法能成功配准, 但是寻优效率有待提高, 有必要在精度和时间效率之间进行适当折中.
医学图像配准; 互信息; 寻优方法; 变换参数
医学图像配准是指对不同时间、不同场景、不同模态的多幅图像进行空间几何变换, 使得代表相同结构的像素(体素)能够达到空间上的一致[1-7]. 在过去的几十年里, 医学图像配准技术取得了快速的发展, 学者们提出了很多实用有效的方法, 其中基于互信息量(Mutual Information,M)技术是目前在医学图像配准中广泛使用的有效方法[8-11]. 它采用互信息量作为相似性测度, 是一种自动的、不需要对图像作任何预处理而直接进行配准的方法. Paul 等人[12]通过使两幅医学图像互信息量最大技术来获取配准的平移和旋转参数, 由于互信息量函数包含了许多局部极值点, 使得获取的旋转角度并不是全局最优值. Fei[13]、Slomka[14]和Radau[15]等人在采用互信息量作为相似性测度基础上, 通过使用Powell法、单纯形法等多参数寻优方法来获取平移和旋转参数[16-17].
1 医学图像配准
1.1 医学图像配准过程
一般说来, 医学图像配准过程由4部分组成: 特征空间选择、空间几何变换、相似性测度、变换参数优化, 如图1所示, 其中, 变换参数优化是这4个组成部分中非常关键的一环.

图1 医学图像配准过程
假设参考图像和浮动图像分辨率均为´像素,级灰度, 左上角像素点位置为(1, 1), 在点(,)的灰度值分别为(,)和(,),为将浮动图像映射到参考图像物理空间的几何变换. 医学图像配准就是找到这样一个空间几何变换, 使得图像和之间的相似性测度最大化的过程, 即:

其中是图像相似性测度. 如果互信息作为图像相似性测度, 则配准可以表示为:


式中()和()分别为参考图像和浮动图像的熵,(,)是图像和的联合熵, 其定义为:

在二维空间, 医学图像刚体变换实质上包括了平移和旋转变换, 即:

1.2 多参数优化方法
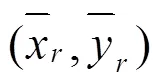

1.2.1 Powell法



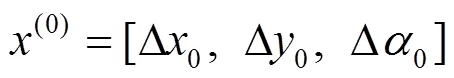
1.2.2 粒子群优化算法
Kennedy和Eberhart提出的粒子群优化(Particle Swarm Optimization, PSO)算法, 是一种新的群智能优化技术[22-24]. 它模仿鸟类的觅食行为, 将问题的搜索空间类比于鸟类的飞行空间, 将每只鸟抽象为一个无质量无体积的粒子, 用以表征问题的一个候选解, 优化所需要寻找的最优解则等同于要寻找的食物. PSO算法通过群体中粒子间的合作与竞争而产生的群体智能指导优化搜索, 算法通用性较强, 具有全局寻优的特点. 但PSO算法也存在局部搜索能力较差、搜索精度不够高、不能保证搜索到全局最优解、容易陷入局部极小解等缺点.




2 倾斜校正方法在互信息医学图像配准中的应用
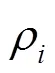


2.1 单模态医学图像配准


图2 CT图像

图3 MR图像
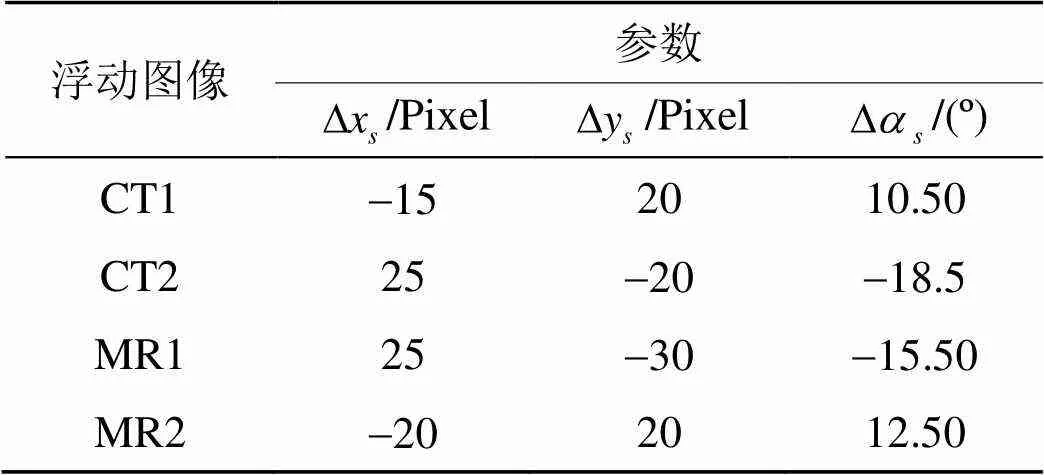
表1 单模态配准时浮动图像实际变换参数



图5 PSO

表2 单模态图像配准性能比较
从表2可以看到, 在单模态配准时, 从配准精度来看, Powell法能成功配准4幅图像, 精度较高, 但是我们发现, 在配准CT1图像时, 得到的平移参数误差稍大; 整体上讲, PSO法配准比Powell法精度高, 在配准CT1、CT2和MR2等3幅图像时, 得到的平移参数和旋转角接近实际变换参数, 误差小, 配准成功, 在MR1配准时, 虽然能成功配准, 但是旋转角误差略大. 至于配准耗费的时间, Powell法在配准4幅图像所耗费时间较短, 尤其是在配准MR2图像时速度最快; PSO法在配准时所耗费时间较长, 相对而言, 在配准CT2和MR1图像时所耗费时间较短, 在配准CT1和MR2图像时所耗费时间较长. 综上所述, Powell法和PSO法均适合单模态配准; PSO法精度较高, 但是效率有待提高, 因此, 如果能在精度和时间效率之间进行适当折中, PSO法应该是一种较好的寻优方法.
2.2 多模态医学图像配准
在本节实验中, 我们选取patient_007头部CT第4层图像和MR_T1_rectified第4层图像作为原始图像, 经过刚体变换后得到实验图像, 分辨率均为256×256像素, 灰度为256级. 实验图像分成2组: 第1组选择CT1作为参考图像, MR1作为浮动图像, 如图6所示; 第2组选择MR2作为参考图像, CT2作为浮动图像, 如图7所示. 每幅浮动图像相对于参考图像的实际变换参数如表3所示.

表3 多模态配准时浮动图像实际变换参数

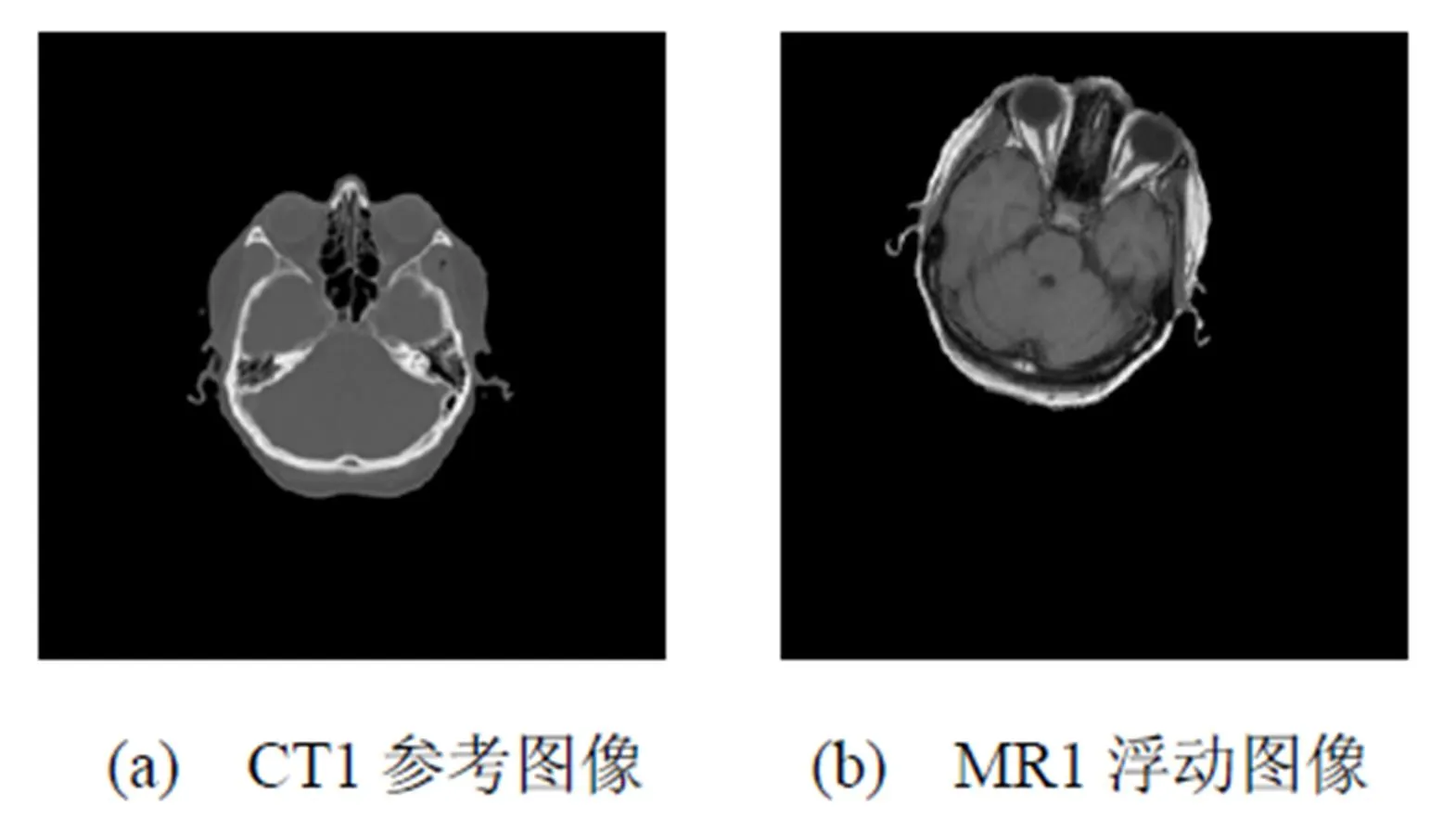
图6 第1组

图7 第2组

图8 第1组配准结果

图9 第2组配准结果
从表4可以看到, 在多模态配准时, 从配准精度来看, Powell法均能成功配准, 得到正确的平移参数和旋转角度, 而且精度较高; PSO法在配准第1组图像时, 得到的方向平移参数和实际变换参数相同, 但是方向平移参数误差偏大, 配准基本成功, PSO在配准第2组图像时, 得到的平移参数误差较小, 但旋转角误差相对较大, 但是仍然能成功配准. 至于配准耗费的时间, Powell法相对较短, PSO法较长, 寻优效率有待提高. 因此, Powell法适合多模态配准, PSO法需要在精度和时间效率之间进行折中.

表4 多模态图像配准性能比较
3 结论

[1] Lu Z T, Feng Y Q, Feng Q J, et al. Medical Image Regis- tration Based on Principal Phase Congruency[J]. ACTA ELECTRONICA SINICA, 2008, 36(10): 1974-1978.
[2] Brown L. A survey of image registration techniques[J]. ACM Computing Survey, 1992, 24(4): 325-376.
[3] Maes F, Collignon A, Vandermeulen D, et al. Multimoda- lity image registration by maximization of mutual inform- ation[J]. IEEE Trans on Medical Imaging, 1997, 16(2): 187-198.
[4] Thevenaz P, Unser M. Optimization of mutual information for multiresolution image registration[J]. IEEE Trans on Image Processing, 2000, 9(12): 2083-2099.
[5] Kybic J, Unser M. Fast parametric elastic image registr- ation[J]. IEEE Trans on Image Processing, 2003, 12 (11): 1427-1442.
[6] Krucker J F, LeCarpentier G L, Fowlkes J B, et al. Rapid elastic image registration for 3-D ultrasound[J]. IEEE Trans on Medical Imaging, 2002, 21(11): 1384-1394.
[7] Rueckert D, Sonoda L, Hayes C, et al. Nonrigid registrati- on using free-form deformations:application to breast MR images[J]. IEEE Trans on Medical Imaging, 1999, 18(8): 712-721.
[8] Maintz J B A, Viergever M A. A survey of medical image registration[J]. Medical Image Analysis, 1998, 2(1): 1-36.
[9] Hyunjin P, Peyton H, Kristy K, et a1. Adaptive registration using local information measures[J]. Medical Image Analysis, 2004, 8(4): 465-473.
[10] Can A, Stewart C. A feature-based, robust, hierarchical algorithm for registration palm of images of the curved human retina[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002, 24(3): 347-363.
[11] Pluim J P W, Maintz J B A, Viergever M A. Mutual- information-based registration of medical Images: A Survey[J]. IEEE Transactions on Medical Imaging, 2003, 22(8): 986-1004.
[12] Paul V, William M, Wells I. Alignment by Maximization of Mutual Information[J]. International Journal of Compu- ter Vision, 1997, 24(2): 137–154.
[13] Fei B, Wheaton A, Lee Z, et al. Automatic MR volume registration and its evaluation for the pelvis and prostate[J]. Physics in Medicine and Biology, 2002, 47(5): 823-838.
[14] Slomka P J, mandel J, Downey D, et al. Evaluation of voxel-based registration of 3-D power doppler ultrasound and 3-D magnetic resonance angiographic images of carotid arteries[J]. Ultrasound in Medicine and Biology, 2001, 27(7): 945-955.
[15] Radau P E, Slomka P J, Julin P, et al. Evaluation of linear registration algorithm for brain SPECT and the errors due ti hypoperfusion lesions[J]. Medical Physics, 2001, 28(8): 1660-1668.
[16] Andersson J L, Sundin A, Valind S. A method for coregi- stration of PET and MR brain image[J]. Journal of Nuclear Medicine, 1995, 36(7): 1307-1315.
[17] Borgefors G. Hierarchical chamfer matching: a parametric edge matching algorithm[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1988,10(6): 849-865.
[18] Pan M S, Tang J T, Yang X L. An algorithm for medical image tilt correction using B-spline and moment invariants[J]. ICIC Express Letters, 2010, 4(1): 57-63.
[19] Pan M S, Tang J T, Yang X L. Tilt Correction Methods for CT and MR Medical Images[J]. Biomedical Engineering Applications, Basis and Communications, 2010, 22(6): 519-533.
[20] Powell M J D. An efficient method for finding the minim- um of a function of several variables without calculating derivatives[J]. Computer Journal, 1964, 7(2): 155-162.
[21] Zhang J, Zhou C W, Zhuo J S. Powell dynamic identifica- tion of displacement parameters of indeterminate thin wa- lled curve box based on FCSE theory[J]. Acta Mechanica Sinica, 2011, 27(3): 452-460.
[22] Kennedy J, Eberhart R C, Shi Y. Swarm intelligence[M]. San Francisco: Morgan Kaufman Publishers, 2001: 61-98.
[23] Shi Y J, Eberhart R C. A modified particle swarm optim- izer[A]. Proc of the IEEE CEC[C]. Piscataway, NJ: IEEE Press, 1998: 303-308.
[24] Clerc M, Kennedy J.The particle swarm - explosion, stabi- lity, and convergence in a multidimensional complex spac- e[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(1): 58-73.
[25] Trelea I C. The particle swarm optimization algorithm: co- nvergence analysis and parameter selection [J]. Informati- on Processing Letters, 2003, 85(6): 317-325.
A performance comparison study of optimization methods for registration of medical images
PAN Mei-sen1, JIANG Jian-jun2, ZHOU Hui-can1, NIE Fang-yan1
(1. College of Computer Science and Technology, Hunan University of Arts and Science, Changde 415000, China; 2. Library of Hunan University of Arts and Science, Changde 415000, China)
Medical image registration, in essence, is the process that the similarity metric is referred to as the objective function, and the multi-parameter optimization method as the tool for obtaining the optimal transform parameters. In this paper, by use of the mutual information as the similarity metric, two optimization methods including the Powell method and the particle swarm optimization method (PSO) are exerted to explore the optimal transform parameters respectively, and their optimizing performances are evaluated and compared. The experimental results reveal that the Powell and PSO methods can cater to both the mono-modality and the multi-modality medical image registrations. Unfortunately, however, the running time of PSO is relatively longer and needs to be substantially reduced. So in order to improve the optimization efficiency, it is very necessary for PSO to counterbalance the registration accuracy and the running time.
medical image registration; mutual information; optimization method; transform parameters
10.3969/j.issn.1672-6146.2011.03.013
TP 391
1672-6146(2011)03-0044-06
2011-09-09
湖南省教育厅优秀青年基金项目(No. 09B071).
潘梅森(1972-), 男, 教授, 博士, 研究方向为医学图像处理技术. E-Mail: pmsjjj@126.com
(责任编校: 刘刚毅)

