基于两道工序加工顺序安排的解法创新
段 渊
基于两道工序加工顺序安排的解法创新
段 渊
(广东科技学院 基础部, 广东 东莞, 523083)
针对一项工程或者一种产品生产的各工序之间复杂的衔接关系, 在加工顺序安排的常规解决办法基础上, 认真分析研究其数字规律, 揭示其数字下的奥秘, 在工序条形图解决办法的基础上进行解法创新, 建立了“数字分析法解法”. 并通过实例分析说明, 能较好地解决原解法的不足, 其实用性、快捷性更强, 工作效率更高.
物流数学;两道工序; 加工顺序; 解法创新
在运筹学或物流数学中对生产作业计划安排问题国内外都有了较成熟的解法思想, 针对两道工序的加工顺序安排问题, 其常规解法是在确定加工顺序后, 利用画工序条形图的方法来具体计算加工所需最少时间数.
1 两道工序加工顺序安排的常规解法
1.1 加工顺序方案的确定
按以下口诀操作:
排好时间表, 从中数最小 (两行一样大, 任意选一行);
属于第1行, 应该尽先排;
属于第2行, 次序往尾排;
划掉已排者, 剩下照样办[1].
即在表中找最小数时, 若属于第1行, 则按从左到右依次放置, 若最小数在第2行(乙设备)应从后向前顺序安排, 因为两台机床的加工顺序相同, 最后得出加工次序. 作加工工序表时, 设备乙上的顺序和设备甲相同, 且任何零件只有在设备甲完工后才能在设备乙上加工, 所以工序图中设备乙条形图可能会不连贯. 即设备乙在中途要被迫停工, 等待[2-3].
例1 某车间生产5种产品, 都要经过甲乙两台设备的加工, 假定每种产品都必须在设备甲上加工完毕后, 才能进入设备乙上加工, 每种产品在每台设备上所需的加工时间如表1所示, 问如何安排这些产品的加工顺序, 可使总的加工时间最短?

表1 加工时间表
解 表1中的最小数2在第1行第2列, 因此先加工产品2, 划去第2列, 剩下的表中数最小者为3, 可以选第1行第4列的3, 第2个加工产品4, 再划去第4列, 剩下的表中数最小的是3, 它在第2行第1列, 所以产品1最后加工, 划去第1列, 剩下的最小数是4, 选第1行第5列的这个4, 所以产品5第3个加工, 划去第5列剩下第3列, 产品3第4个加工, 加工顺序为2, 4, 5, 3, 1是使总加工时间最短的安排, 如表2所示.

表2 加工工序表
1.2 加工所需最少时间的计算
解决方式: 画工序条形图
具体分两种类型:
a. 中途不需要等待的问题;
b. 中途需要等待的问题.
例1 属于中途不需要等待的问题, 解答结果如图1所示.
从工序条形图可见总加工时间为28 d, 设备乙等待2 d.

图1 工序条形图
下面再分析一个中途需要等待的例子.
例2 东莞鸿发家具厂生产4种家具, 都要经过甲乙两台设备的加工, 每种家具都必须在设备甲上加工完毕后, 才能进入设备乙上加工, 每种家具在每台设备上所需的加工时间如表3所示, 问如何安排这些产品的加工顺序, 可使总的加工时间最短?

表3 加工时间表
解 a. 工序安排方案的确定.
表4中最小数3在第1行第2列, 因此先加工产品A2, 划去第2列; 剩下的表中最小数4, 位于第1行第3列, 因此第2个加工产品A3, 划去第3列; 剩下的表中最小数5, 位于第2行第4列, 因此产品A4最后加工. 加工顺序为A2, A3, A1, A4是使加工时间最短的安排[4]. 同理可得方案2工序为A3, A1, A4, A2.

表4 加工工序表
b. 加工所需最少时间的计算.
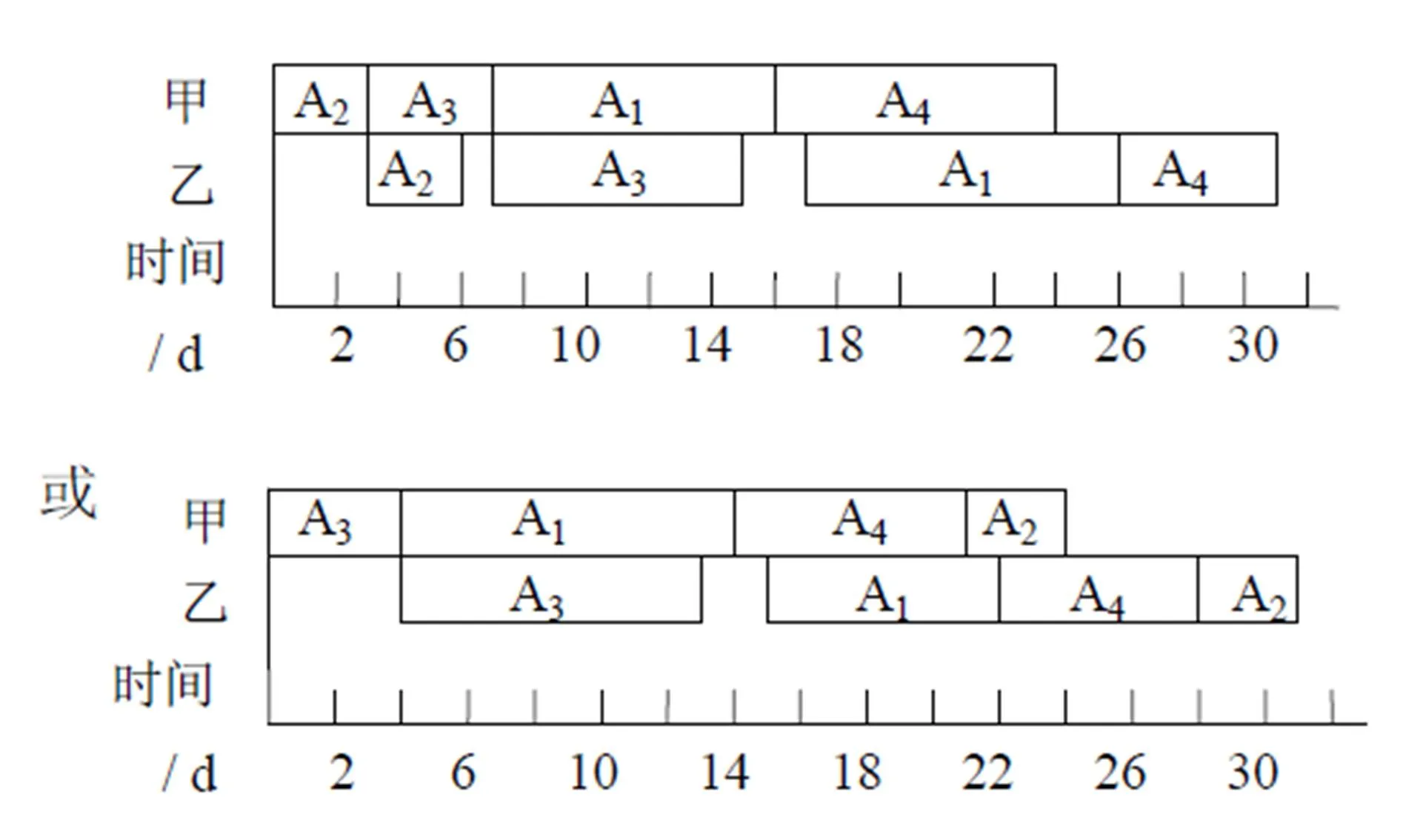
图2 工序条形图
综上, 总加工时间为31 d, 设备乙等待6 d.
上述解法中必须依赖于画工序条形图的方法来确定所需最少时间数, 而画工序条形图方法有它的不足. 当工序较多, 或者两道工序加工但产品类型多的情况下, 仍依赖于画工序条形图的解法有诸多不便, 为了解决画工序条形图方法之不足, 经过认真分析其数字特点与规律, 通过研究对其解法进行创新, 提出创新解法“数字分析法解法”, 该方法还将有利于进行计算机软件运算方法的开发.
2 两道工序加工顺序安排的创新解法
2.1 数字特征分析
关键突破(数字下的奥秘): 中途需要等待的情况是某一产品在设备甲加工未下线, 而此时设备乙已加工完上一产品, 则设备乙不得不停工等待.
例1的数字分析(表2): 易见,
从对例1的数字分析可见, a.-d. 4个算子都取小于符号, 而结果反映设备乙在加工过程中是连续进行的, 中途无需停工等待. 故加工总时间等于所有产品在设备乙上加工的总时间与第1个在甲设备上加工产品的加工时间(即乙最开始时段必须等待的时间, 例1中即为产品2在甲设备上的加工时间)之和.
例2的数字分析(表4).
a. 3 + 4 > 3 + 3, 需要等待, 等待时间为7-6 = 1.
b. 3 + 4 + 10 > 3 + 3 + 8 + 1, 需要等待, 等待时间为17-15 = 2.
c. 3 + 4 + 10 + 7 ≤ 3 + 3 + 8 + 9 + 3, 不需要等待.
总加工时间为3 + 25 + 3 = 31 d, 设备乙等待6 d.
对例2的数字分析: a. 表明当产品A2在第6 h不等式a.右边的数字之和)已从设备乙加工下线, 接下来设备乙按要求要对产品A3进行加工, 但此时产品A3仍在设备甲上加工尚未下线, 要等到第7 h(不等式a.左边的数字之和)后才能从设备甲上生产下线, 因此设备乙不得不中途停工等待, 等待时间为7-6=1;
b. 表明当产品A3第15 h后(不等式b.右边的数字之和)从乙设备下生产下线时, 按工序安排马上进行加工的产品是A1, 但此时产品A1在设备甲上加工仍未下线, 要等到第17 h后才从设备乙上加工下线, 因此设备乙又要再次中途停工等待17-15=2 h.
c. 表明在累计第26 h(不等式c.右边的数字之和)后产品A1设备乙上加工下线, 按工序安排接下来设备乙要进行产品A4的加工, 而产品A4已在累计第24 h就从设备甲上生产下线, 故此时设备乙不需要中途停工等待, 而在加工完上一个产品A1后直接连续加工产品A4. 以上共计中途等待时间为3 h, 设备乙加工总时间为25 h. 从而累计工作时间为: 3 + 25 + 3 = 31 d, 设备乙等待3 + 3 = 6 d.
2.2 数字分析法解法

表5 加工工序表
总加工时间的数字分析法解法:
2.3 应用举例

表6 加工时间表
解 (1)利用口诀确定加工工序如表7所示.

表7 加工工序表
用数字分析算法求加工所需最少时间:
3 结论

[1] 傅维潼.物流数学[M]. 北京: 高等教育出版社, 2005: 77-80.
[2] 张宝雷.物流数学[M]. 北京: 光明日报出版社, 2007: 38-44.
[3] 张莹. 动态规划应用-排序问题[EB/OL]. http://wenku. baidu. com/ view/ e214447d27284b73f2425038. html, 2010-05.
[4] 李军辉.物流数学[M]. 北京: 人民日报出版社, 2008: 53-55.
The solution to the innovation based on the arrangement of processing sequence of two working processes
DUAN Yuan
(Department of Foundation, Guangdong University of Science & Technology Guangdong, Dongguan 523083, China)
The production of a project or a product is made from various working processes and there are far more complicated link-up relations among them. Based on the normal solution to the arrangement of processing sequence, this paper seriously analyzes and studies its numeral law and reveals its numeral secret in order to have the solution to the innovation that is based on the solution to the working process of bar diagram and build up “the solution to the digital analysis method”. With the analysis of the living example, this paper can well solve the disadvantage of the original solution. And it has more practical applicability, easy move and high efficiency.
logistics mathematics; two working processes; processing sequence; the solution to the innovation
10.3969/j.issn.1672-6146.2011.03.010
O 223
1672-6146(2011)03-0033-04
2011-07-20
段渊(1965-), 男, 硕士, 副教授, 主要研究方向为智能信息分析与处理. E-mail: hn_syb@126.com
(责任编校:刘晓霞)

