高速动车组定位转臂载荷谱分布特征研究

朱海斌,李 强

(北京交通大学 机电学院,北京100044)

自2008年以来,我国多条高速铁路客运专线相继建成通车,高速铁路运输技术得到了飞速发展,但是当前发展高速列车仍有许多技术问题需要解决,特别是相关设计规范和试验评定标准尚不完善,需要进行大量的基础研究,从而形成符合我国高速铁路发展的标准和规范。因此建立高速列车关键部件的载荷谱[1-3],并研究其载荷分布特征十分必要。

为了确定定位臂的载荷分布特征,以动车组在我国某运行线路上的实测动应力数据为依据,载荷测试总里程约10 000 km,数据采集利用安捷伦E1401B数据采集系统完成,采样频率为500 Hz,完整体现列车在运行线路上的实际工况及其匹配情况。采用“准静态”法,通过有限元计算出定位转臂的准静态传递系数,识别出运行路段上的实际载荷,采用雨流计数法编制出对应的载荷谱,并研究其载荷特征,为后续的设计和可靠性分析提供重要依据。

1 分析计算准静态传递系数

由于该型动车组拖车和动车定位转臂的结构相同,所以涉及到该结构时不再注明动车还是拖车。建立三维实体模型;利用Hyper works对三维模型进行网格划分;在ANSYS中计算定位转臂的准静态传递关系,定位臂大端距离端面100 mm处施加约束,小端施加100 kN的横向载荷,如图1所示。材料属性值E=211 000 MPa,泊松比为0.3。

目前国内外结构部件载荷标定方法仍然采用应变测量法。对于结构部件、电桥组成的应变测量系统来说,系统输入为载荷(弯矩、剪力、扭力),系统的输出为应变。该方法是在外载荷作用下,通过测量结构部件的应变,来得到载荷的大小。

图1 定位臂加载示意图

根据假设:在使用载荷下,结构保持弹性变形,外载荷与应变呈线性关系。只要选择的贴片点尽量避开应力集中部位,该假设就能成立。因此,首先需要确定载荷传递系数。利用ANSYS有限元分析软件[4]对模型加载,然后估算出传递系数。在利用ANSYS计算准静态载荷传递系数时,单元体越小,约束条件反映实际工况程度越高,估算的传递系数越精确。贴片位置的应力为连续变化的区域(避免应力集中),所以在贴片处载荷传递系数不会因为估算位置的偏差造成较大变化。另外为了更精确的得到载荷传递系数,也可以在贴片后对测试的结构部件进行静态标定获得系数,但是操作上较为复杂,特别是对于大型的结构部件。因此,只要单元体大小选择合适,约束条件反映实际工况,估算位置精确,利用ANSYS计算得到的载荷传递系数能够满足工程应用的要求。本文通过计算得到测点传递系数为k=769.2 N/MPa。

2 数据处理,编制载荷谱

一般情况下转向架动应力的有效频率低于50 Hz,而试验采集频率为500 Hz,该频率足以保证采样数据的真实性。整个测试过程中列车在线路上快速运行,各种干扰信号也会由各测试环节进入数据采集系统,对应力信号产生干扰,因此首先必须进行信号预处理,其次要进行应力-时间历程峰谷值挑选[5-7]。载荷-时间历程的统计方法有很多种,目前应用最广泛的是雨流计数法,该计数方法的突出优点是它与材料的疲劳损伤具有内在联系。对定位臂载荷-时间历程进行雨流计数处理,可得到实测的二维应力谱,即应力均值与应力幅值。为了统计描述上的方便,各级应力幅值组和均值组采用其组中值来表示。然后结合前面计算得到的传递系数,得到相应的二维载荷谱。如表1所示。

表1 高速动车组定位臂实测二维载荷谱 kN

3 载荷特征分布研究

根据经验,大部分承载构件所承受的随机应力幅值可以用威布尔分布来拟合,应力均值则通常服从正态分布,将对载荷幅值和均值进行统计推断。

3.1 分布假设

假设所受的随机载荷幅值服从威布尔分布,所受的随机载荷均值服从正态分布,然后进行假设检验。其分布函数为:

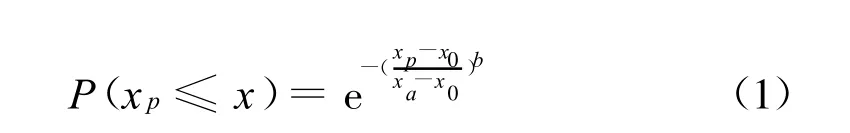
对上式两端取两次自然对数,并令y=-lnln(1/p),x=ln(xp-x0),则得到一元线性关系式:y=a+bx。因此,可以用一元线性回归分析法进行拟合和分布类型的检验。

假设所受的随机载荷均值服从正态分布,正态分布的超值累积频率函数(xp)的表达式为:

3.2 假设检验

根据表1的内容,绘制对应的幅值频率直方图,如图2所示。

图2 载荷幅值频率直方图

从载荷幅值频率直方图的形状来看,近似服从威布尔分布,对载荷幅值和频率进行线性拟合得到:

采用t检验法对拟合曲线进行线性回归效果显著性检验。置信度为95%时,α=0.05,拟合系数的置信区间反映了曲线对数据的拟合精度,区间越窄,说明拟合方案精度越高。

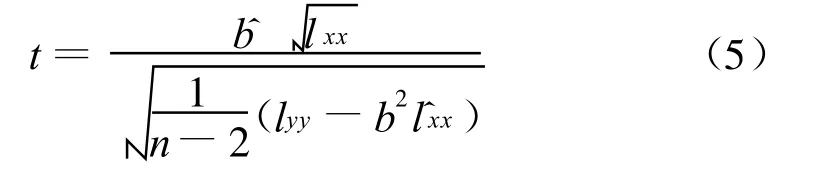
由前面介绍的威布尔分布化简的一元线性模型为:y=a+bx,其中 x=ln(),y=-lnln(1/p),把=3.000,xa=3.642,b=0.592 4 代入,可得 a′=-0.263,b′=-2.303b=-1.364。由表中数据可得:lxx=1.388,=4.56,=15.265,代入式中算得t=64.528,查表得 t0.975(n-2)=2.571,显然|t|≥t0.975(n-2),判定式成立,线性回归方程为 y=-0.263-1.364x。即定位臂载荷幅值密度函数的威布尔分布线性回归效果显著。

下面对载荷均值进行类似分析,根据编制的载谱,绘制载荷均值频率分布直方图如图3所示。

图3 载荷均值频率直方图

从载荷均值频率直方图的形状来看,近似服从正态分布,应用正态分布处理比较合理,利用专用数据处理软件数据拟合功能,对载荷均值和频率进行线性拟合。

同样采用t检验法对拟合曲线进行线性回归效果显著性检验。置信度为95%时,α=0.05。由前面讨论的公式得到正态分布的一元线性模型为:xp=u+upσ,其中xp即为载荷均值,up为标准正态偏量,u和σ为正态分布的常数。

利用最小二乘法[8]来求得常数u和σ得到:

结合表2中的数据,算得 u=3.141,σ=5.201,这样拟合后的直线方程为:xp=3.141+5.201up。根据表的数据可以算得:Luu=31.05,=160.9,Lxx=841.8。代入t检验公式中得到t=27.554,查表得(n-2)=2.571,显然|t|＞(n-2)成立,即定位臂载荷均值密度函数的正态分布线性回归效果显著。

4 结束语

(1)通过以上的分析讨论,本文编制出了高速动车组轴箱定位转臂的二维载荷谱。

(2)从理论上对定位臂载荷特征分布进行了验证,确定了定位臂的载荷均值服从正态分布,载荷幅值服从威布尔分布,为定位臂的设计以及可靠性分析提供了重要的依据。

表2 定位臂载荷均值推断

[1] 张曙光.高速列车转向架载荷谱测试与建立方法的研究[J].中国科学,2008,38(11):1 805-1 814.

[2] P.Heuler,H.Klatschke.Generation and Use of Standardized Load Spectra and Load-time Histories[J].International Journal of Fatigue,2005,(27):974-990.

[3] Glinka,Q and Kam,J.C.P.Rain Flow Counting Algorithm for Very Long Stress History[J].International Journal of Fatigue,1987,(3):2 323-2 380.

[4] 胡国良,任继文.ANSYS 11.0有限元分析入门与提高[M].北京:国防工业出版社,2009:1-3.

[5] 徐其瑞,吕彭明,刘志明.转向架应力谱的统计推断方法研究[J].北京交通大学学报,1998,22(1):44-50.

[6] 徐 宜,刘云鹏,卜树峰.基于雨流法的机械疲劳分析[J].车辆与动力技术,2008,(3):11-14.

[7] 阎楚良,卓宁生,高镇同.雨流法实时计数模型[M].北京航空航天大学学报,1998,24(5):623-624.

[8] 庄楚强,何春雄.应用数理统计基础[M].广州:华南理工大学出版社,2006.