耐热合金蜂窝等效热导率的实验研究①

赵 剑，谢宗蕻，李 玮，田 江

(西北工业大学航天学院，西安 710072)

0 引言

蜂窝夹芯结构是一种先进的轻质结构型式，其通常由上、下2层薄蒙皮和中间的蜂窝芯体组合而成，具有比强度、比刚度高，隔热、隔振性能好等优点，在火箭整流罩、飞机机身、航空发动机短舱、现代卫星等航空航天结构件中得到广泛应用。鉴于上述优点，耐热合金蜂窝夹芯结构也成为高超音速飞行器和新一代可重复使用运载器热防护系统面板的理想方案[1－2]。耐热合金蜂窝夹芯结构用作热防护系统面板，进行设计时必然涉及传热分析。由于蜂窝芯体的几何不连续性，导致其内部传热模式相当复杂，包括金属胞壁的固体导热、蜂窝腔体内的气体导热，以及蜂窝上下面板间的辐射换热等几种不同模式。热分析时，如果对蜂窝芯体和其内部的传热模式进行详细建模将使分析模型过于复杂，通常期望将蜂窝芯体等效为连续的实体，采用蜂窝芯体的宏观等效热导率进行传热分析。

关于蜂窝夹芯结构传热分析方面的研究多采用细观方法，分析蜂窝结构的传热性能[3－7]，而通过实验方法获得蜂窝等效热导率的研究尚比较缺乏[7－8]。文献[9－10]进行了金属蜂窝的传热实验研究，其中文献[9]分析了镍基合金蜂窝板在高温下的防热特性，但并未讨论镍基合金蜂窝的等效热导率;文献[10]对铝蜂窝平板进行了模拟气动加热实验，测定了加热表面和非加热表面的瞬态温度，同样未给出金属蜂窝的等效热导率。

本文针对可在高温环境下工作的Hastelloy X合金蜂窝夹芯结构进行稳态传热实验研究，获取其在不同温度下的等效热导率，并采用Swann-Pittman半经验模型计算其等效热导率。

1 实验

1.1 实验原理

采用稳态方法测量蜂窝夹芯结构试件的宏观热导率。如图1所示，将试件置于加热板上，试件外表面裸露在空气中，通过辐射和对流方式向外界散热。实验中采用氧化锆绝热材料密封试件四周，使绝热材料高度与试件平齐，以阻止热量沿侧向传递。当系统达到热平衡时，可近似视为一维稳态导热情况。

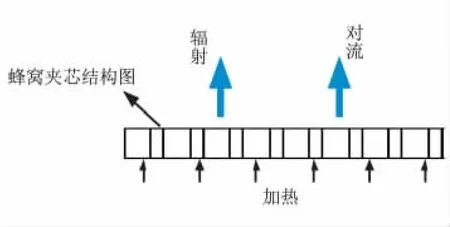
图1 试件传热示意图Fig.1 Sketch of heat transfer modes at the specimen

由傅里叶定律，沿试件厚度方向传递的热流为

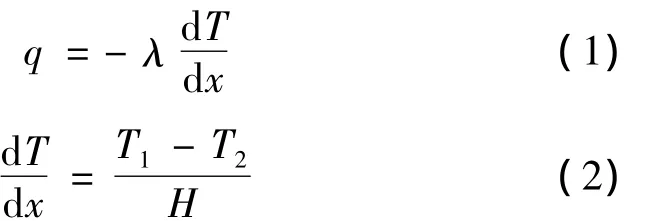
式中q为达到稳态时沿试件厚度方向的热流密度;λ为试件的等效热导率;H为试件厚度;T1、T2为达到稳态后试件上下表面的温度。

系统达到稳态时，试件外表面向环境传递的热量等于从下表面进入试件的热量。

试件上表面以热辐射和热对流形式向环境传递热量。其中，辐射热流由Stefan-Boltzmann定律得

式中 ε为试件外表面的发射率;σ为Stefan-Boltzmann常数，σ =5.67 ×10－8W/(m2·K4);Ta为环境温度。

试件上表面与空气间的对流换热可视作大空间自然对流换热情况[11]。工程上广泛采用如下的实验关联式计算大空间的自然对流换热:

其中:

式中Nu为Nusselt数;Gr为Grashof数，在自然对流现象中，其作用相当于强制对流中的Reynolds数;Pr为Prandtl数;C为常数;α为体积膨胀系数;Δt为壁温与环境之间的温差;ν为流体在定性温度下的运动粘性系数;l为定性长度;g为重力加速度。

恒壁温下，热板上表面平均Nusselt数推荐实验关联式为

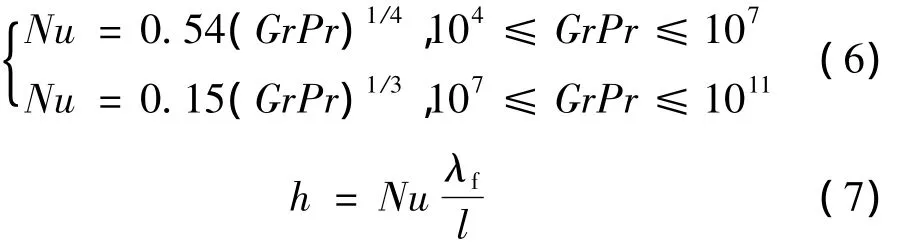
式中l为定性长度;λf为流体在定性温度下的热导率;h为对流传热中的表面传热系数。

对于恒壁温条件下热面朝上的平板自然对流问题，定性长度为平板的表面积与周长之比，定性温度取边界层膜温度:

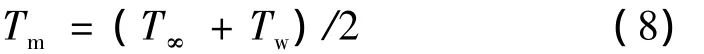
由牛顿冷却公式，对流换热热流为

将式(3)和式(9)叠加，得到试件上表面向外散热的总热流qo，则试件的等效热导率为

由式(10)得到的是耐热合金蜂窝夹芯结构试件的等效热导率，其中耐热合金蜂窝芯体的等效热导率可采用热阻分析方法得到。

蜂窝夹芯结构的总热阻为

蜂窝夹芯结构中的上面板、蜂窝芯体和下面板属于串联导热情况，总热阻等于各串联热阻之和:

式中t1、t2、tc分别为上、下面板、蜂窝芯体的厚度;λf为面板材料的热导率;λc为蜂窝芯体的等效热导率。

联合式(11)、式(12)可求得 λc。

1.2 实验系统与试件

实验系统由大功率高温加热器、可控硅控制器、PSI多通道温度扫描阀、数据采集计算机等组成，如图2所示。测温传感器采用k型快速反应热电偶。

蜂窝夹芯结构试件由耐热合金材料Hastelloy X制成，Hastelloy X合金是一种添加了钴和钨的镍-铬-钼合金，具有较好的高温强度，可在900℃以下长期使用。

试件的几何尺寸如表1所示，Hastelloy X合金材料的热导率如表2所示。如图3所示，在试件的裸露表面靠近中心的部分均匀布置5支热电偶，通过求其平均值来代表试件上的表面温度。本研究制作了表面情况与待测蜂窝夹芯结构外表面相同的标准试件，采用比较法测量其表面发射率为0.54。

图2 实验系统示意图Fig.2 Sketch of the test system

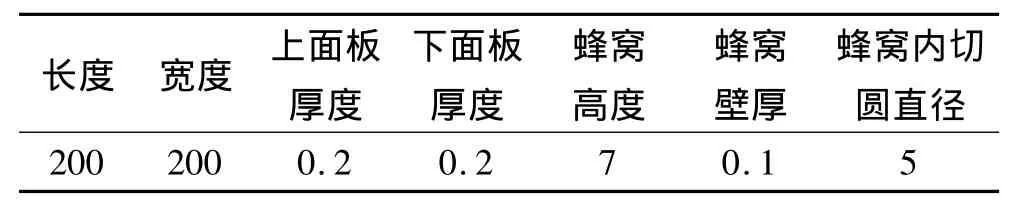
表1 耐热合金蜂窝夹芯结构试件几何尺寸Table 1 Geometries of the refractory alloy honeycomb sandw ich specimen mm

表2 Hastelloy X合金热导率Tab le 2 Thermal conductivities of Hastelloy X alloy

图3 试件实物照片Fig.3 Photo of the specimen

2 理论预测模型

耐热合金蜂窝夹芯结构受热时，蜂窝内部存在的传热模式主要包括金属胞壁材料的固体导热，蜂窝腔体内的气体导热，以及蜂窝腔内面板间的辐射换热等。Swann与Pittman假定蜂窝夹芯结构的面板厚度足够小，采用有限差分法分析蜂窝结构的辐射和导热复合传热问题，提出了蜂窝结构内辐射换热经验公式[7，12]，利用并联模型得到了蜂窝结构等效导热半经验公式:

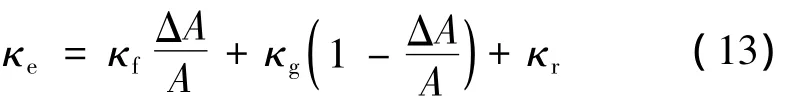
式中 κe为等效热导率，是蜂窝芯几何尺寸和材料热物性参数的函数;κf为蜂窝胞壁材料的热导率;κg为蜂窝腔内气体的热导率;κr为蜂窝芯体辐射换热等效热导率;ΔA/A为蜂窝胞壁横截面积与蜂窝全部面积之比。

气体热导率可由式(14)得到:

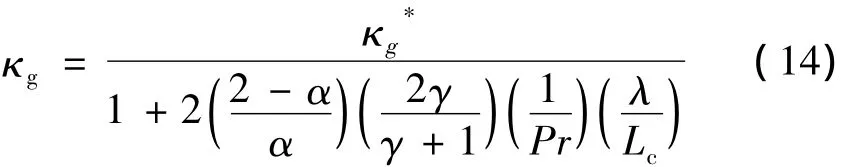
λ值由式(15)决定:

式中KB为波尔兹曼常数;T为温度;dg为气体分子碰撞直径;p为压力。

式中Tavg为蜂窝板的平均温度;σ为斯忒潘-波尔兹曼常数ε为蜂窝内部统一辐射率;d为蜂窝单元尺寸。

利用上述半经验模型预测了文献[13]中的Inconel 617镍基高温合金正方形蜂窝的有效热导率，并与文中提供的实验数据进行对比，结果如图4所示。

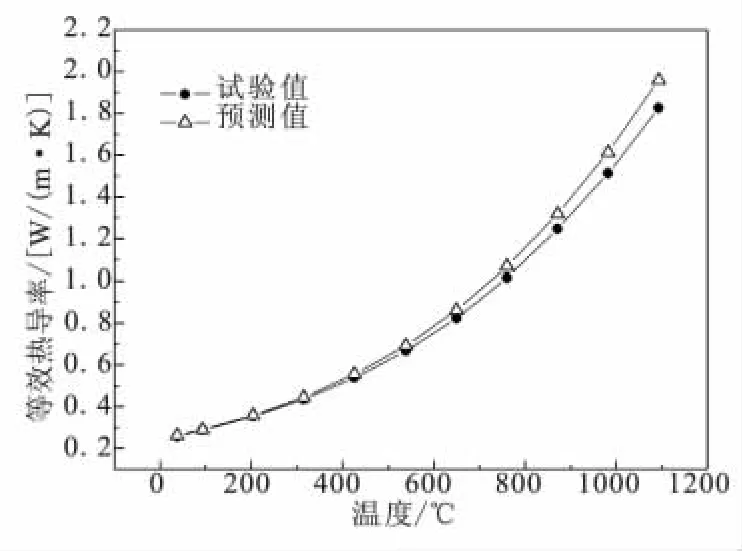
图4 Inconel 617方型蜂窝等效热导率实验值与预测值对比Fig.4 Com parison between tested and p redicted effective thermal conductivities for Inconel 617square honeycomb core

3 结果与分析

图5为一组系统达到热平衡后的蜂窝夹芯板热冷面温度图。平衡后冷面温度较热面温度显著降低，且随着热面温度的升高，热冷面之间的温差逐渐增大，在热面温度达到630℃时，冷面温度为549℃，温差达到81℃。该结果从侧面说明耐热合金蜂窝夹芯结构具有良好的防隔热效果，且随着温度的上升，隔热效果逐渐增强。

利用Swann-Pittman半经验模型预测了本研究中采用的Hastelloy X试件的等效热导率，并与实验测得的热导率进行了对比，如图6所示，两者吻合良好。对比表2和图6还可看出，Hastelloy X合金蜂窝的等效热导率远小于Hastelloy X合金自身的热导率，基本小了一个数量级，验证了蜂窝夹芯结构具有低热导率特征和良好的隔热效果。

图5 平衡状态试件热冷面温度Fig.5 Equilibrium tem peratures of the hot and cool sides

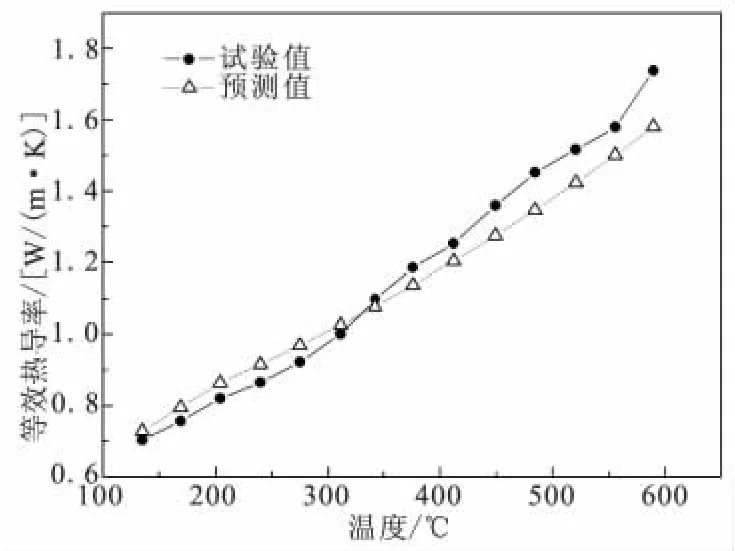
图6 Hastelloy X六边形蜂窝等效热导率实验值与预测值对比Fig.6 Comparison between tested and predicted effective thermal conductivities for Hastelloy X hexagonal honeycomb core

4 结论

(1)开展了耐热合金蜂窝夹芯结构稳态传热实验，得到了一组随温度变化的蜂窝等效热导率;采用Swan-Pitmman半经验模型预测了该蜂窝的等效热导率，与本实验结果对比吻合良好，最大相对误差在10%以内。

(2)温度越高，耐热合金蜂窝夹芯结构的隔热效果越好，耐热合金蜂窝的等效热导率比胞壁材料的热导率小一个数量级。

[1] Max L Blosser.Development of metallic thermal protection systems for the reusable launch vehicle[R].NASA Technical Memorandum 1102996，October 1996.

[2] John T Dorsey，et al.Metallic thermal protection system technology development:concepts，requirements and assessment overview[R].AIAA 2002-0502.

[3] Arulanant ham M，Kaushika N D.Coupled radiative and conductive thermal transfer across transparenthoneycomb insulationmaterials[J].Applied Thermal Engineering，1996，16(3):2092217.

[4] Kamran Daryabeigi.Heat transfer in adhesively bonded honeycomb core panels[R].AIAA 2001-2825.

[5] 唐羽烨，薛明德.蜂窝夹芯板的热学与力学特性分析[J].航空学报，2005，22(2).

[6] Lu T J.Heat transfer efficiency of metal honeycombs[J].International Journal of Heat and Mass Transfer，1999(42).

[7] Swann R T，Pittman CM.Analysis of effective thermal conductivities of honeycomb-core and corrugated-core sandwich panels[R].NASA TND-714，April，1961.

[8] Stroud CW.Experimental verification of an analytical determination of overall thermal conductivity of honeycomb-core panels[R].NASA Technical Note，TN D-2866，June 1965.

[9] 梁伟，张立春，吴大方，等.金属蜂窝夹芯板瞬态热性能的计算与试验分析[J].航空学报，2009，30(4).

[10] 陈勇，高德平.金属蜂窝平板加热过程的数值模拟与试验研究[J].理化检验-物理分册，2003，39(5).

[11] Bejan Dj M M A，Kraus A D.Heat transfer handbook[M].John Wiley＆Sons，Inc，2003.

[12] Carl CPoteet，Hasan Abu-Khajeel，Su-Yuen Hsu.Preliminary thermalmechanical sizing ofmetallic TPS:process development and sensitivity studies[R].AIAA 2002-0205.

[13] Gorton M P，Shideler J L，et al.Static and aerothermal tests of a superalloy honeycomb prepackaged thermal protection system[R].NASA TP 3257，March 1993.