基于平行层推移的含表观裂纹缺陷固体发动机装药燃面计算①
费 阳,胡 凡,张为华,孙明波
(国防科技大学航天与材料工程学院,长沙 410073)
0 引言
装药燃面计算是固体火箭发动机内弹道性能预示的重要内容,其计算精度直接影响发动机性能预示的效果。
目前,已有多种装药燃面计算方法[1],应用较广的有作图法、通用坐标法、实体造型法、解析法、网格推移法。作图法需在图纸上作出初始燃面形状,继续作出燃去肉厚后的燃面图纸,使用测量器具测出燃面面积,该方法不适用于构型复杂的药型,且计算误差较大;通用坐标法通用性较好,但计算某些特殊装药构型时,有燃面跳动,且不能计算含缺陷装药燃面;实体造型法目前被工业部门广泛采用,充分利用CAD软件,与药型设计结合紧密且精度高,但对于结构复杂的药型,推移造型过程十分繁琐,并可能出现奇点,计算无法继续;解析法建立在精确的燃面数学公式上,但只针对形面简单的燃面计算;网格推移法在初始药型上生成三角网格,再利用初始燃面按燃去肉厚生成新燃面,该方法通用性较好,但它处理燃面交汇、分离效果不佳。另外,以上方法无法计算含裂纹装药燃面。事实上,固体火箭在长时间储存过程中,受到各种因素影响,装药可能产生裂纹,若装药存在裂纹,就将整个发动机报废,势必造成大量损失。实践证明,有些含裂纹装药仍能满足发动机任务要求。因此,对含装药裂纹固体发动机进行性能预示是十分必要的,燃面计算是其中的关键与难点。
针对现有燃面计算方法的不足,本文应用Orsher Stanely与 Sethian J A提出的 Level Set界面追踪方法[1-3],并结合孙明波提出的改进 Sub cell fix重新初始化新方法[4]进行燃面计算。其优点是可准确捕捉界面运动过程中形状变化,自然处理界面拓扑结构变化(交错、分离、消失)。但其缺点在于初始燃面定义需通过修改程序定义较为繁琐,结合实体造型软件进行二次开发,可解决这一困难。另外,Level Set方法基于计算网格,计算量较大,计算速度与网格数量有关。对于主频2.0 GHz的计算机,本文算例均耗时5 min左右。可通过并行计算技术,缩短计算时间。
1 基于Level Set方法的燃面计算模型
Level Set方法采取符号距离函数作为高维等值面,其核心思想是将N维曲面利用N+1维方程零等值面来表示。例如,二维平面圆x2+y2=1,可用三维曲面的z=0等值面来代替,z值便是二维平面上任一点到圆x2+y2=1的符号距离。
1.1 控制方程
根据Level Set方法数学思想,作如下定义:
设药柱、包覆层内部为区域Ω1,外部区域为Ω2,区域之间界面即为燃面,记为Γ(t)。记为t时刻为空间点到燃面的符号距离开始计算时,只需将设置区域Ω1内φ值设为某一负值、区域Ω2内φ值设为某一正值即可,经过一次重新初始化,即可将φ值转化为初始距离场,操作简单。
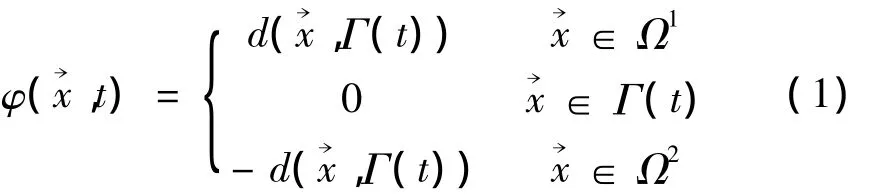
Level Set法捕捉界面的思想是以适当速度推动符号距离变化,得到每一点的符号距离,即可确定界面位置。对燃面法向推移控制方程式(2),空间离散采用五阶WENO格式,时间离散采用三阶TVD-Runge-kutta格式。
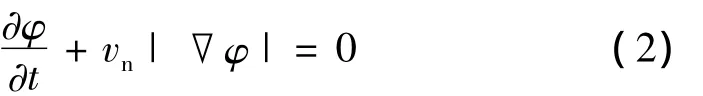
其中,vn为燃面法向推移速度,可为空间、时间、压强及流速等流场参数的函数。求解式(2),可得各点φ值。事实上,只需准确求出界面附近各点φ值便可。利用Narrow Band[1]方法,将求解区域限制在界面附近,可显著减少计算量,时间复杂度为O(N),N为3个坐标方向上平均网格点数。
燃面面积如式(3)计算:
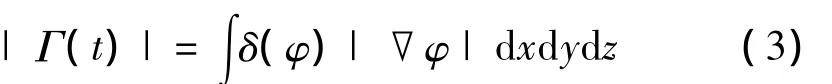
其中,δ为delta函数,标记燃面点。

式中 ε =1.5Min(dx,dy,dz)。
1.2 重新初始化

因此,计算过程中每一时间步都对φ进行重新初始化。采用国防科技大学孙明波提出的改进Sub cell fix重新初始化格式,与传统格式[5-7]相比,效果更佳、收敛速度更快[8]。
2 星形装药算例仿真
算例采用图1所示星形装药,两端包覆,内表面燃烧。主要参数如表1所示。不考虑侵蚀燃烧效应,利用Level set方法对其推移过程进行仿真。

图1 某星形装药构型图Fig.1 Structure of tested star grain
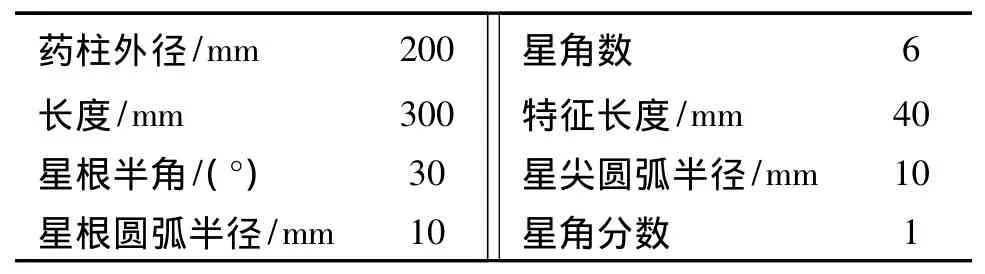
表1 算例装药结构参数Table 1 Structure parameters of tested grain
2.1 算例1——装药无裂纹情况
与实体造型法进行对比,验证Level Set法的准确性。计算网格数量为71×71×101,程序中将包覆层转化为积分限,如果燃面超出包覆层,则不对其积分。图2为装药燃面推移过程,星根部分逐渐消失,星尖不断扩展钝化消失,最终趋于圆面,符合平行层推移规律。可见,Level Set法处理燃面交汇消失的能力较强。
图3为Level set法与实体造型法燃面计算结果对比曲线。二者吻合较好,最大相对误差为4.5%,平均相对误差仅为1.3%。燃去肉厚达50 mm时,部分燃面抵达侧面包覆层,燃面面积迅速下降。

图2 无缺陷装药燃面推移过程Fig.2 Burning surface regression process of a perfect tested grain

图3 燃面曲线对比Fig.3 Com parison of burning surface area lines
2.2 算例2——装药含单条裂纹情况
计算含单个裂纹时装药燃面,考察Level Set方法对复杂构型装药燃面推移的处理能力。
裂纹位于装药正中,宽度3 mm,扇角120°,半径95 mm。计算网格大小为71×71×101。图4为含单裂纹装药燃面扩展过程。
在图4(c)中,可清楚看到裂纹顶部燃面消失,这是燃面“跑出”计算域的结果。实际上,计算域涵盖整个装药,图4(d)中方框内部即为计算域。
图5为装药含1条裂纹与无裂纹情况下燃面肉厚对比曲线。裂纹产生附加燃面,初始时燃面偏大,随着燃烧过程的进行,裂纹顶部燃面最先到达包覆层,使燃面增加速度在5 mm肉厚时放缓;裂纹扩展产生附加燃面,同时裂纹到达包覆层,使燃面减少;二者作用不断抵消,接近10 mm肉厚时,后者作用超过前者,使燃面增速低于无裂纹情况。燃去肉厚30 mm时,大部分裂纹燃面到达包覆,使总燃面低于无裂纹时的情况。

图4 装药含1条裂纹时燃面推移过程Fig.4 Burining surface regression process of a one-cracked tested grain
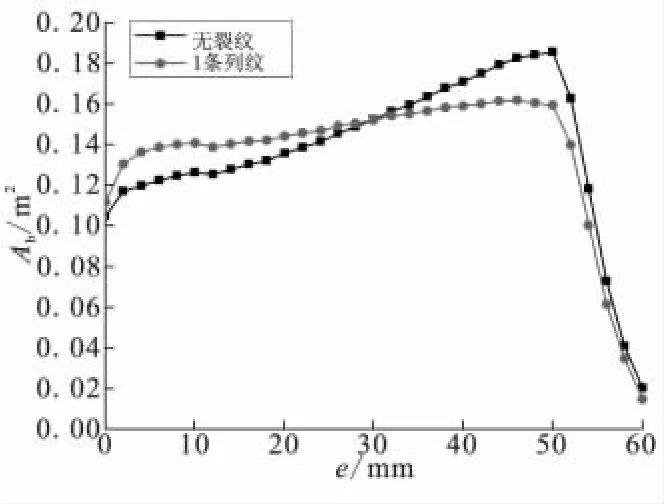
图5 装药含1条裂纹时燃面肉厚曲线Fig.5 Burning surface area of a one-cracked grain
2.3 算例3——装药含2条相邻裂纹情况
利用Level Set方法计算装药含多裂纹时燃面肉厚曲线,考察Level Set方法对多裂纹复杂构型装药燃面推移、交汇过程的处理能力。
裂纹尺寸与上节相同,位于装药中部,两裂纹起始间距34 mm。计算网格大小为71×71×101。图6为含两相邻裂纹装药等速平行推移过程。燃去肉厚接近17 mm时,两裂纹互相交汇,形成1条更大的裂纹继续扩展下去。由此可见,Level Set方法可自然处理多裂纹扩展、交汇等复杂结构变化,效果较好。
图7为装药含1条、2条裂纹与无裂纹情况下的燃面肉厚对比曲线。2条裂纹带来更多的附加燃面,导致起始阶段燃面面积比无裂纹情况时高很多。接近17 mm肉厚时,两裂纹交汇,使附加燃面迅速下降。燃去肉厚25mm时,大部分裂纹燃面到达包覆,总燃面低于无裂纹情况。

图6 装药含2条相邻裂纹时燃面推移过程Fig.6 Burning surface regression process of a two-near-cracked tested grain
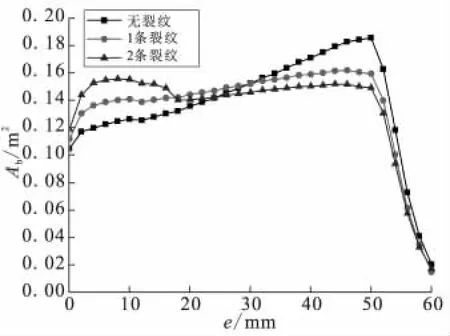
图7 装药含2条相邻裂纹时燃面肉厚曲线Fig.7 Burning surface area of a two-nearcracked grain
3 结论
跟踪Level Set方法最新发展动态,采用全新的改进Sub cell fix重新初始化方法,将Level Set界面追踪方法与固体火箭发动机装药燃面计算相结合,利用Level Set方法,对固体火箭发动机装药燃面推移过程进行了数值模拟,较准确地捕捉燃面变化情况,并计算了装药燃面肉厚曲线,精度较高。采用Level Set方法,对装药含单条、多条裂纹情况进行了燃面计算,准确捕捉裂纹扩展、交汇的过程。可见,Level Set方法对燃面交汇、消失等复杂拓扑结构变化处理能力较强。
实际上,固体发动机药柱常见缺陷(裂纹、脱粘、气泡)都可看作是裂纹。Level Set燃面计算方法是含缺陷装药燃面计算的有力工具。Level Set燃面计算程序易与发动机内流场计算相结合,可实现三维内弹道的模拟。
综上所述,Level Set燃面计算方法有以下3个特点:
(1)可准确计算复杂构型装药燃面,精度高,通用性较好;
(2)自然处理推移过程中燃面交汇、消失等情况,无需特殊处理,应用简便;
(3)可对含裂纹等缺陷装药进行燃面计算,弥补现有燃面计算方法的不足。
[1] 马长礼.固体火箭发动机燃面计算方法研究[D].国防科技大学,2007.
[2] Osher S,Fedkiw R.Level setmethods and dynamic implicit surfaces[D].Spring-Verlag,New York,2003.
[3] 秦飞.固体火箭发动机复杂装药燃面算法研究[D].西北工业大学,2003.
[4] 孙明波.超声速来流稳焰凹腔的流动及火焰稳定机制研究[D].国防科技大学,2008.
[5] Sussman M,Smereka P,Osher S.A level set approach for computing solutions to incompressible two-phase flow[J].J.Comp.Phys.,1994,114:146-159.
[6] Russo G,Smereka P.A remark on computing distance functions[J].Journal of Computational Physics,2000,163:51-67.
[7] Hartmann D,Meinke M,SchroderW.Erratum to“differential equation based constrained reinitialization for level set methods”[J].Journal of Computational Physics,2008,227(22):9682-9696.
[8] Sun Ming-bo,Wang Zheng-guo,Bai Xue-song.Assessment and modification of sub-cell-fixmethod for re-initialization of level set distance function[J].International Journal for Numerical Methods in Fluids,2010,62:211-236.

