基于自助法的土壤导热系数的估计

唐克琴，周树民，管昌生，陈 芸

(1．武汉理工大学理学院，湖北 武汉 430070;2．武汉理工大学土木工程与建筑学院，湖北 武汉 430070)

随着社会经济的发展，环境及能源问题已引起公众的广泛关注，人们对清洁能源的需求逐渐提上日程。在众多能源之中，地热资源凭借其运行费用低、可持续利用及环保等其他能源无法比拟的优点，获得了众多人士的青睐。土壤源热泵系统就是使用地热资源颇具代表性的一种，该系统是利用低品位能源的一种节能环保型技术，通常输入少量的高品位能源，便可把土壤中所储存的低品位能源转化成有用的热能。地源热泵系统设计的关键技术之一是如何根据建筑物的负荷设计埋地换热器，而要准确设计埋地换热器就需要知道建筑物地下土壤的实际导热系数。如果土壤导热系数不准确，则设计的系统可能无法满足负荷要求，也可能导致规模过大，增加成本，因而研究土壤导热系数的估计非常必要。目前国内外对单井孔导热系数的确定已进行了比较深入的研究［1－4］，但在实际工程中，由于土壤的热物性比较复杂，如果利用多打井孔来获得土壤的导热系数，就增加了初期投资。因此，应研究如何以尽可能少的井孔测试数据，尽可能准确地估计整个工程所覆盖的土壤的导热系数。笔者利用自助法将实际获得的几个有限的导热系数用来估计整个工程所覆盖的土壤的导热系数，为埋地换热器的设计提供了一定的参考依据。

1 自助法原理及相关定理

自助法［5］是 EFORN教授于1979年提出来的，是一种主要针对通常的统计方法不能奏效时的估计参数置信区间的方法，比如由于观测值太少而不好估计的情况。简单地说，自助法就是利用计算机来重复模拟试验的方法。利用自助法，一系列新的实地采样数据实验可以不进行，且最初的采样数据又得到充分利用。但自助法和蒙特卡罗模拟法是有区别的，自助法不需要实验重复进行，而是利用原始数据重新生成数据从而实现对总体的估计。从数据处理的角度来看，自助法的原理可以用图1表示。

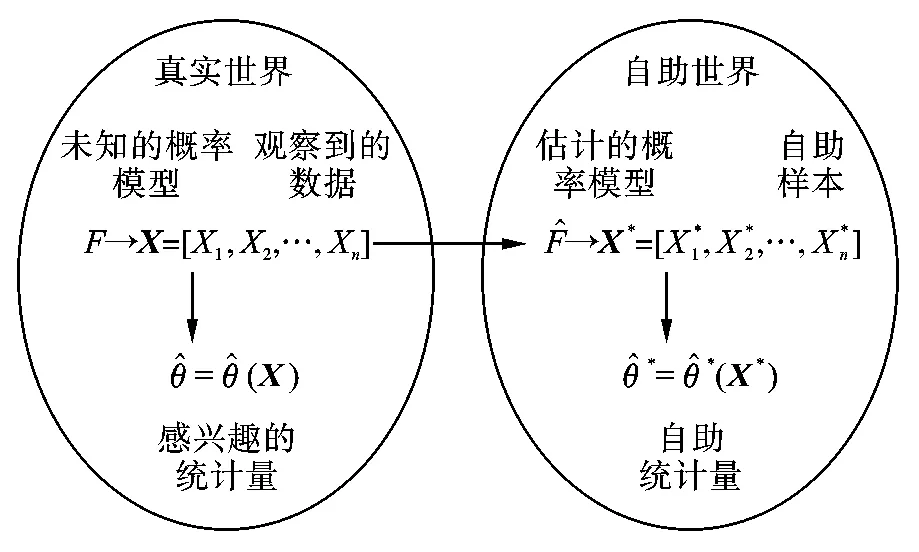
图1 自助法的原理图

定理1［6］给出一组随机样本 X=［X1，X2，…，Xn］，考虑均值统计量 θ=E［X］，则 θ的样本均值为从X中有放回地随机抽取样本 X*=［X*1，X*2，…，X*n］，称之为自助样本，可得相应的自助样本均值为。若E［X2］＜∞，则，这里prob*［·］为自助样本的概率。

2 自助法估计均值和方差的步骤

设随机变量 X=［X1，X2，…，Xn］是总体分布F(x)未知的独立同分布样本，即Xi～F(x)，i=1，2，…，n。用θ表示均值，用σ2表示方差，则估计均值与方差的具体步骤如下:

(1)根据实验获得样本观测值x=(x1，x2，…，xn)，则可得样本的均值和方差为θ。再由观测值构造经验分布函数:

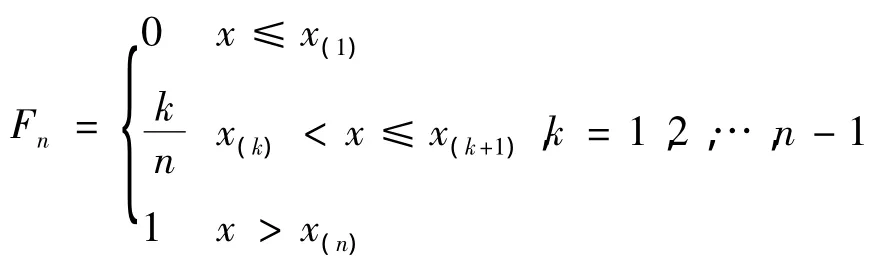
式中:x(1)为子样观测值(x1，x2，…，xn)中最小的一个;x(k)为子样观测值中第k个小的数。

(2)按分布Fn从x中随机有放回地抽取自助样本

3 评价估计量好坏的准则

3．1 偏差估计

所谓无偏估计［8］是指随机变量没有系统性误差的性质，在统计学上称作无偏性，定义如下:设为母体 ξ的概率函数{f(x:θ):θ∈Θ}的未知参数θ的一个估计量，若对一切θ∈Θ，关系式成立，则称为 θ的无偏估计，否则称为有偏的。根据定义可知统计量分别为σ2的无偏估计量和有偏估计量，那么，可以利用公式来估计偏差，在自助法中，可以用来计算，式中B为重复B次抽样，并计算得 B 个

3．2 自助法均值的置信区间

在自助法中，估计均值置信区间的前4个步骤与估计均值的步骤一致，后面还要增加两个步骤:

(2)置信区间的计算，置信度为100(1－α)%的置信区间为，其中 q1=［Bα/2］，q2=B －q1+1。

4 工程实例

4．1 自助法抽样

该工程为湖北省武汉市某高档别墅区的一期工程，建筑面积约为12 000 m2。利用太阳能热水器提供生活用热水，建筑空调采用地埋管地源热泵系统。对现场进行地质勘察和热物性检测，得到4个井孔 1．0～17．6 m的导热系数为:1．057 984 204，1．075 561 695，1．086 150 920，1．106 196 852。

利用 X=［1．057 984 204 1．075 561 695 1．086 150 920 1．106 196 852］抽取 10 000 个容量为4的自助样本:，其分布图如图2所示。

4．2 均值估计

从获得的10 000个自助样本中，计算得自助样本的均值:，其分布图如图 3 所示。

4．3 方差估计

从获得的10 000个自助样本中，计算得自助样本的方差:，其分布如图 4 所示。

4．4 偏差估计

样本均值的置信度为95%的置信区间为［1．102 9，1．1036］，方差的有偏估计误差为－2．551 2 ×10－6，无偏估计误差为－7．815 2 ×10－5。

图2 自助样本的分布图

图3 自助样本均值的分布图

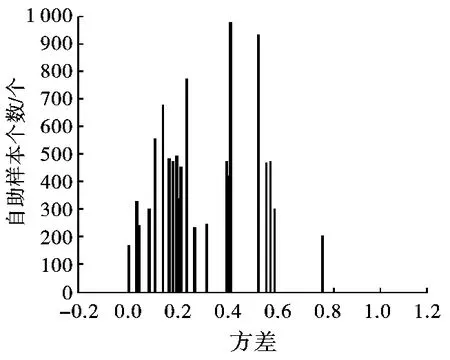
图4 自助样本方差的分布图

5 结论

给出了一种统计推断土壤导热系数的新方法，即利用自助法将实际获得的4个土壤导热系数抽样成40 000个导热系数，并对样本的均值和方差进行了估计，进而对估计做了偏差分析，其结果比较理想，为导热系数的估计提供了新思路。

［1］ 付文彪，蒋绿林，纪洪林，等．地源热泵设计中两个重要参数的实验研究［J］．暖通空调，2009，39(2):116－118．

［2］ 高青，余传辉．地下土壤导热系数简化柱热源模型的确定方法［J］．太阳能学报，2007(12):54－57．

［3］ 高青，余传辉，马纯强，等．地下土壤导热系数确定中影响因素分析［J］．太阳能学报，2008(5):32－36．

［4］ 周亚素．土壤导热系数的现场测试方法［J］．东华大学学报:自然科学版，2008(4):89－92．

［5］ EFRON B．Bootstrap methods:another look at the jackknife［J］．Ann Statist，1979(7):1 － 26．

［6］ ABDELHAK M，ZOUBIR D．Robert iskander bootstrap techniques for signal processing［M］．［S．l．］:［s．n．］，2004:144 －163．

［7］ 戴邵武，高华明，肖支才．基于自助法的小样本数据分析方法研究［J］．海军航空工程学院学报，2009(1):65－68．

［8］ 魏宗舒．概率论与数理统计教程［M］．北京:高等教育出版社，1983:78－96．