一种检验GNSS相位模糊度整周解算有效性的方法

阳仁贵,刘根友,柴艳菊

(中国科学院测量与地球物理研究所动力大地测量学开放研究实验室,湖北武汉430077)

0 引 言

GNSS高精度快速相对定位需要利用高精度的载波相位观测值,载波相位观测值存在着初始的整周数偏差,即初始模糊度,该模糊度是未知的,只有正确地确定了模糊度后,载波相位才能转化为精确的伪距进行精密定位计算。双差相位模糊度具有整数特性,这是提高定位效率和精度的前提条件。

但是相位模糊度整数周计算没有直接解算算法,常用的方法是依据不同的优化准则,在设定的整数空间通过合适的搜索算法实现的。在模糊度的搜索算法中,最简单的算法是在搜索空间内遍历所有的模糊度整数组合,通过比较计算,选取使得模糊度残差带权2范数最小的整数组合为模糊度的固定解,该方法又简称枚举法。显然它的搜索效率是最低的,因为它完全忽略了模糊度之间的一些确定性的先验信息。为了提高模糊度的解算效率,国内外许多学者做了大量的研究工作,提出了一些高效的模糊度整数周固定算法,如基于坐标域的模糊度函数法(AFM);基于模糊度协方差阵的快速模糊度解算法[1](FARA)、最小二乘搜索法[2](LSAST)、Cholesky分解算法、快速模糊度搜索滤波(FASF)、最小二乘降相关法[3](LAMBDA);另外还有用约束方程解模糊度法(ARCE)、附加模糊度参数的卡尔曼滤波法[4]、局部最小值法、模糊度解算新方法[5-6]等。

在模糊的整数集空间内依据搜索准则固定模糊度为整数周时,当观测值中不包含任何随机性和系统性的误差时,搜索固定的模糊度就是正确的模糊度,不需要任何检验过程。但实际上,在进行GNSS观测的过程中,必然会受到各种误差源的影响,从而导致观测量中包含多种误差,这些误差虽然已经经过合适的处理,但其残余误差仍然会导致估计结果为有偏的,从而导致模糊度解的不确定性。对精密的快速定位和导航来说,必须保证模糊度整数解的正确性,所以需要采取一定的措施在最大程度上抑制估计结果的有偏和不确定性。

为了验证模糊度整数解的可靠性,需要对模糊度固定结果进行合适的假设检验。现在采用的假设检验方法,主要基于两种类型的信息:载波相位观测量的残差和来自伪距的测站位置解,在一定程度上能确保模糊度解的可靠性。

模糊度整数解的检验[11-13]是模糊度解算的关键内容之一。只有通过各项检验,才能确认模糊度的整数解是可靠的,才能回代入原方程重新解算基线分量。否则,说明模糊度解算失败,需要增加新的观测数据,重新搜索固定模糊度。

本文在此新的检验方法的基础上,提出了一种模糊度候选值再分析方法,可有效提高模糊度整数解确定的成功率。

1 相位整周模糊度搜索计算

忽略电离层和对流层等系统误差的影响,GNSS相位观测值相对定位双差方程线性化形式可如下表示:

式中:A为基线分量设计阵;B为模糊度参数系数阵;x为基线向量参数;a为双差模糊度参数;W为双差观测值权阵。

如果选用等权观测,那么双差权阵W可以表示为

式中:n表示观测卫星个数;i和j分别表示矩阵的行、列号。

由最小二乘原理,可解得基线分量和模糊度浮点解为

用平差因子阵JA生成等价方程后,可直接解算出模糊度的实数解和误差方差阵为

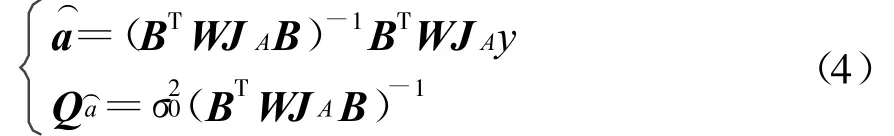
式中,JA=I-A(ATWA)-1ATW.

同理,可得消除模糊度后的基线分量的估计值和协方差阵为

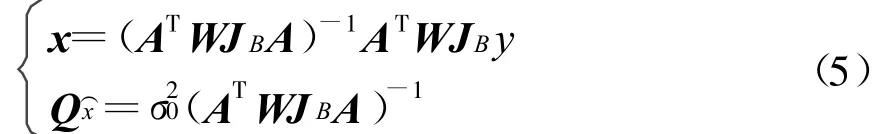
式中,JB=I-B(BTWB)-1BTW

依据正交分解方法,有如下的二次目标函数分解形式[2]:

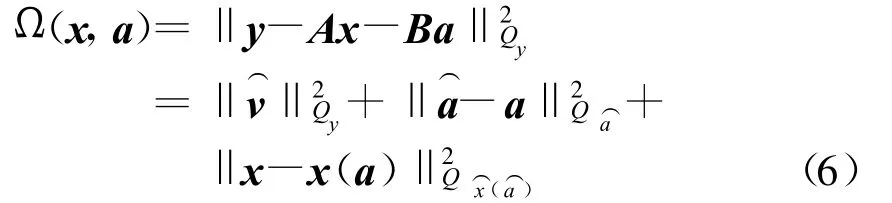
式(6)右边的第一项是最小二乘估计后观测量残差加权平方和,它是常数。第三项中因Qx⌒(â)为正定阵,而x为实数解。由于目标函数的最小值是在第二项为最小时取得的,故模糊度的优化准则为

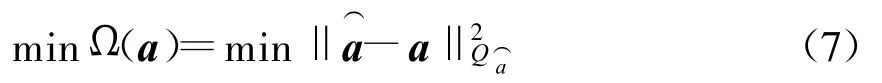
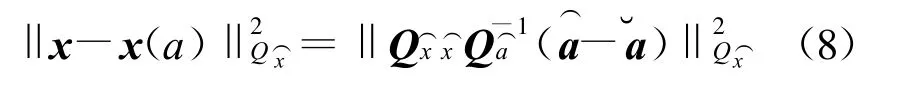
2 Ratio值检验的改进

在模糊度的检验中,用得最多也最简单直观的方法是Ratio显著性检验。

建立Ratio显著性检验如下

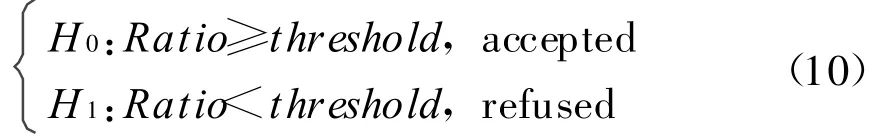
限值threshold根据经验预先给定。一般实践中,设定范围为2～3。有的研究者称上述Ratio为F-ratio,即F假设检验。

另外还有W检验[11],其表达式为

式中:Qd是d的协因子阵;σ2为协方差因子;TW服从学生氏t分布,可以设定合适的置信区间,判断模糊度的可靠性。

以上的Ratio值检验法只是简单地判断模糊度整数解与实数解残差赋权最小2范数。式(6)右边实际包含有三项,而 Ω(a)只是代表了其中的第二项,虽然其优化结果一样,但是进行Ratio检验时,其比值有差异。依据最小二乘优化准则,应该兼顾基线分量部分的范数以及观测值残差范数的大小。

因此,改进原来的Ratio值计算如下:

式(13)表示的Ratio,其threshold值的取值范围可先验地定为 1.5～3。只有当 Ratio大于threshold,才认为模糊度是可靠的,否则,模糊度是不可靠的,还需要运用新的方法提高模糊度的解算成功率。

3 模糊度候选值再分析法

对于快速定位的模糊度解算问题,因存在多路径效应误差和其它的残余误差的影响,当仅仅用模糊度的整数解与实数解的加权平均和来确定模糊度时,其Ratio检验将可能通不过,或者通过检验也不一定是正确,故需要应用新的判别准则进行再分析,以促进模糊度可靠性和成功率的提高。

由优化准则搜索模糊度,在输出的模糊度候选值中,有可能是范数次小、或者范数次次小等对应的模糊度整数解是正确的整数解。这时,Ratio值检验一般都通不过。但我们可以输出多组模糊度解,然后用新的检验准则对输出的多个候选值进行验证,以甄别出正确的模糊度整数解,这就是候选值再分析方法。

对同一组模糊度的整数组合进行兼容性验证。在搜索输出的几组模糊度向量中,把模糊度分为主模糊度组和从模糊度组,主模糊度组中模糊度个数为3个以上。假设主模糊度搜索固定正确,可以用它推导出从模糊度组中的模糊度。这时,推导出的从模糊度组也接近整数值,从而可以通过直接取整得到。因此,我们可以利用该方法检验输出的候选模糊度组内部是否统一,即由其中的多个模糊度(3个以上),计算同组中其它的模糊度,看计算出的模糊度与前面用搜索算法输出的模糊度整数解是否一致,如果一致,说明模糊度组中的模糊度是兼容的,寻找所有兼容的模糊度候选值作为“准模糊度整数解”。

对多个兼容的“准模糊度整数解”,回代入原来的法方程,计算模糊度固定为整数的基线分量解和然后对的大小进行排序,以式(13)表示的方式,如果比值大于上述给定的下限值(threshold),可初步判定最小范数对应的整数组合为正确的固定解。另外,“准模糊度整数解”回代入原方程,并重新进行最小二乘估计,可以得到新的基线分量解,再计算模糊度固定后的基线解与固定前的实数解之间的差值的加权平均和(权为基线分量协方差阵的逆阵),即计算基线向量的偏噪率。

基线的偏噪率(BNR)的计算公式如下:

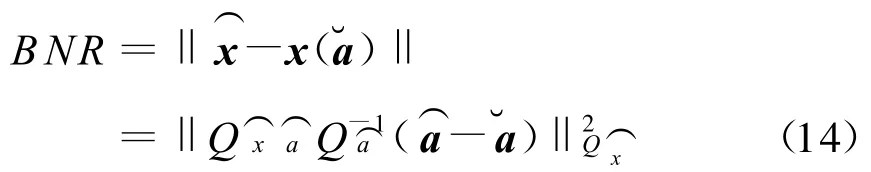
当“准模糊度整数解”通不过Ratio值检验时,可以根据计算的BNR进行排序,选最小的偏噪率对应的模糊度整数解为最终的模糊度整数解,这样能显著提高模糊度的成功率。后面用数值算例验证了这些思路。

4 算例分析

4.1 模糊度整数解检验

实验基线数据为200个历元的静态单频数据(L1),数据采样间隔为1 s,基线长度约为3 km。两测站的共视卫星为6颗,它们组成的5个卫星对分别为27-11,27-8,27-31,27-28,27-7。数据预处理结果显示,相位没有发现周跳现象,模糊度的正确值为a=[-10 -8 11 -37 -25]T。

分别利用不同的历元的观测值进行最小二乘模糊度实数解估计,然后应用搜索算法进行整周模糊度搜索,输出最终确定的5个模糊数残差范数最小的整数组合,同时也输出相应的范数和基线向量偏噪率,并用改进前和改进后的两种Ratio检验方法进行可靠性检验。

下面只列举用历元号为22、24、30、40、120计算结果,浮点解用选权拟合解法估计[8]。表1为不同历元进行模糊度解算的结果。

其中模糊度范数根据式(6)右边第二项计算。两种Ratio检验方法的计算方式为

基线分量的偏噪率(BNR)的计算公式为

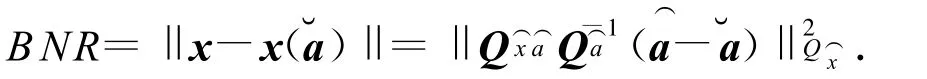
表1显示,历元22、24、30、120的计算结果中,模糊度Ratio1的值均大于2.0,但是仅仅历元120最小模糊度范数对应的模糊度整数组合为正确的整数解,其它的均不是最小范数,历元22的正确模糊度范数排在倒数第四位,历元24的正确模糊度范数排在倒数第三位,而改进的模糊度Ratio2,仅历元120大于1.5,所以该历元的模糊度整数解是可靠的,其它历元模糊度是不可靠的,这证明了Ratio1检验方法的不可靠,而改进的第二个Ratio检验反映了模糊度整数解可靠性。

在模糊度解算不可靠时,即Ratio2小于1.5时,要么是增加观测数据重新解算模糊度整数,要么是应用新的模糊度确定准则来判定模糊度正确值。本文研究了依据基线分量的偏噪率(B NR)来确定模糊度的整数解。表1表示,正确的整数解对应的基线分量的偏噪率均为最小值,因此依据该准则,可以很容易地从候选多组模糊度整数解中选出已经存在的正确的整数组合。表1是每个历元模糊度候选值都输出范数最小的5组,如历元22,依据偏噪率BNR值,可以选定第4组为最终整数解,而历元24是选择第2组为最终整数解。结果显示,依据该准则,显著地提高了正确模糊度整数解解算成功率。

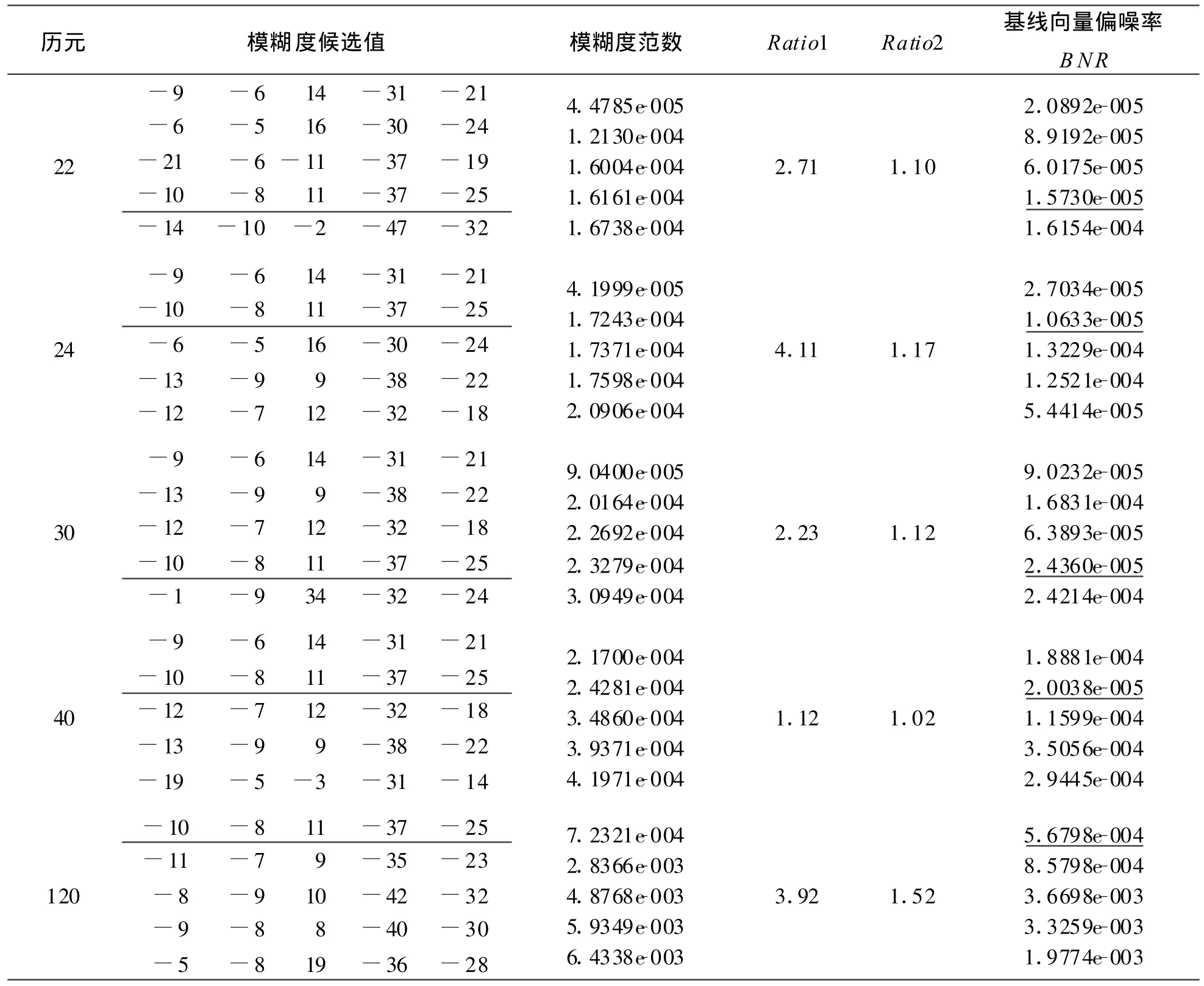
表1 不同历元号的模糊度解算结果

4.2 模糊度整数候选值再分析法确定整数解

从以上算例的结果分析可知,如果模糊度检验通不过,也并不意味着模糊度解算完全失败,我们还可以通过“模糊度候选值再分析法”,在候选值中寻找正确的模糊度整数解。由上述算例可知,模糊度正确值在候选模糊度组中的顺序与最小的BNR值所在的位置对应,故采用“候选值再分析法”能提高模糊度计算的成功率。依据该思路优化快速定位实时解算的算法,可以实现快速定位高效实时解算的功能。

本实验利用了多条GPS基线实测数据进行计算和分析。由于篇幅有限,这里只简单介绍对2003年2月18日观测的一条长约3 km基线的GPS静态观测数据进行单历元解算一些情况。该数据的采样间隔为2 s,共有2443个可用的观测历元。计算时以PRN31卫星作为参考卫星。

应用全部观测历元数据用计算的L1和L2相位双差整周模糊度为[-2 -5 -4 -3 -5 3 1 2 2 2]T。固定的模糊度整数解代入原方程,求得基线分量参数的估计值为[-0.1543 0.5527 0.6189]T,与伯尔尼软件利用全部数据计算的实数解[-0.1569 0.5505 0.6155]基本一致,说明计算结果是可靠的。

对全部2443个历元进行单历元解算,采用P码与相位组合的方法避免秩亏问题。计算结果显示,单历元模糊度候选值再分析法确定的整数解的成功率达到100%。

图1为1000个单历元解与正确整数解的差值的变动范围和趋势。水平方向为历元号,纵方向为基线分量解的差值,单位m。结果显示,单历元解的精度在2 cm以内。

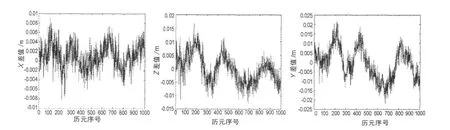
图1 单历元定位获得的基线分量与全部历元计算结果差值

5 结 论

相位模糊度整数周解算的第二步和第三步是固定模糊度值为整数和整数解的检验,这也是模糊度分离算法的关键内容。好的搜索算法有助于实现模糊度高效搜索,好的检验方法可以保证模糊度整数解的可靠性和成功率。本文主要针对模糊度最终整数解的确定,分析了已有模糊度Ratio检验方法的不足,提出了一种更可靠的Ratio检验方法。实验结果显示,该检验方法能可靠地判定最小模糊度范数对应的模糊度整数组是否为可靠的模糊度整数解。

同时,考虑到模糊度检验通不过的情况,为避免直接判定模糊度解算失败,设计了一种“模糊度候选值再分析法”,在模糊度范数较少的几组候选值中寻找正确的模糊度整数解,以达到提高模糊度解算成功率的目的。实验结果显示,应用该方法能显著地提高模糊度整数解确定的成功率,从而促进了实时高精度定位的实现。

[1] Frei E,Beutler G.Rapid static positioning based on the fast ambiguity resolution approach“FARA”,theory and first results[J].M anuscripta Geodaetica,1990(15):325-356.

[2] Teunissen P J G,Odijk D.Rank-defect integer estimation and phase-only modernized GPS ambiguity Resolution[J].Journal of Geodesy,2003,76(9-10):523-535.

[3] 陈小明.高精度GPS动态定位理论与实践[D].武汉:武汉测绘科技大学,1997.

[4] Hatch R,Sharpe T.A computationally efficient ambiguity resolution technique[J].ION GPS-2001,2001:1558-1564.

[5] Ou J K,WANG Z J.An improved regularization method to resolve integer ambiguity in rapid positioning using single frequency GPS receivers[J].Chinese Science Bulletin,2004,49(2):196-200.

[6] Zhu J,Ding X,Chen Y.Maximum likelihood ambiguity resolution based on bayesian principle[J].Journal of Geodesy,2001,75(4):175-187.

[7] Han S,Rizos C.Improving the computational efficiency of the ambiguity function algorithm[J].Journal of Geodesy,1996(70):330-341.

[8] 阳仁贵,欧吉坤.提高GPS单频相位模糊度解算成功率的新方法[J].南京航空航天大学学报,2005,37(3):280-283.

[9] 杜春花,袁 信,范胜林.基于白噪声滤波技术及零空间约束的单频 GPS模糊度解算方法[J].GPS World of China,2002,27(2):1-6.

[10] 刘根友,朱耀仲,韩保民.GPS单历元定位的阻尼LAMBDA算法[J].武汉大学学报.信息科学版,2004,29(3):195-197.

[11] 陈永奇.一种检验GPS整周模糊度解算有效性的方法[J].武汉测绘科技大学学报,1997,22(4):342-345.

[12] Wang J,Satirapod C,Rizos C,et al.Stochastic assessment of GPS carrier phase measurements for precise static relative positioning[J].Journal of Geodesy,2002,76(2):95-104.

[13] Tiberius C C J M,Kenselaar F.Estimation of the stochastic model for GPS code and phase observables[J].Survey Review,2000,35(277):441-454.