GPS水汽反演技术在四川地区的应用研究

陈 澍,熊永良,张绪丰,黄丁发

(西南交通大学空间信息工程中心,四川成都610031)

0 引 言

近年来,随着GPS技术的迅猛发展,地基GPS水汽反演作为一门新兴技术取得了长足进步。GPS遥测大气的设想最早由美国学者Askne于1987年提出[1]。在随后的几年里Bevis等人进行了多次试验,证明了地基GPS水汽反演技术的可行性[2-4]。之后,其他发达国家如日本、德国、瑞典等也开始重视GPS水汽反演技术,取得了一系列研究成果并开始应用于大气研究和气象预报业务中[5-7]。我国从20世纪90年代起开展了地基GPS气象学的研究工作,在上海、北京、香港、广州、武汉[8-12]都取得了较好的成果。在四川地区,李国平、吕弋培、殷海涛等人也做了相关的试验[13-14]。

许多国家建立了GPS连续运行网络来监测大气水汽变化情况,例如美国的 CORS、德国的COGPS、日本的GEONET、中国上海的SCGAN。四川地区也建立了自己的GPS网络,但此网络缺少气象观测仪器,不能提供站点的气压、温度信息,同时天顶静力学延迟模型和加权平均温度与水汽反演精度关系密切,基于上述存在的问题,进行了试验分析。确定了适合四川地区的计算ZHD模型,建立了四川地区Tm计算公式,并说明了此公式的质量,使用GPT模型(全球气压和温度模型)代替实测气象数据进行试验分析,讨论了利用GPT模型反演水汽以及预报降水的可行性。

1 计算Z HD模型的选择

常用的三种模型[15]计算Z HD如下表示:

Hopfield模型:

Black模型:

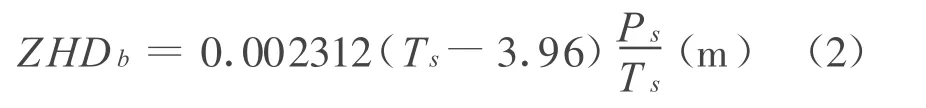
Saastamoinen模型:

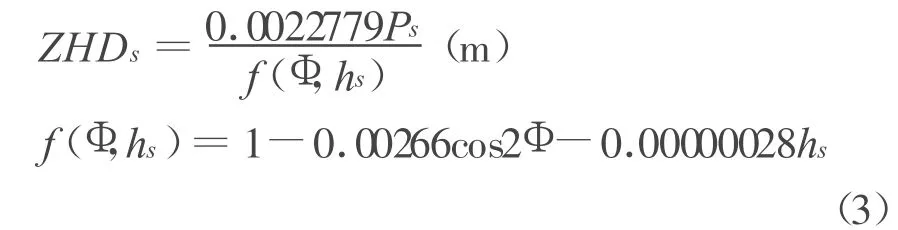
式中:Ps为测站地面气压(hpa);Ts为测站绝对温度(K);hd为中性大气层顶部高于大地水准面的有效高度(m);hs为测站大地高(m);Φ为GPS接收站纬度。

由以上公式可知,Hopfield模型适用于已知中性大气层高程的情况,与测站温度有关;Saastamoinen模型适用于测站地面温度未知的情况,要求已知站点坐标;Black不需考虑站点坐标,但需要测站温度。选择此三种静力学延迟模型进行内符合情况和外符合情况的分析,力求得到最适于四川地区的ZHD的计算模型。

1.1 三种模型的内符合情况

模型的内符合情况是指根据相同的外部因素(坐标、气压、温度),利用三种模型分别计算ZHD,用相关系数、平均偏差和偏差标准差来分析模型之间的相符性。可以认为,与多数模型结果有较大偏差的模型在该地区的适用性较差。

根据2008年YBIN(宜宾)站地面实测气象数据(温度、气压)计算三种模型的Z HD,列出1月、7月三种模型的Z HD比较图,如图1、2所示,全年各项指标如表1所示。

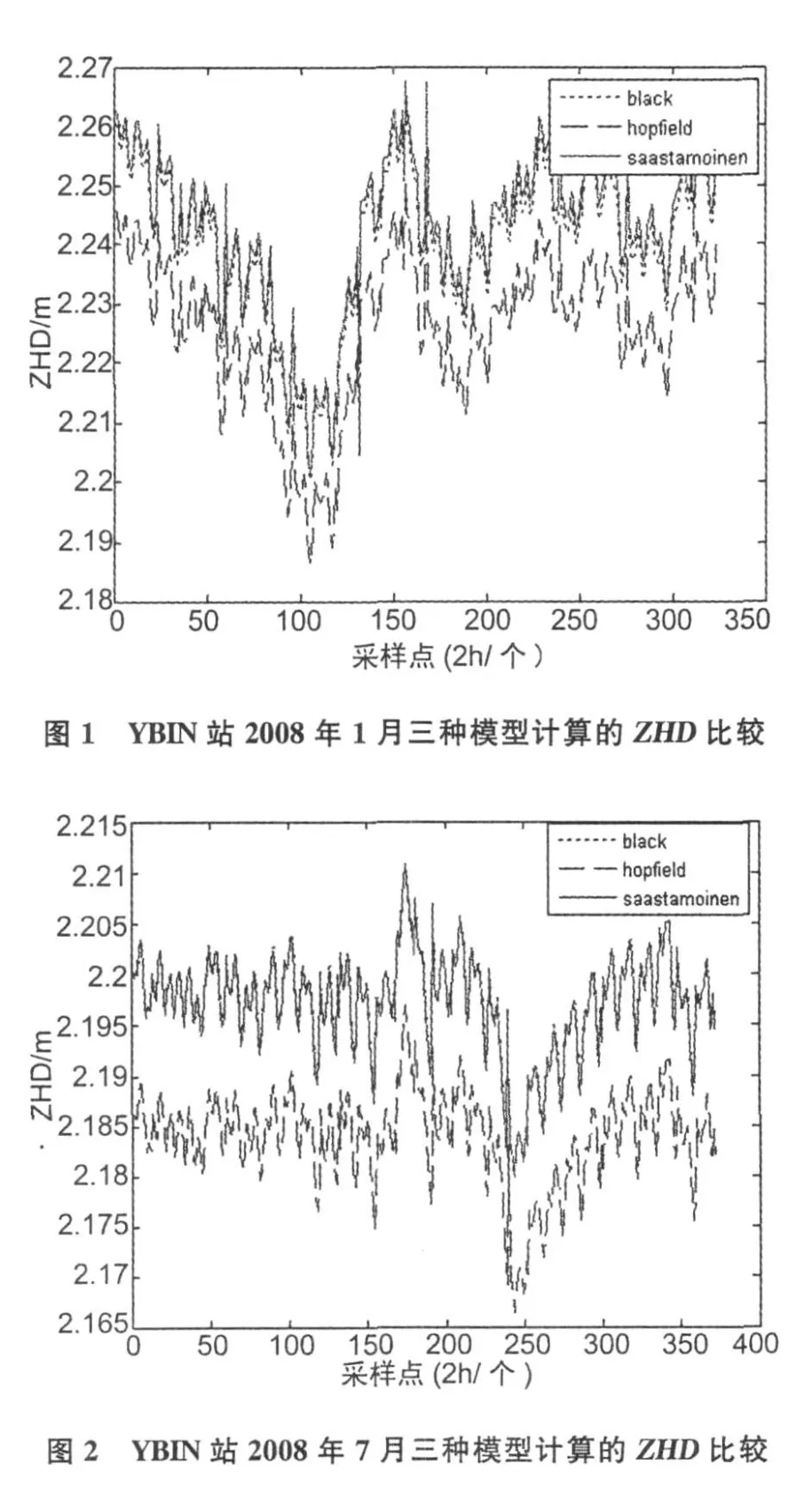
表1 YBIN站2008年三种模型计算的ZHD的比较

由上面的图表可见,三种模型计算的Z HD变化趋势一致,Black和Saastamoinen模型的结果较接近,Hopfield有较大偏差。

1.2 三种模型的外符合情况

模型的外符合情况是指根据相同的外部因素(坐标、气压、温度、ZTD、加权平均温度公式),利用三种模型经过水汽反演得到的GPS-PWV与探空气球的可降水量(RS-PWV)进行比较,分析GPSPWV与RS-PWV的符合程度。很显然,与RSPWV结果更接近的模型,更适于该地区。

利用三种Z HD模型和Bevis经验回归公式水汽反演得到的GPS-PWV与RS-PWV进行比较,只列出1月、7月三种模型计算的GPS-PWV与RS-PWV的比较图,如图3、4所示,全年指标如表2所示。

表2 YBIN站2008年三种模型计算的GPS-PWV与RS-PWV的比较

由上面图表可见,三种模型的GPS-PWV与RS-PWV比较,总体趋势一致。Hopfield的PWV比 RS-PWV平均偏大,Saastamoinen和Black的PWV比RS-PWV平均偏小,三种模型的离散程度相当。同时考虑到四川网站点坐标已知,因此Saastamoinen模型更适合,因此,我们选择Saastamoinen模型作为四川网解算的天顶静力学延迟模型。

2 Tm的计算

将天顶湿延迟ZWD转化为GPS-PWV,需要转换系数Π,而Π又是由加权平均温度 Tm决定的,因此Tm是计算高精度GPS-PWV的关键。目前,Tm的估计方法主要有五种:常数法、近似积分法、探空资料数值积分法、利用数值预报值计算以及Bevis经验公式。探空资料数值积分法是最为精确的方法,但该方法需要较多参数,计算复杂且时间分辨率低。现在的学者们多使用探空资料数值积分法计算 Tm值,然后与地表温度Ts进行回归分析,建立类似于Bevis经验公式的局部加权平均温度公式[14,16]。使用同样的方法,通过2007年YBIN站的探空数据回归出四川加权平均温度的计算公式,这里简称SC公式:

经过计算,SC公式计算 Tm的均方差为1.95 K,满足水汽反演要求的 Tm的均方差小于3.4 K的要求。为了进一步说明SC公式的可行性,本文使用SC公式计算了GPS-PWV并与RSPWV进行比较,相关系数为0.95、平均偏差为-1.10 mm、偏差标准差为4.91 mm,基本满足水汽反演的要求,如图5所示。

3.1 原料准备。第一步是备料，把日常生活中廉价而易得的布头、废旧衣服(以纯棉布最好)拆洗干净，裁剪成大小适当的尺寸。第二步是做“褙子”，即用刷子在布料上涂刷自制的面粉浆糊，将布料逐层裱糊在一起。第三步是剪样，用硬纸板画出各种尺码鞋垫的大小，拓在“褙子”上，先用铅笔画个样，再用剪刀裁下模子。第四步是搭面，用糨糊在裁好的模子上贴一层新的白棉布，作为鞋垫上纳绣图案的“面子”。这样，鞋垫的“骨子”就做好了。

3 GPT气象数据

目前,许多GPS网络的站点没有安装气象观测装置,但是地表温度和气压在水汽反演中不可或缺,因此使用GPT模型(全球气压和温度模型)来估计站点的地表温度和气压,得到GPT模型下的可降水量,并通过与实测气象PWV、RS-PWV的比较,以及降水预报情况分析,说明GPT模型的可行性。

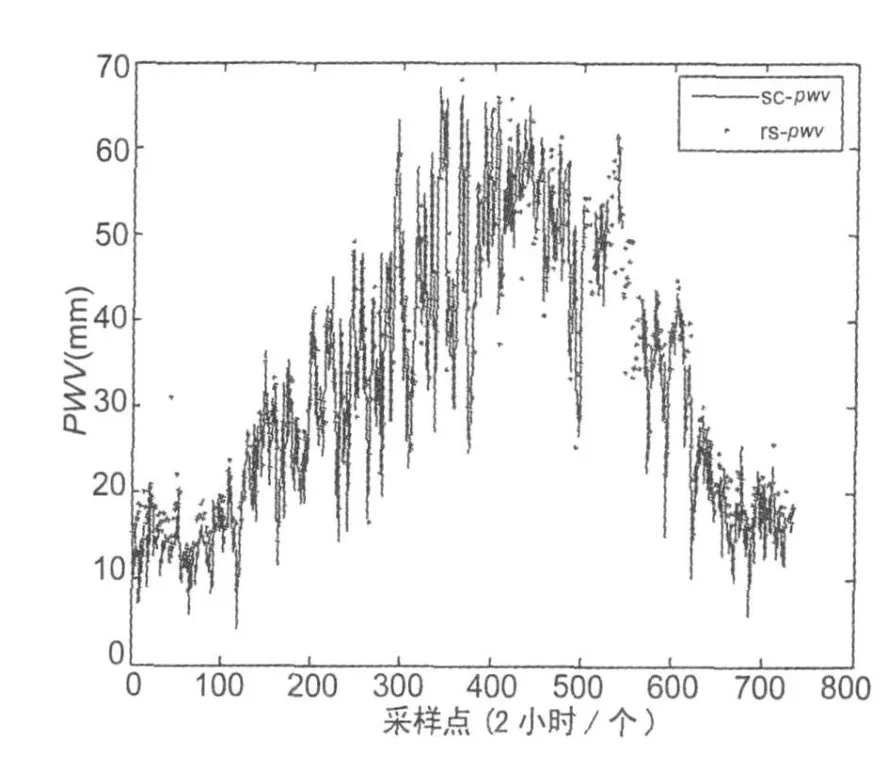
图5 通过SC公式计算的2008年YBIN站GPS-PWV与RS-PWV的比较

3.1 GPT-PWV、实测气象-PWV与RS-PWV的比较

分别使用GPT气象数据、实测气象数据,根据Saastamoinen静力学延迟模型与SC公式计算出了GPT-PWV和实测气象-PWV,并与RSPWV进行比较。如图6、表3所示。

由图 6、表3可见,GPT-PWV、实测气象-PWV以及 RS-PWV变化趋势一致。在数值上GPT-PWV的质量比实测气象-PWV质量稍差,GPT-PWV、实测气象-PWV分别与RS-PWV的平均偏差和偏差标准差较接近,但两者在个别时刻都与RS-PWV偏离较多,分析原因如下:

图6 YBIN站2008年GPT-PWV、实测气象-PWV、探空-PWV比较图

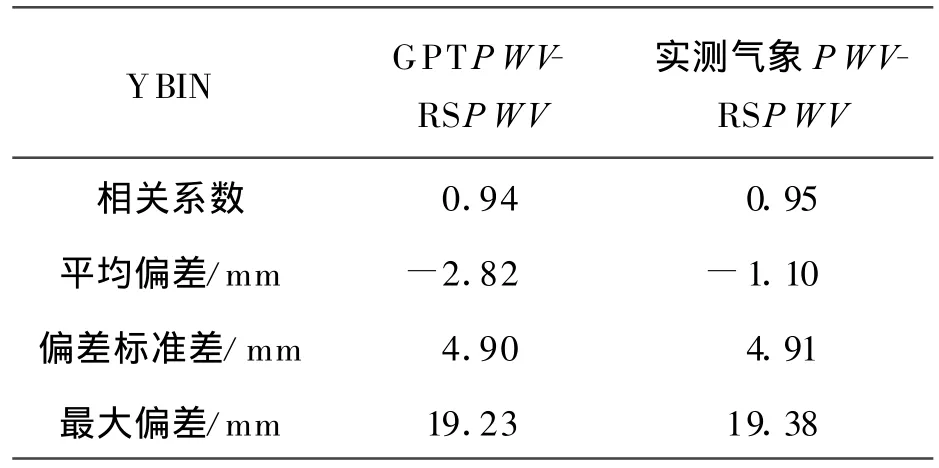
表3 YBIN站2008年GPT-PWV、实测气象-PWV分别与RS-PWV的比较

1)探空气球使用的是地面到探空上界各个标准层数据来计算的,含有模型误差。

2)水汽主要存在于底层大气,底层探空层次资料稀少影响了探空水汽精度。

3)GPS-PWV与RS-PWV两种计算PWV的方法反映的时间空间情况不同。GPS反演的水汽代表某个仰角到天顶方向的平均水汽总量,且可以全天连续观测。而探空资料反映的是气球随风飘曳路径上的水汽情况,每天只放两次气球。

可见,使用探空气球计算的PWV作为基准并不准确,如有条件,水汽辐射计可以提供更为精确的结果。

3.2 GPT-PWV、实测气象-PWV降水预报

为了从数值上说明GPT-PWV、实测气象-PWV与实际降水的关系,本文对李炳华和黎守德提出的GPS-PWV偏离系数PWV*的概念[17]进行了改进。PWV*计算公式如下:

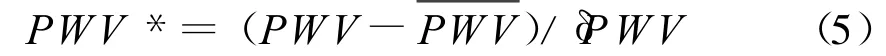
通过对GPT-PWV的偏离系数、实测气象-PWV的偏离系数与实际降水量的对比分析得出了一些结论:

1)通常偏离系数＞=1之后不久会产生降水。

2)偏离系数一直保持在1以上,说明水汽含量总是保持在较大的水平上,发生强降雨的可能性较大,也有可能连续降雨。

3)GPT-PWV与实测气象-PWV的偏离系数曲线变化趋势一致,偶尔有些差距,但对于降水的预报没有产生太大的影响。如图7～图10、表4所示。

图10 YBIN站2008年8月4日-8月11日GPT-PWV、实测气象-PWV与实际降水量的对比

表4 GPT-PWV与实测气象-PWV的偏离系数对于降水的预报情况

4 结 论

1)通过内符合情况和外符合情况的分析,以及考虑四川网络特点,确定Saastamoinen模型较适合于四川地区。

2)利用2007年YBIN站探空资料回归分析出四川加权平均温度计算公式,并说明此公式在四川地区的有效性。

3)使用GPT模型代替实测气象数据得到可降水量信息,通过与实测气象数据的PWV、探空PWV以及实际降水的比较,说明了GPT模型在缺少实测气象数据时可以使用,对于降水预报没有太大影响。

[1] Askne J,Nordius H.Estimation of tropospheric delay for microwaves from surface weather data[J].Radio Sci.,1987,22(3):379-386.

[2] Bevis M,Businger S,Herring T,et al.GPS meteorology:remote sensing of atmospheric water vapor using the global positioning system[J].J Geophys Res.,1992,97(D14):15787-15801.

[3] Rocken C,Hovr T,Johnson J,et al.GPS/STORMGPS sensing of atmospheric water vapor for meteorology[J].Journal of Atmospheric and Oceanic Technology,1995,12(3):468-478.

[4] Duan J P,Bevis M,Fang D,et al.GPS meteorology:direct estimation of the absolute value of precipitable water[J].Journal of Application Meteorology,1996,35(6):830-838.

[5] Ohtani R,Natio I.Comparisons of GPS-derived precipitable water vapors with radiosonde observations in Japan[J].Geophys.Res.Lett,2000,105(26):917-926.

[6] Gendt G,Dich G,Reigber C,et al.Near real time GPS water vapor monitoring for numerical weather prediction in Germany[J].Meteor.Sor.Japan,2004,82(1B):361-370.

[7] Stoew B,Elgered G.Characterization of atmospheric parameters using a ground based GPS network in north Europe[J].Meteor.Soc.,Japan,2004,82(1B):587-596.

[8] 王小亚,朱文耀,丁金才,严豪健.上海地区GPS/STORM试验与结果[J].全球定位系统,2000,25(3):6-10.

[9] 谢 璞,张胡大,王迎春,等.北京地区单双频地基GPS大气水汽遥测试验与研究[J].应用气象学报,2006,17(Z1):28-33.

[10] 陈永奇,刘焱雄,王晓亚,李品华.香港实时GPS水汽监测系统的若干关键技术[J].测绘学报,2007,36(1):9-12.

[11] 李建国,毛节泰,李成才,夏 青.使用全球定位系统遥感水汽分布原理和中国东部地区加权“平均温度”的回归分析[J].气象学报,1999,57(3):283-292.

[12] 杜瑞林,乔学军,王 琪,等.用地基GPS资料分析大气可降水汽总量[J].大地测量与地球动力学,2005,25(3):121-124.

[13] 李国平.地基GPS遥感大气可降水量及其在气象中的应用研究[D].成都:西南交通大学,2007:1-195.

[14] 吕弋培,殷海涛,黄丁发,王续本.成都地区大气平均温度建模及其在GPS/PWV计算中的应用研究[J].测绘科学,2008,33(4):103-105.

[15] 刘焱雄、陈永奇.GPS气象学中垂直干分量延时的精确确定[J].测绘学报,2000,29(2):172-179.

[16] 谷晓平,王长耀,吴登秀,等.GPS水汽遥感中的大气加权平均温度的变化特征及局地算式研究[J].气象科学,2005,25(1):79-83.

[17] 李炳华,黎守德.全球卫星定位系统(GPS)水汽资料在暴雨临近预报中的发展和应用[R].第十九届粤港澳气象科技研讨会,2005.