基于LabVIEW的风电机组滚动轴承故障诊断系统及其仿真

徐浩凇，郑小霞

（上海电力学院电力与自动化工程学院，上海 200090）

滚动轴承是风力发电机组的关键部件之一，其中最重要的齿轮箱滚动轴承和发电机滚动轴承都属于经常发生故障的部件［1］.因此，研究滚动轴承的故障诊断对风电机组正常运行具有重要意义.

由于伴随轴承故障的发生、发展，往往会引起信号频率结构的变化，而根据此时的频率可判断轴承是否发生故障，并可以此确定故障类型.因此频域分析是轴承故障诊断的有效方法.文献［2］采用LabvieW设计的软件平台在时域和频域内对轴承振动信号进行了故障诊断，但其频域分析采用依赖硬件参数的共振解调方法，这使得LabvieW参数设置较为复杂.

本文采用基于特征参数的滚动轴承故障诊断方法，依据振动信号的峭度指标、峰值因数、偏态因数等参数对滚动轴承的内圈、外圈、滚动体进行故障识别，并提出了希尔伯特包络谱分析的滚动轴承故障诊断方法，该方法在小波变换求得高频系数的基础上，用希尔伯特变换求取振动信号的包络谱，从而确定轴承的故障类型.在LabVIEW 8.5环境下开发了基于特征参数和希尔伯特包络谱分析法的风电机组滚动轴承故障诊断系统.故障诊断实验结果表明，该系统能够有效、快速、准确地对滚动轴承内圈、外圈、滚动体故障进行识别并报警.

1 基于特征参数滚动轴承故障诊断

对于一个有损伤的轴承，当滚动体接触点进入缺陷区时，就会发生机械冲击，冲击脉冲幅度与损伤程度成正比.由于冲击力的变动幅度很大，且带有较大的随机噪音，因此，用波形特征参数来表示冲击波形幅度能有效反映轴承的故障状态，这是轴承故障检测中的常用方法［3］.

由于滚动轴承振动信号是随机的，其本身不能直观地反映系统状态的变化，但通过统计分析，可以找到反映其统计规律的特征量.在信号的幅值上进行各种处理，即对信号的时域进行统计分析称为幅域分析.幅域统计方法计算简单、显示直观、容易理解，在简易振动诊断中应用非常广泛.常用的信号幅域统计参数包括有效值、峭度、峰值因数、偏态指标、峭度指标、裕度因数、脉冲因数、峰态因数等.

2 基于希尔伯特包络谱分析的滚动轴承故障诊断

由于滚动轴承振动信号的不平稳特性，合理地选择信号处理方法对于确保故障诊断系统的精确性很重要.不准确的信号分析会导致故障诊断系统多次错误报警，降低故障诊断的准确性［4］.

小波分析具有对信号的自适应性，能识别振动信号的突变成分;振动信号经希尔伯特变换后得到其包络谱，由包络谱获得故障特征信息.由此可结合小波分析和希尔伯特变换二者的优点对轴承进行故障诊断.

2.1 滚动轴承特征频率

滚动轴承的异常振动频率由转子的旋转速度、损伤部位的形态，以及轴承元件的固有振动频率所决定.转子的旋转速度越高、损伤越严重，其振动频率就越高.滚动轴承故障的振动特征是：当发生异常时，频谱丰富，不会只产生单一的特定频率，各频率分量的幅值显著增大.由于轴承元件的固有频率较高，通常在1×103～1×104Hz内，一旦某种元件出现异常激发该种固有频率，频谱中就会出现高频成分.因此，利用轴承元件的固有频率诊断故障是一种有效的方法［4］.

由于结构、运行特性不同，各零部件有不同的特征频率.滚动轴承的特征频率（即接触激发的基频）可以根据轴承元件之间滚动接触的速度关系所建立的方程求得.用它计算的特征频率值往往十分接近测量数值，因此在诊断前总是将其先计算出来，并以此作为诊断的依据.对于外圈固定的轴承，可运用下列公式计算出各元件的故障特征频率.

内圈（外滚道）缺陷频率为：

2.2 小波变换

对非平稳信号进行分析时，高频信号需要采用小时间窗，而低频信号需要采用大时间窗，即窗口大小应随频率变化而改变，但加窗傅立叶变换无法实现这一功能.小波分析是一种窗口大小固定但其时频窗可以改变的时频局部化分析方法，在低频部分具有较高的频率分辨率和较低的时间分辨率，在高频部分具有较高的时间分辨率和较低的频率分辨率.正是这种特性，使小波分析具有对信号的自适应性，能识别振动信号的突变成分［5］.

小波变换的基本思想与傅里叶变换是一致的，它也是用一族函数去表示信号或函数，这一族函数称之为小波函数系.小波函数系是由一基本小波函数的平移和伸缩构成的.与傅里叶变换相比，小波变换是时间（空间）频率的局部化分析，它通过伸缩平移运算对信号（函数）逐步进行多尺度细化，最终达到高频处时间细分，低频处频率细分，能自动适应时频信号分析的要求，从而可聚焦到信号的任意细节，解决了傅里叶变换中存在的难题.有人把小波变换称为“数学显微镜”.

小波定义过程如下.

对于任意ψ（t）∈L2（R），即ψ（t）是平方可积函数，如果ψ（t）的傅里叶变换满足可容许条件：

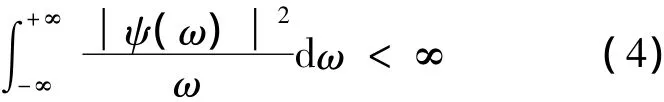
则称ψ（t）是一个基本小波或母小波函数.

在多数情况下，要求ψ（t）连续且有一个矩为零的大整数M，也即对所有整数m＜M，有：

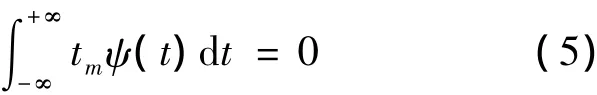
这表示母小波必须非零且均值为零.

母小波ψ（t）缩放（或称膨胀）α倍并平移b得到：

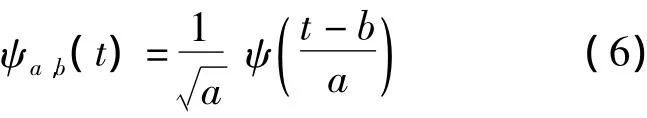
人们称ψa，b（t）为小波基函数，也称小波.它是由一个母小波函数经过伸缩与平移所产生的二维空间的基底，依赖于参数a和b.其中a被称为尺度因子（参数），b被称为时移因子（参数）.尺度参数a改变小波的形状，时移参数b改变小波的位移.

2.3 希尔伯特包络谱

轴承的许多故障信息是以调制的形式存在于所监测的振动信号之中，如果借助希尔伯特变换对这些信号进行解调处理，就能方便地获得故障特征信息，以确定轴承所发生的故障类别.希尔伯特谱是信号的幅值随时间和频率变化的精确描述［5］.包络分析的宽频带特性常引起系统固有频率处的谐振，从而在该频率附近形成以特征故障频率为基频的边带，此边带是故障信号调制的结果，因此包络分析又称为解调分析.通过对包络信号进行频率分析，能比较精确地确定故障发生的部位和层次.

希尔伯特解包络的原理就是让测试信号产生一个90°的相移，从而与原信号构成一个解析信号，求出的解析信号就构成了包络.希尔伯特解包络的原理如图1所示.

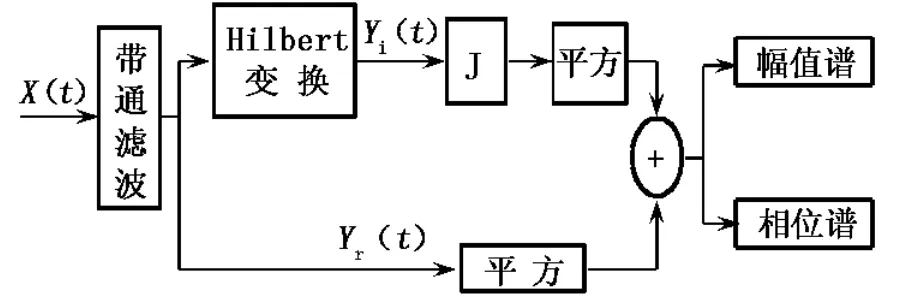
图1 希尔伯特解包络原理

X（t）为振动加速度信号，带通滤波后得到信号yr（t），yr（t）经过希尔伯特变换后得到信号yi（t），二者构成解析函数式Z（t），即：

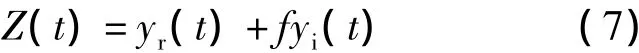
由此得到振动信号的幅值调制信号为：

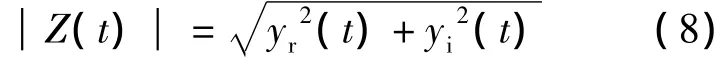
上述过程完成了对信号的解包络分析.

3 基于LabVIEW的风电机组滚动轴承故障诊断系统的开发

LabVIEW是美国国家仪器（NI）公司推出的使用最为广泛的虚拟仪器计算机语言.在特征参数故障诊断和希尔伯特包络谱分析故障诊断的基础上，利用LabVIEW平台建立了风电机组滚动轴承故障诊断系统，主要包括振动信号的数据处理模块、故障诊断模块、数据存储模块、系统时间模块，以及显示面板等部分，总体结构如图2所示.

基于LabVIEW的风电机组滚动轴承故障诊断系统的程序示意如图3所示.

LabVIEW很重要的一个优势就是界面编辑的所见即所得.用其构建的显示面板形象生动，布局灵活性强.基于LabVIEW的风电机组滚动轴承故障诊断系统前面板如图4所示.

由图4可知，该系统实现了故障报警、波形显示、特征参数显示、特征频率显示、故障部位显示、保存数据、系统时间显示和希尔伯特包络谱显示等功能.

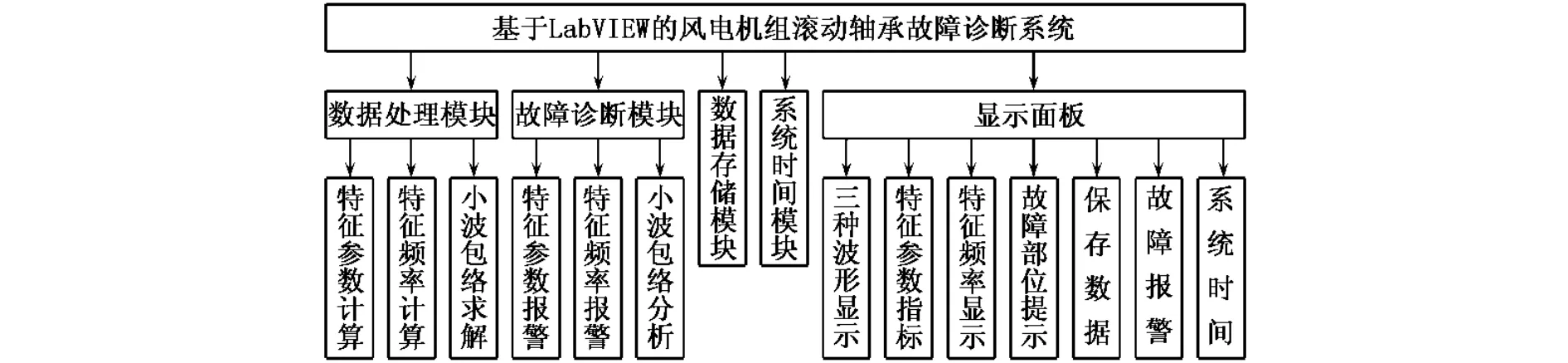
图2 基于LabVIEW的风电机组滚动轴承故障诊断系统的功能模块

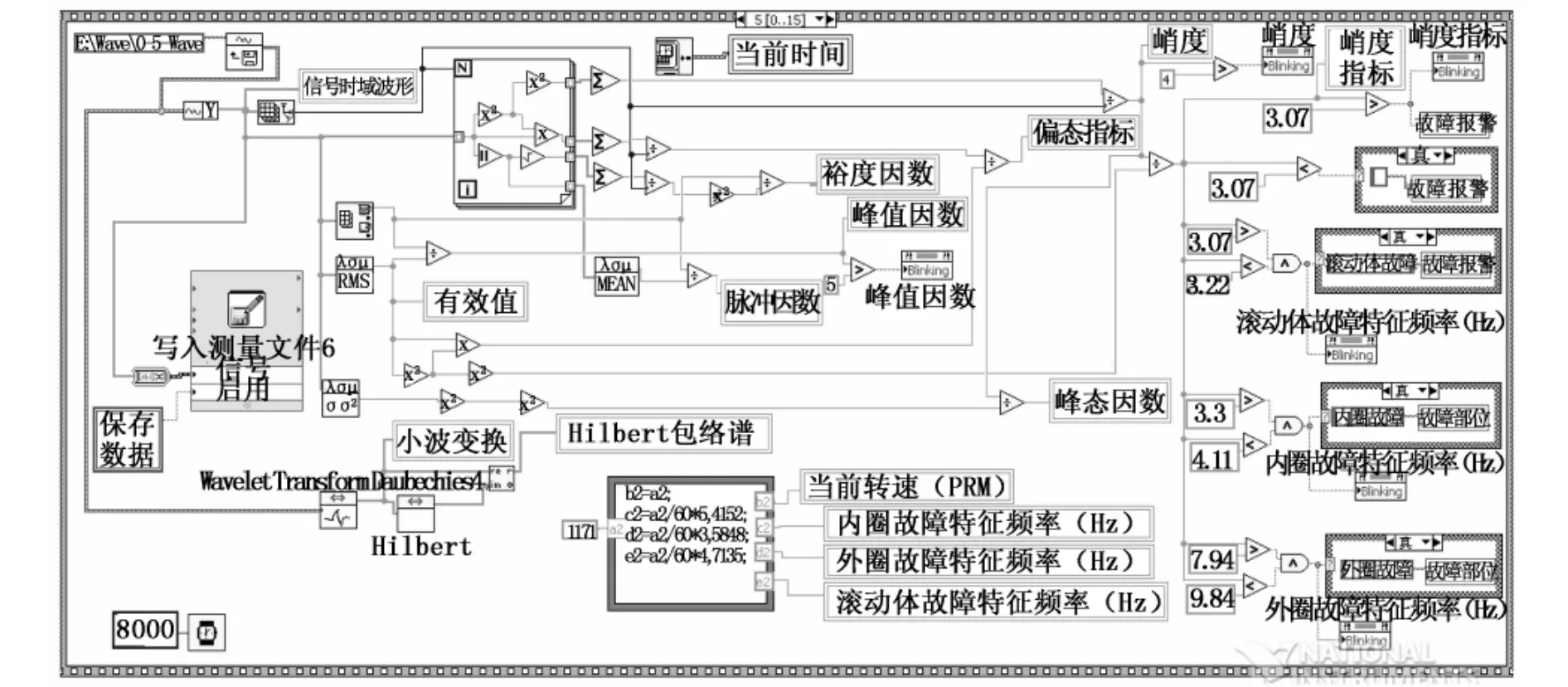
图3 基于LabVIEW的风电机组滚动轴承故障诊断系统的程序示意

4 故障诊断系统仿真研究

故障诊断仿真实验采用美国凯斯西储大学（CWRU）轴承数据中心的滚动轴承故障数据（http：//www.eecs.cwru.edu/laboratory/bearing）.本次实验数据选取滚动轴承驱动端在746 W的电机负载下，外圈故障点的方向与负载区方向垂直，轴承转速1 771～1 797 r/min，采样频率为48 000 Hz，通过放电加工（Elecctric Discharge Machining，EDM）技术，在内滚道、外滚道和滚动体上人为制造的直径0.533 4 mm，深度为0.279 4 mm的轴承故障.采样序列数据长度为1 024点，振动信号由与磁性基座相连的加速度传感器获取.

由于篇幅限制，本文仅以轴承外圈故障的诊断为例.选取轴转频fs=29.5 Hz，采样序列长度为1 024点的外圈故障数据.外圈故障特征频率计算经验公式为：fo=3.584 8×fs，将fs=29.5 Hz代入公式，得fo=105.8 Hz.

利用该故障诊断系统对滚动轴承外圈故障诊断结果如图5所示.

从图5中可直观地看出，故障报警灯呈报警状态的同时，峭度指标为8.89且闪烁提示，外圈故障特征频率值为105.81 Hz并闪烁提示;故障部位提示区醒目显示：外圈故障;从信号时域波形图上可以看出此时冲击较为强烈，小波变换所得的高频系数呈离散状分布，且冲击很强，希尔伯特包络谱最大脉冲对应频率105 Hz和210 Hz正是轴承外圈故障特征频率和其2倍频，由此频率也可推断轴承外圈出现故障.

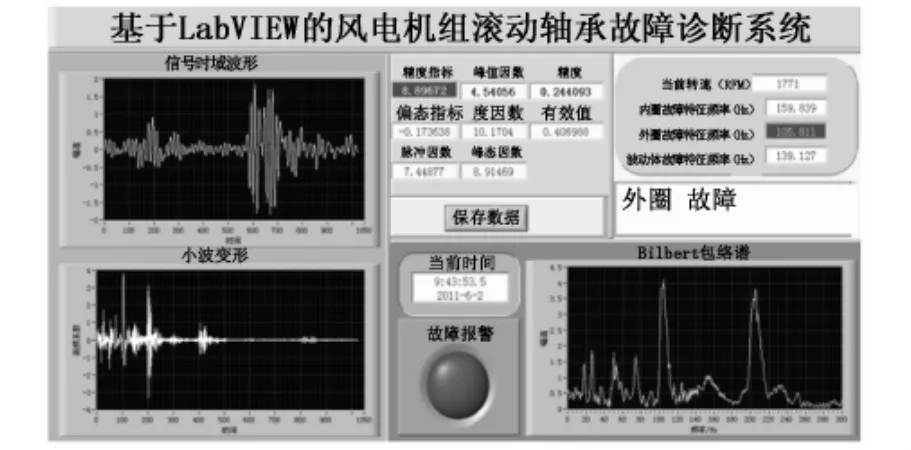
图5 滚动轴承外圈故障诊断结果

5 结语

本文在LabVIEW 8.5环境下实现了基于振动信号特征参数和希尔伯特包络谱分析的两种故障诊断方法，开发了风电机组滚动轴承故障诊断系统.该系统的前面板形象生动，实现了故障自动报警、故障类型显示、特征频率显示闪烁报警、希尔伯特包络谱显示，以及数据存储等功能.故障诊断实验结果表明该系统可以直观、准确、迅速地诊断出滚动轴承外圈、内圈、滚动体的故障.

［1］任腊春，张礼达.基于模糊理论的风力机故障诊断专家系统的研究［J］.流体传动与控制，2009（6）：10-12.

［2］苏敏，王勇，何惜港.基于LabVIEW的滚动轴承故障诊断系统［J］.轴承，2010（9）：41-44.

［3］MCFADDEN P D，TOOZHY M M.Application of synchronous averaging to vibration monitoring of rolling element bearings［J］.Mechanical Systems and Signal Processing，2000，14 （6）：891-906.

［4］DANESHI Far D，CAPOLINO G A，HENAO H.Review of failures and condition monitoring in wind turbine generators［C］//XIX International Conference on Electrical Machines，2010，Rome，2010：1-6.

［5］赵玉菊，陈恩利，史振江.基于小波包络分析的滚动轴承故障诊断研究［J］.石家庄铁路职业技术学院学报，2009，8 （4）：36-41.

（编辑苏娟）