改进SFMEA的AUV风险评估方法

史长亭，张汝波

(哈尔滨工程大学 计算机科学与技术学院，黑龙江 哈尔滨 150001)

智能水下机器人(autonomous underwater vehicle，AUV)由于工作环境的复杂性﹑外界因素的未知多变性，使得任何细微的故障都有可能产生灾难性的后果，这也对水下机器人软件系统的可靠性提出了更高的要求［1］.因此，如何对水下机器人软件系统的失效模式进行有效分析，帮助准确定位机器人的失效原因和评价各种软件失效对系统造成的影响，从而提出针对性改进措施，进而提高水下机器人软件系统的可靠性与安全性将具有重要的意义.

软件失效模式影响分析(software failure modes and effects analysis，SFMEA)是对软件及软件所嵌入的系统进行的一种可靠性、安全性设计与分析方法［2-3］.但是传统失效模式影响分析(failure modes and effects，FMEA)，风险评估过程主要是通过计算风险顺序数(risk priority number，RPN)来评估产品或系统的风险等级［4-5］，其中RPN是发生率O、严重度S和难检度D三者的乘积.这样在由不同O、S、D相乘得到相同的RPN值的情况下，各种失效模式对于系统的风险作用并不相同［6］.另外，传统FMEA也很难对主观或定性的描述语言变量做出准确判断，这些都极大地限制了FMEA的使用效果.

针对传统FMEA存在的上述缺陷，Bowles和Antonio等人将模糊推理系统的方法技术应用到FMEA中［7］，Pillay等将灰色关联决策应用到FMEA的研究框架中［8］.门峰研究了基于模糊集理论和灰色关联理论的FMEA方法［9］.现有的方法都是只将O、S、D三者的值作为单值来处理，而在水下机器人实际系统中，由于任务的复杂性，机器人在执行不同的任务过程中，各失效模式发生的概率和难检度以及各失效模式对于任务的完成质量和系统的影响程度是不同的.在这种情况下，采用传统的FMEA和现有的FMEA方法都无法对失效模式风险评估结果进行有效的比较，进而确定风险排序.

本文从研究水下机器人软件系统失效模式风险定量评估方法的角度出发，在现有基于模糊分析方法的基础上，研究了基于灰色区间关联的SFMEA方法，试图在水下机器人软件系统中对失效模式风险进行定量评估，使风险的评估更加接近实际情况.

1 基于模糊分析和灰色区间关联的SFMEA风险评估方法

1.1 基于三角模糊数的FMEA评价模型

将水下机器人各种失效模式的O、S、D 3个变量作为模糊语言变量，每个语言变量包含7种评价语言术语，即{极低(VL)，低(L)，较低(AL)，一般(M)，较高(AH)，高(H)，很高(VH)}.

在确定了水下机器人软件系统主要的失效模式、失效原因的基础上，由从事水下机器人软件测试及故障诊断的工作人员、科研人员组成专家小组来确定主要失效模式的模糊评价语言术语集及其对应的模糊数.

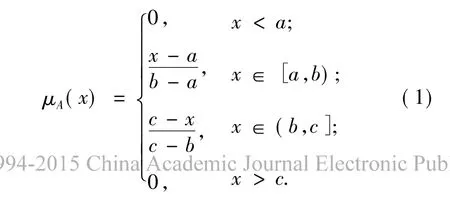
模糊数的形式有多种，本文采用三角模糊数［10］对模糊语言术语进行定量化处理.若模糊数A可由(a，b，c)决定，且隶属函数值为则称A为三角模糊数，记A=(a，b，c)，当a=b=c时，A为一个精确数.这样，模糊语言术语对应的三角模糊数，可以借助专家的知识和经验来确定.

模糊数的清晰化算法有多种［11］，本文根据三角模糊数分布特点，由

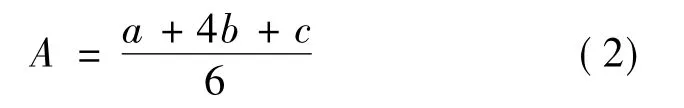
将三角模糊数(a，b，c)化为单值，即可得出最终的非模糊化评价结果，如表1所示.

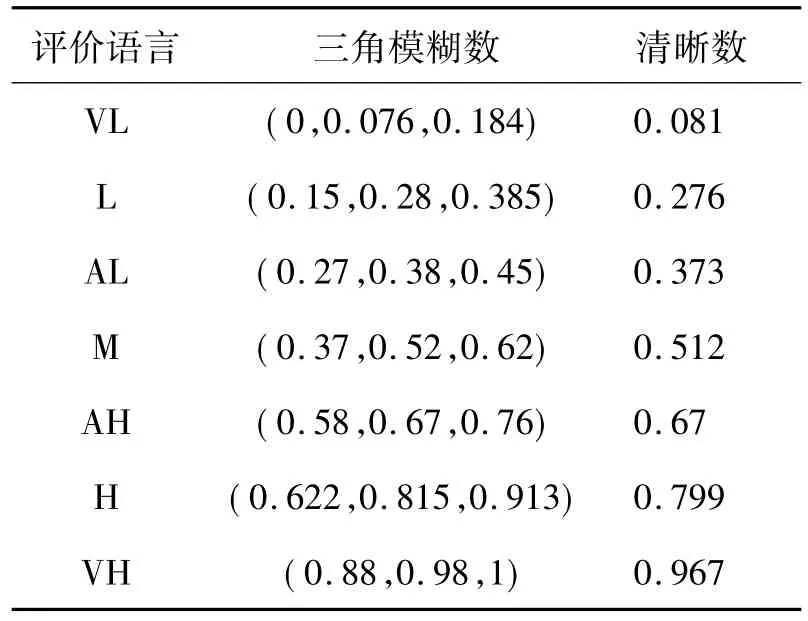
表1 模糊语言术语的清晰化Table 1 Clear value of fuzzy numbers

O、S、D可以采用相同的模糊语言术语集和模糊数，这样建立了模糊语言对应的模糊数，就可以对水下机器人主要失效模式做出评价.

1.2 基于灰色区间关联的失效模式风险排序

灰色关联分析是用关联度大小来描述事物之间、因素之间关联程度的一种定量化的方法.它以系统的定性分析为前提、定量分析为依据，进行系统因素之间、系统行为之间曲线相似性的关联分析［12］.

设失效模式评估对象集合U={1，2，…，n}，属性集合A={A1，A2，…，Am}，⊗表示灰数，则评估对象i在属性Aj下的量化评估值为非负区间型灰数…，m)，评估对象i的量化评估向量记为ui(⊗)= (ui1(⊗)，ui2(⊗)，…，uim(⊗))，(i=1，2，…，n).从而由上面的定义得到的灰色信息表G=(U，A).

为了消去量纲及数量级的影响以增加可比性，利用灰色极差变换对ui(⊗)进行规范化处理:

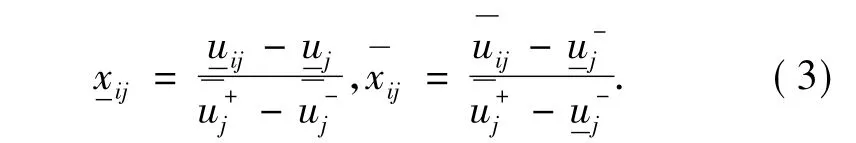
设规范化处理后的标准化评估向量为

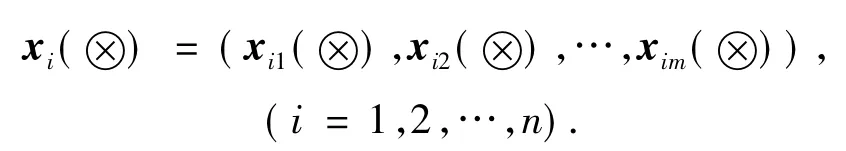
利用公式

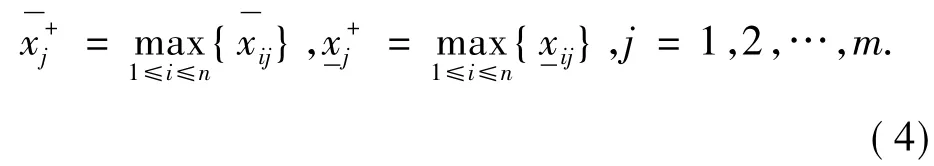
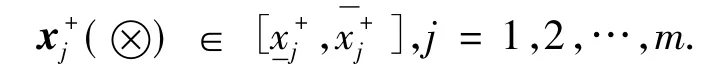
如上所述，则称

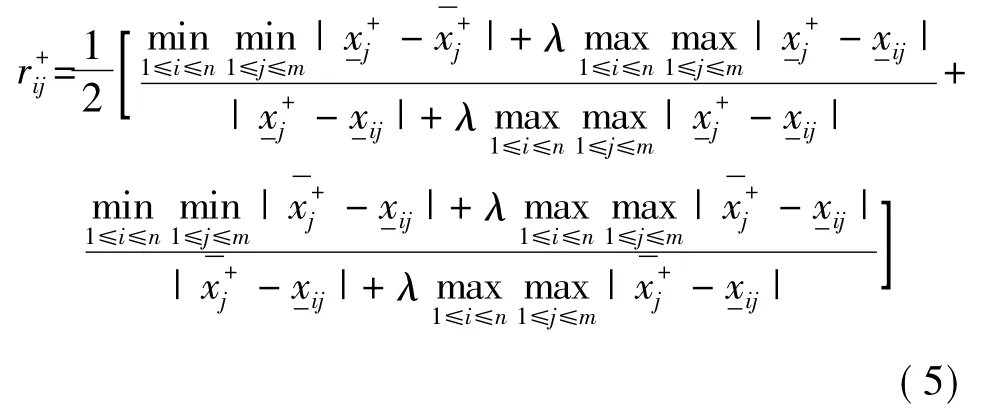
为子因素xij(⊗)(i=1，2，…，n;j=1，2，…，m)关于理想因素的灰色区间关联系数，其中λ∈［0，1］为分辨系数.并称1，2，…，n)为各评估对象关于理想对象的多属性灰色关联系数向量，矩阵为各评估对象关于理想对象的灰色区间关联系数矩阵.

关联系数所反应的是2个被比较序列之间的紧密程度，但关联系数所提供的信息过于分散，不便于比较，为此，这里将关联系数加权集中得到加权关联度:

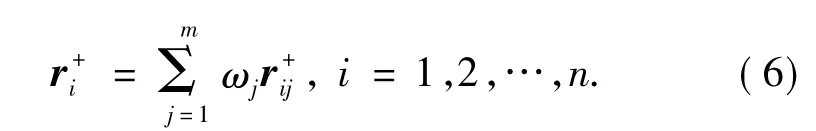
式中，ωj为属性Aj的权系数.

由公式

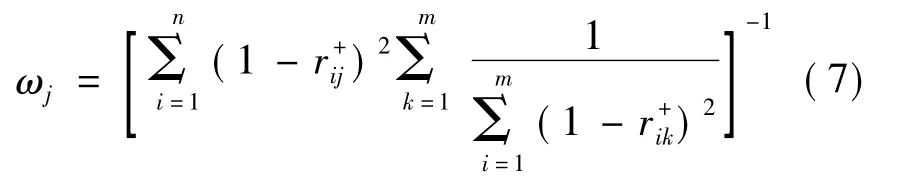
来计算以理想对象为参照标准时的属性权重向量ω=(ω1，ω2，…，ωm)，其中j=1，2，…，m.

这样可以由式(6)计算得到各失效模式评估对象关于理想评估对象的加权关联度，从而可以根据加权关联度数值的大小，通过排序来确定各失效模式的风险顺序.

2 AUV智能决策系统中的应用实例

本文以某AUV系统的智能决策子系统为分析对象，该系统主要包括6大功能模块:1)全局路径规划模块;2)局部路径规划模块;3)紧急情况处理模块;4)通讯模块;5)目标搜索模块;6)任务下达模块.以路径规划模块为例，其FMEA表如表2所示.

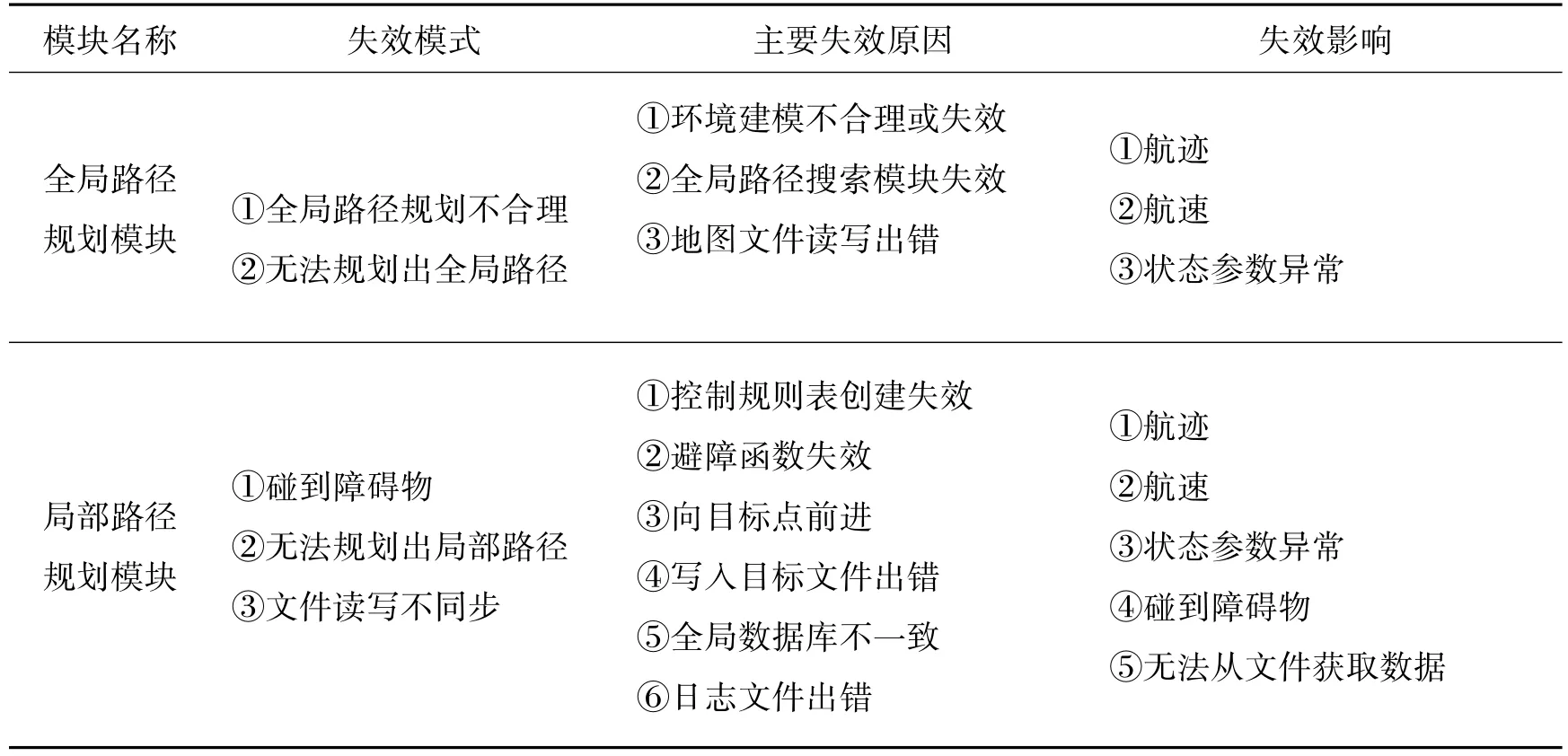
表2 路径规划模块FMEA表Table 2 FMEA table of path planning modules

本文从上述模块中选择了6种主要的失效模式，分别为1)全局路径规划不合理;2)避障失败;3)无法处理紧急情况;4)通讯超时;5)未能搜索到目标;6)任务没有顺利下达.这6种主要失效模式的模糊等级区间评价表如表3所示.

根据表1和表3，对失效模式集合关于属性集合A={O，S，D}进行量化评估，生成灰色信息如表4所示.

表3 失效模式模糊等级评价Table 3 Fuzzy rating variables of failure modes

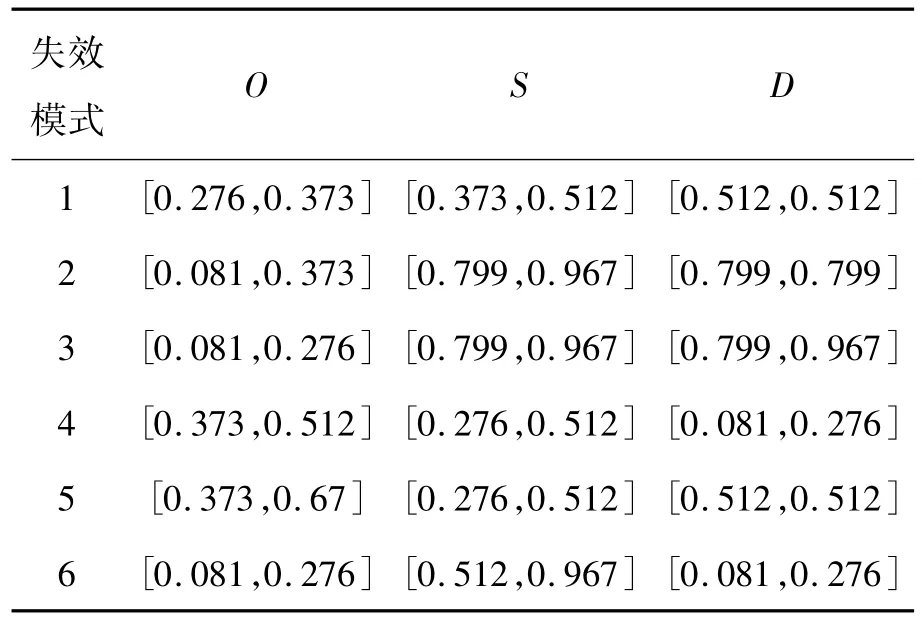
表4 失效模式量化评价灰色信息Table 4 Quantitative grey information of failure modes

利用灰色极差变换公式(3)对表4进行标准化处理，得到标准化的灰色信息如表5所示.

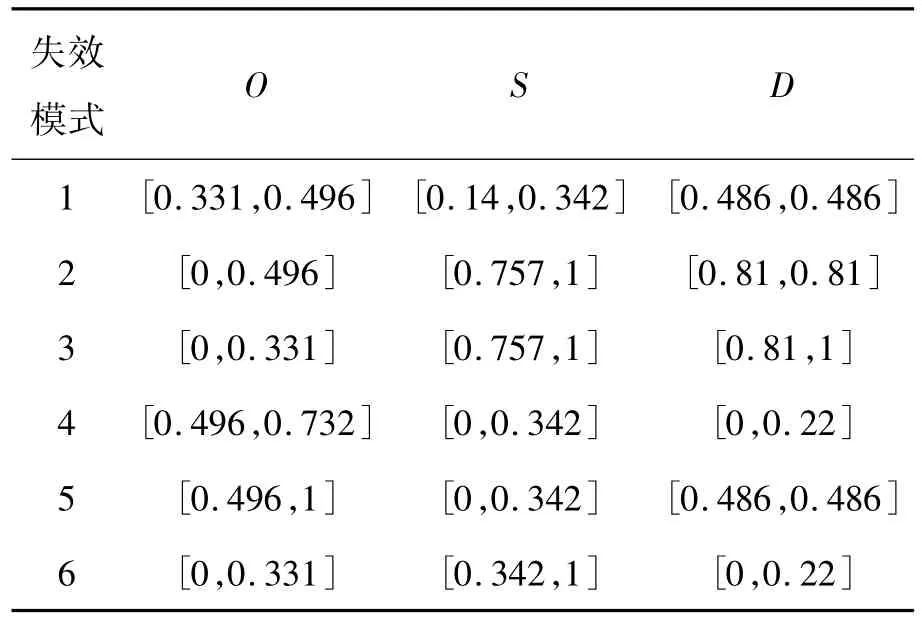
表5 失效模式量化评价标准化灰色信息Table 5 Standard quantitative grey information of failure modes

根据表5，利用式(4)得到理想对象评估向量: x+(⊗)=(［0.496，1］，［0.757，1］，［0.81，1］).

利用式(5)计算U中各对象关于理想对象的灰色区间关联系数，得到各失效模式对象关于理想对象的灰色区间关联系数矩阵(λ=0.5):

利用式(7)计算得到以理想对象为参照标准时的属性权重向量:

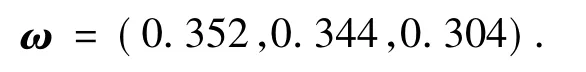
则根据式(6)可计算得到各失效模式评估对象关于理想评估对象的加权关联度:

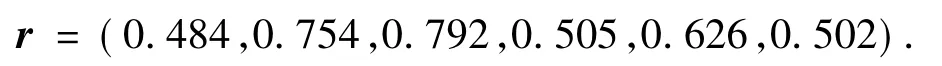
由于本文是以最差情况作为建立理想评估对象的标准，因此与其关联度越高，则说明该失效模式的风险越大.把所得到的水下机器人各失效模式加权关联度从大到小进行排序，就可以确定风险顺序，如表6所示.

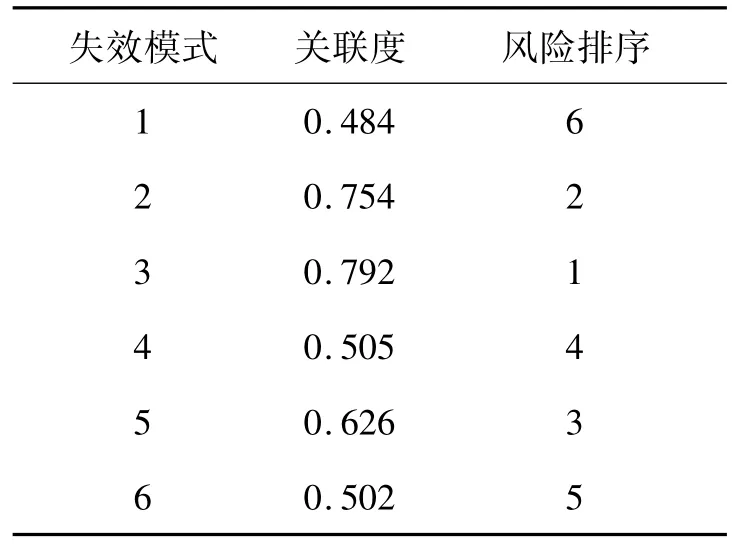
表6 基于灰色区间关联的风险排序Table 6 Risk priority rank based on grey region relation

由表6可以看出，失效模式3的风险最高，失效模式1的风险排序最小，这也与表4中的数据的实际意义相吻合.而如果采用传统的FMEA方法，所得到的RPN值将是一个区间数，使得各失效模式之间无法进行有效的风险比较，只能够先将O、S、D化为单值来处理，而这又具有一定的局限性，不符合系统的实际需求.由此可见，采用改进后的SFMEA方法，能够综合比较各潜在失效模式的风险作用，为智能水下机器人软件系统的设计、分析和改进提供依据.

3 结束语

对AUV智能决策子系统进行风险评估所得到的结果，证明了基于模糊分析和灰色区间关联的SFMEA风险评估方法的可行性.同现有的方法相比，本文所提出的方法有效地解决了传统FMEA方法的局限性以及O、S、D为区间数值的问题，使得风险评估过程更加符合系统的实际需求.

本文中的方法在选取基准评估向量的过程中，只是将与最优结果的比较情况作为理想评估向量，因此评价具有一定的片面性.如果能够综合考虑评估对象与正负理想基准评估对象之间的相互关系，那么评估结果将更加合理可信.这样将会对AUV软件系统的设计和使用具有更强的指导意义.

［1］徐玉如，庞永杰，甘永，孙玉山.智能水下机器人技术展望［J］.智能系统学报，2006，1(1):11-14.

XU Yuru，PANG Yongjie，GAN Yong，SUN Yushan.AUV—state-of-the-art and prospect［J］.CAAI Transactions on Intelligent Systems，2006，1(1):11-14.

［2］CHEN Zhi，FENG K M，ZHANG G S，YUAN T，PAN C H.Preliminary safety research for CH HCSB TBM based on FMEA method［J］.Fusion Engineering and Design，2008，83(5-6):743-746.

［3］吴邦国，唐任仲.软件FMEA技术研究［J］.机电工程，2004，21(3):8-12.

WU Bangguo，TANG Renzhong.Study on Software FMEA Techniques［J］.Mechanical＆Electrical Engineering Magazine，2004，21(3):8-12.

［4］BOWLES J B，PELAEZ C E.Fuzzy logic prioritization of failures in a system failure mode，effects and criticality analysis［J］.Reliability Engineering＆System Safety，1995，50(2):203-213.

［5］王高峰.FMEA在质量管理中的应用［J］.电子质量，2002 (11):60-63.

WANG Gaofeng.The application of FMEA in quality management［J］.Electronics Quality，2002(11):60-63.

［6］XU K，TANG L C，XIE M，HO S L，ZHU M L.Fuzzy assessment of FMEA for engine systems［J］.Reliability Engineering and System Safety，2002，75(1):17-29.

［7］ANTONIO C F.Effects analysis fuzzy inference system in nuclear problems using approximate reasoning［J］.Annals of Nuclear Energy，2004(31):107-115.

［8］PILLAY A，WANG Jin.Modified failure mode and effects analysis using approximate reasoning［J］.Reliability Engineering and System Safety，2003(79):69-85.

［9］门峰.模糊集理论与灰色关联理论的FMEA方法［J］.工业工程，2008，11(4):109-112，117.

MEN Feng.FMEA method based upon fuzzy set theory and grey relational theory［J］.Industrial Engineering，2008，11 (4):109-112，117.

［10］GUIMARAES A C F，LAPA C M F.Fuzzy inference to risk assessment on nuclear engineering systems［J］.Applied Soft Computing Journal，2007，7(1):17-28.

［11］CHANG Changliang，LIU Pinghung，WEI Chiuchi.Failure mode and effects analysis using grey theory［J］.Integrated Manufacturing Systems，2001，12(3):211-216.

［12］SHIH K C，WU K W.Information of grey relation［M］.Taiwan:Chuan-Hua Co Ltd，1996:3-8.