旋转叶片刚柔耦合系统动力学分析

韩广才，吴艳红，王寅超，刘志强

(1.哈尔滨工程大学 航天与建筑工程学院，黑龙江 哈尔滨 150001;2.哈尔滨工程大学 机电工程学院，黑龙江 哈尔滨150001)

随着汽轮机技术的发展，以及柔性多体系统动力学研究的深入，有关旋转叶片纵向、横向振动问题引起了众多学者的关注.将叶片视为弹性梁的研究可见诸于许多文献.Eringen等人［1］研究了无旋转运动弹性梁的非线性振动问题，Woodall等人［2］只考虑了梁的横向变形，推导出简化了的弹性梁动力学运动微分方程.Anderson等人［3］推导了旋转柔性梁的纵向和横向的非线性微分方程，Hodges等人［4］对于Anderson的方程进行了修正.Ansari等人［5］分析了安装在转盘上的预扭非均质非对称截面悬臂梁的非线性振动问题，表明在叶片稳态运动情况下，一个微小的扰动就会引起叶片的运动发生突变，且这种突变取决于扰动方向.2007年韩国Hong Seok Lim等人分析了集中质量冲击作用下旋转梁的振动问题，基于Kane方法推导了系统的动力学方程［6-7］.2007年台湾学者研究了盘的柔性对轴盘叶系统耦合振动的影响，文中讨论了轴的扭转、盘的横向振动及叶片的弯曲振动相互间的耦合关系［8］.

多年来准确预测经历大范围刚体运动和弹性变形的柔性叶片的动力学行为，始终是旋转叶片动力学问题研究的主要课题，基于线性理论的传统方法由于无法计及动力刚化效应，导致在许多实际应用中得到错误的结果.本文基于Hamilton原理建立了具有动力刚化效应的刚柔耦合旋转叶片动力学微分方程，考虑了变截面、预扭角叶片模型，计及了截面离心惯性力、截面转动和截面剪力等因素的影响，最后采用数值分析的方法通过算例分析了弹性体叶片端部振动位移响应.

1 动力学模型

如图1所示，将叶片视为一均质旋转铁摩辛柯梁，安装在半径为e的绕空间固定轴旋转的刚性圆盘上，考虑长度为L的双边楔形预扭叶片，设ρ为叶片单位体积的质量、E为杨氏模量，且宽度、厚度和截面扭转角沿叶片长度方向线性变化.叶片左端O点固定于半径为O1的刚性旋转圆盘上，Oz为刚性圆盘中心，轴为叶片未变形时中性轴.图1中，O1x1y1z1为惯性参考系，O1x'y'z'为固结于圆盘上的动参考系，绕惯性参考系O1y1轴以角速度Ω旋转，Oxyz为动参考系，固结在未变形的叶片上，随同叶片绕O1y1轴以角速度Ω旋转，作用于圆盘旋转平面内的力矩为τ，JD为刚性圆盘绕O1y1轴的转动惯量.P为叶片未变形时中性轴上的一点，由于旋转运动而发生了轴向变形及横向变形，对于细长叶片横向变形比轴向变形大得多，故只考虑横向变形，以z表示叶片未变形时P点位置，叶片变形后P至P'点，P点在动参考系Oxyz内的位移分别用w(z)和v(z)表示，w(z)为xz平面内的位移，v(z)是yz平面内的位移.变形后P点在O1x'y'z'动参考系内的位置可用rP表示为

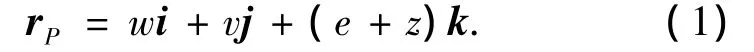
式中:i、j、k分别为动参考系O1x'y'z'沿坐标轴方向上的单位矢量，将式(1)在惯性参考系O1x1y1z1内求导，并注意到圆盘转动的角速度矢量为Ω=θ·j(θ为刚性圆盘转动角位移)，可得

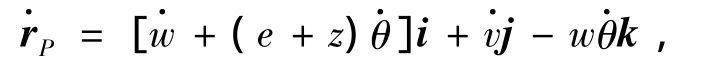
则

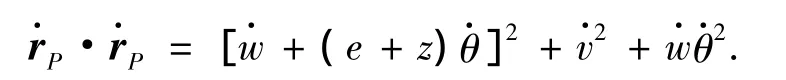
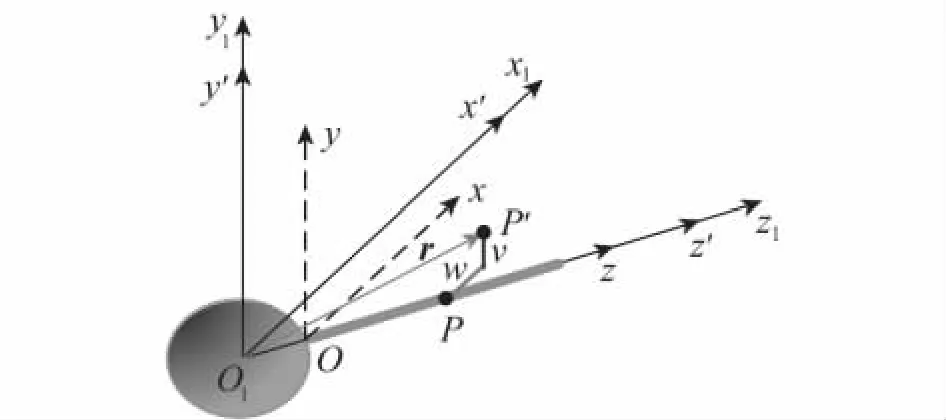
图1 旋转柔性叶片刚－柔耦合动力学模型Fig.1 Dynamic model of disc and blade rigid-flexible coupling system

2 动力学方程的建立

本文采用Hamilton原理建立旋转叶片系统的动力学方程，Hamilton原理的基本形式如下:

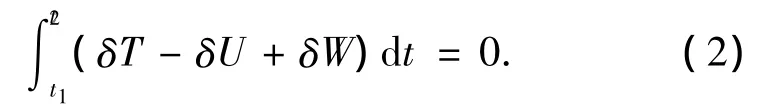
式中:T为系统的动能，U为系统的势能，δW为外力所作的虚功.考虑P点在动参考系Oxyz内的位移w(z)和v(z)是由两部分组成，即w=wb+ws，v= vb+vs，下脚标b表示由于弯曲引起的横向位移，下脚标s表示由于剪切引起的横向位移.旋转叶片系统动能由两部分组成，刚性圆盘的动能和柔性叶片的动能.在计算柔性叶片动能时，除考虑叶片微元随质心平动动能外，还计及叶片微元绕其截面形心惯性主轴转动动能，则系统动能可写为

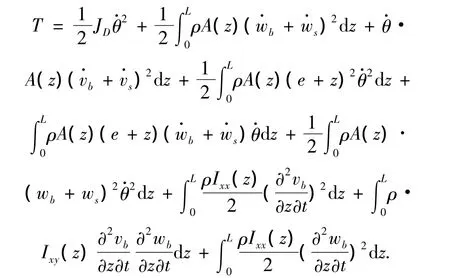
由弹性力学基本理论可知由弯曲产生的应变能Ub及剪切应变能Us分别为

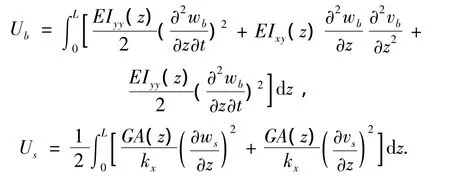
考虑叶片变形后微元体的向径为

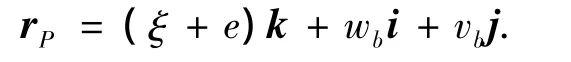
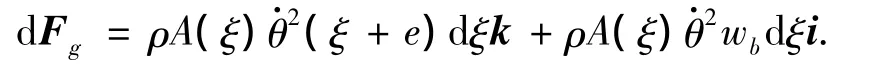
则作用于z截面处轴向离心惯性力可写为

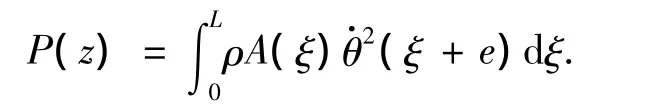
作用于dz微元体上单位长度的离心惯性力x轴方向上的分量可写为

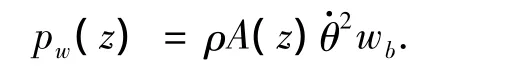
则由于xz平面内的弯曲而产生的离心力势能为

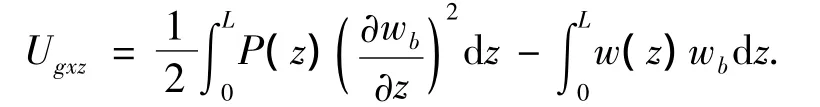
由于yz平面内的弯曲而产生的离心力势能为

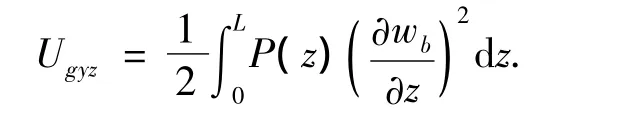
则旋转叶片系统势能为

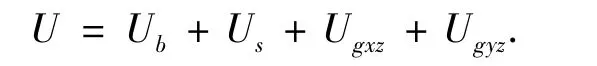
分别计算动能T、势能U和外力的功W对变形广义坐标w、v和刚性圆盘转动广义坐标θ的变分，并代入式(2)中，得系统的动力学方程为

3 系统离散动力学方程

采用有限元法给出系统离散动力学方程，将叶片视为旋转柔性梁，分成n个单元，第i个单元的长度设为li，如图2所示，设单元的节点位移为

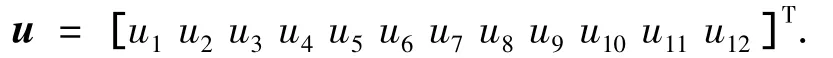
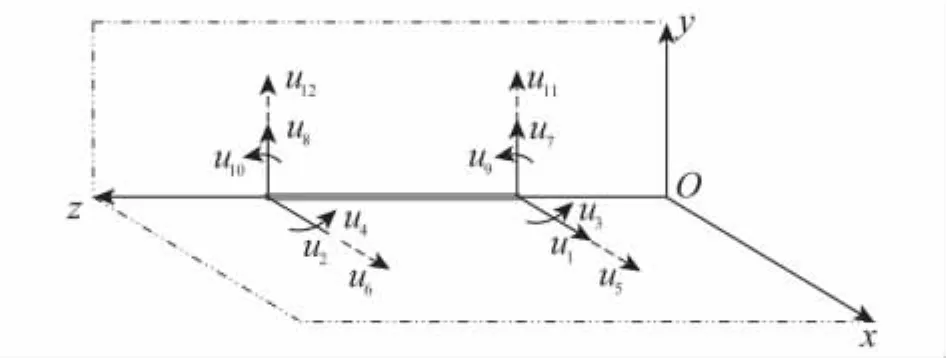
图2 旋转叶片单元节点位移Fig.2 Node displacements of a rotating flexible blade element

u1、u2、u3、u4为xz平面内弯曲引起的节点横向位移及转角位移，u5、u6为xz平面内剪切引起的节点横向位移.u7、u8、u9、u10为yz平面内弯曲引起的节点横向位移及转角位移，u11、u12为yz平面内剪切引起的节点横向位移，令

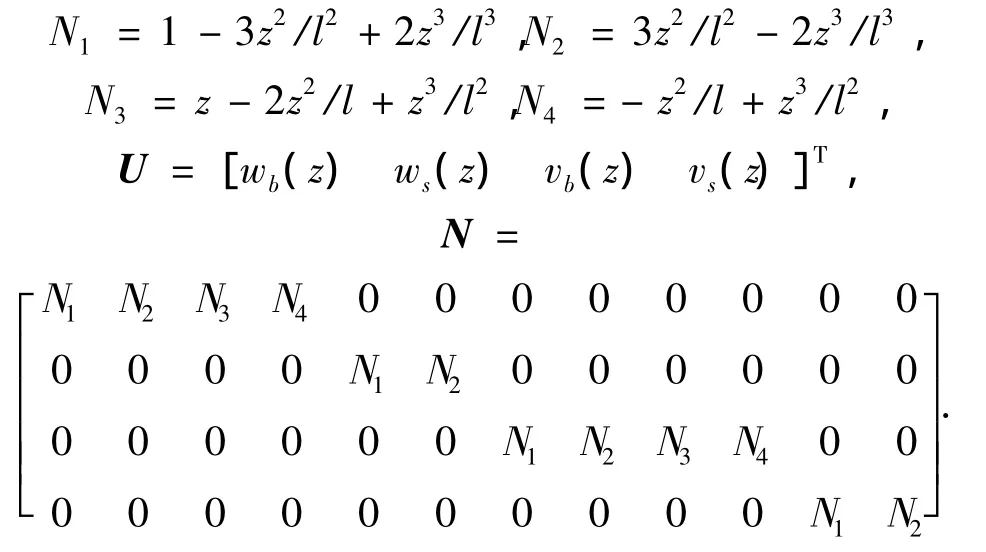
式中:U=Nu.

考虑双侧楔形带预扭角变截面旋转柔性叶片，叶片宽度、厚度和预扭角度沿叶片长度方向(轴方向)线性变化.如图3所示，叶片根部和端部截面宽度分别为b1、b2，厚度分别为h1、h2，预扭角度分别为θ1、θ2，注意到由于单元截面及扭转角沿z轴方向线性变化，故截面面积A及截面惯性矩Ixx、Ixy、Iyy是关于z的函数.将叶片单元离散，设单元局部坐标为，如图4所示，则第i个单元中性轴上P点未变形时在Oxyz坐标系内的位置可表示为

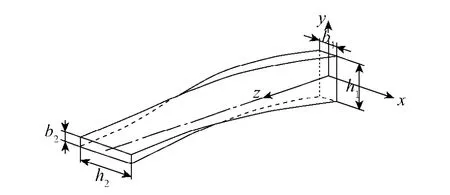
图3 带有预扭角变截面旋转叶片模型Fig.3 Sketch of a rotating blade with pre-twisted angle and variable cross-section

图4 旋转柔性叶片第i个单元局部坐标Fig.4 Local coordinate system of a rotating flexible blade element

令A=［1 0 0 0］，B=［0 1 0 0］，C=［0 0 1 0］，D=［0 0 0 1］.

叶片单元动能为

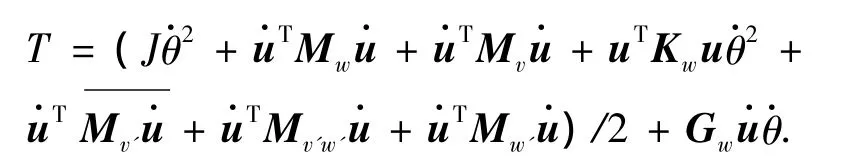
式中:

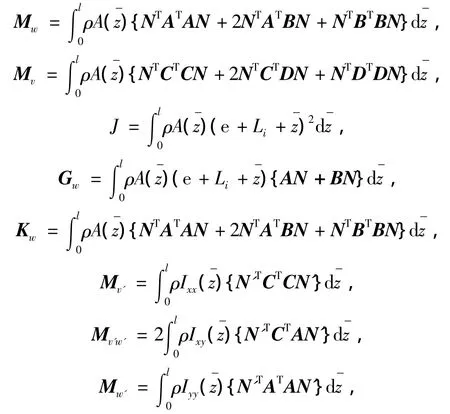
叶片单元势能为

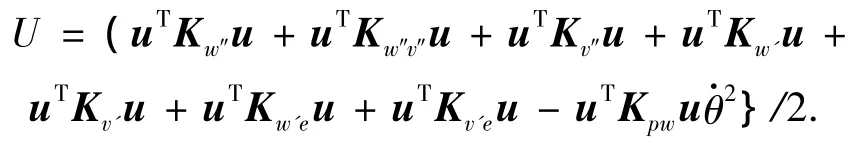
式中:

外力的虚功为

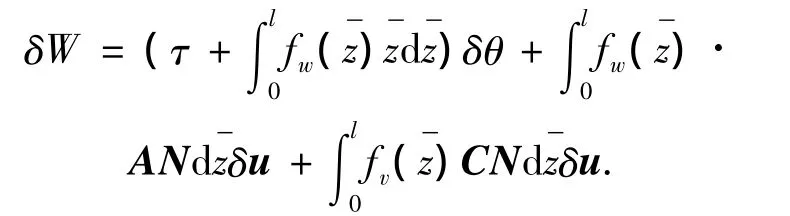
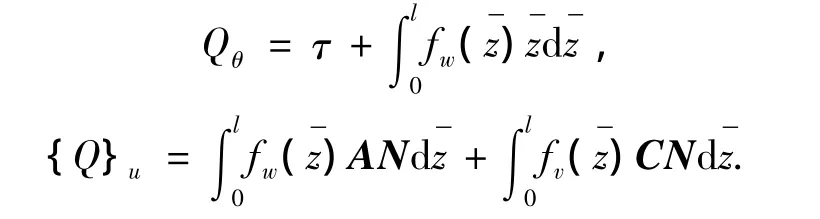
第i个单元的Lagrange函数为ψi=T－U并代入Lagrange方程得叶片第i个单元的动力学方程为

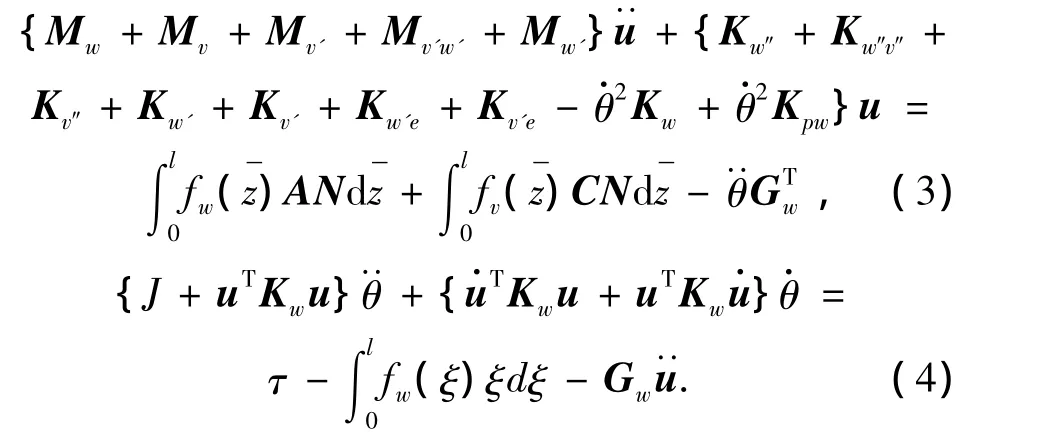
4 离散动力学方程的数值仿真

4.1 考虑预扭角变化叶片端部位移响应

叶片的参数取为L=0.6 m，b1=0.004 m，b2= 0.004 m，h1=0.15 m，h2=0.15 m，θ1=0°，ρ= 7 800 kg/m3，e=0.01 m，μ=0.3，E=2.07× 1011N/m2.

旋转角运动的规律取为

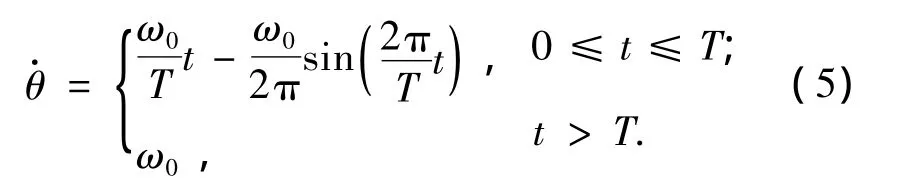
取n=500 r/min，T=150 s.

1)分别取θ2=0°、15°、30°、45°时，叶片端部位移的响应见图5.

由图5(a)和(c)可知，预扭角的变化对于xz平面内横向位移和转角位移没有影响.由图5(b)和(d)可知当无预扭时，yz平面内不产生横向位移和转角位移，当有预扭角时，尽管叶片只在xz平面内转动，也会在yz平面内产生横向位移及转角位移，且在15°～45°范围内随着预扭角增大，yz平面内横向位移及转角位移也随之增大.

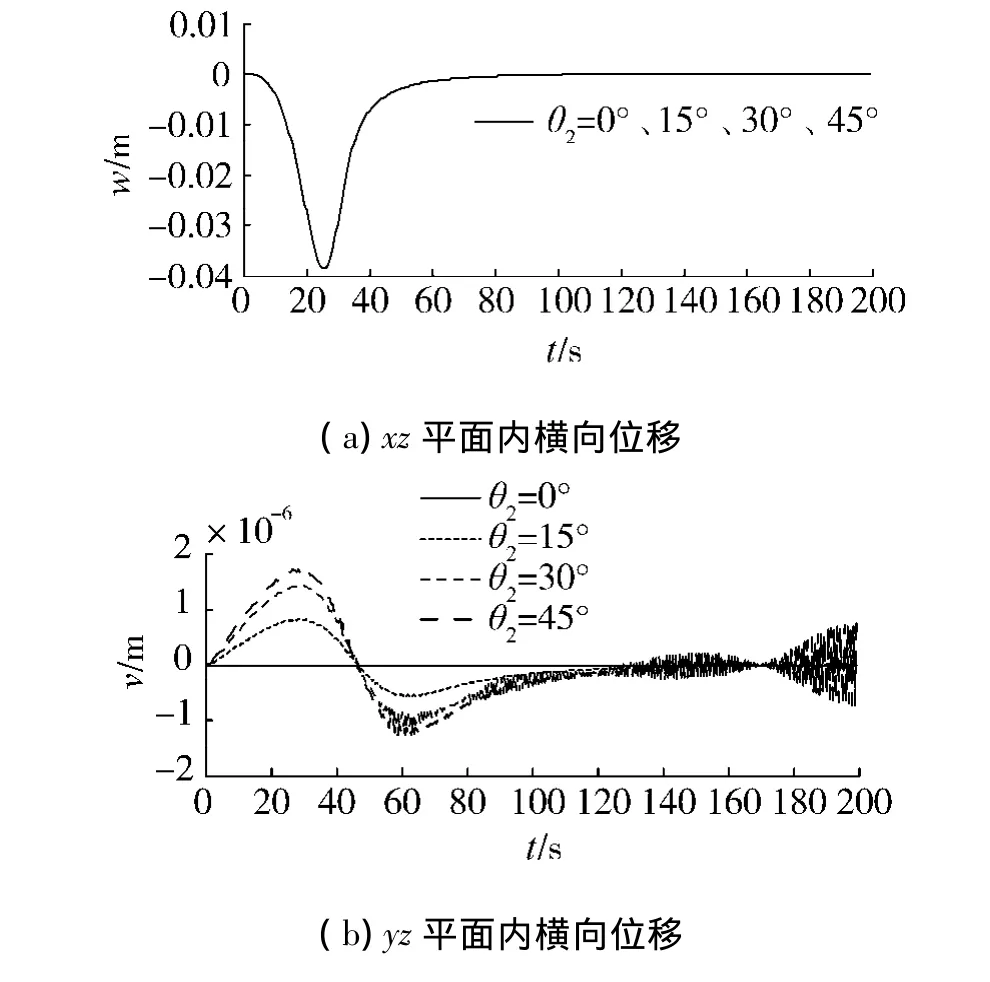
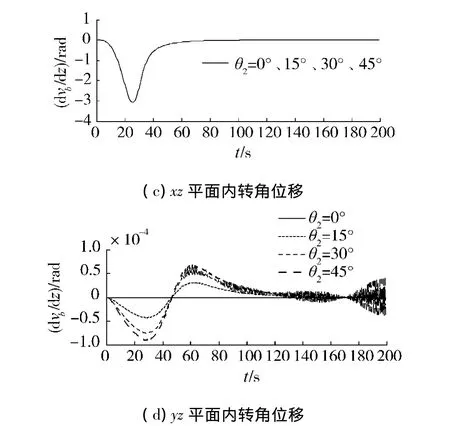
图5 叶片端部横向位移及转角位移Fig.5 Flexual and slope displacement of blade tip

2)分别取θ2=45°、60°、75°、90°时，叶片端部位移的响应见图6.

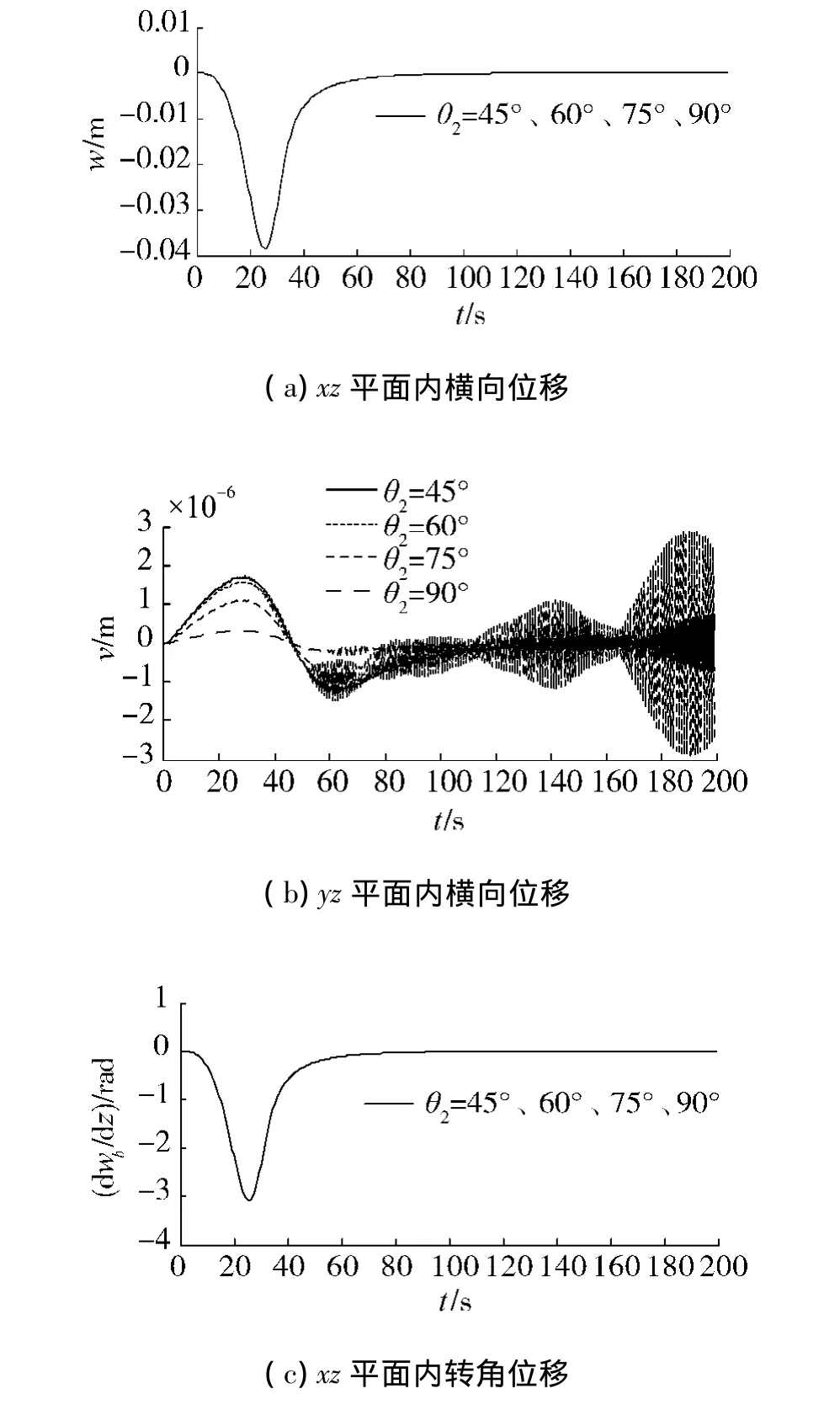
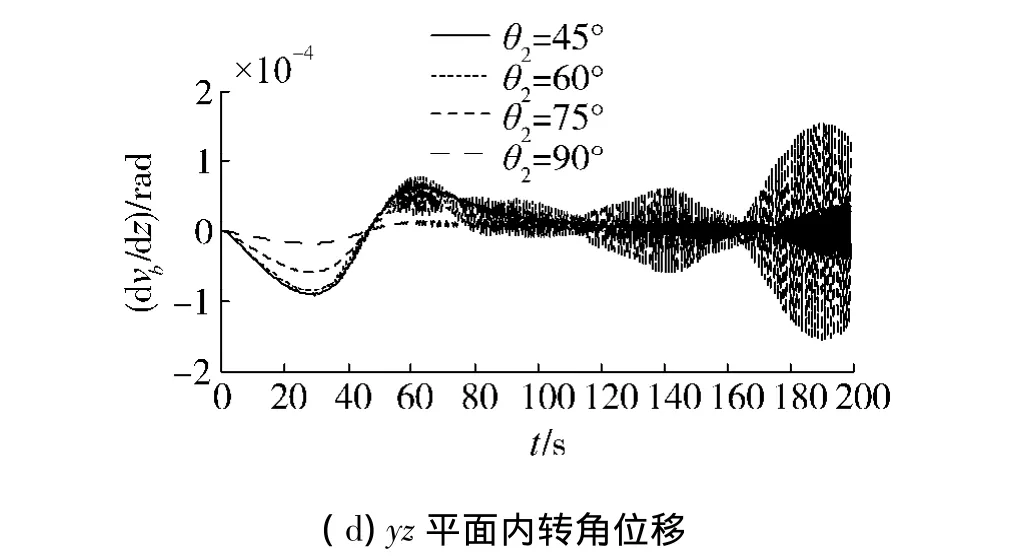
图6 叶片端部横向位移及转角位移Fig.6 Flexual and slope displacement of blade tip

由图6(a)和(c)可知，预扭角的变化对于xz平面内的横向位移和转角位移没有影响.由图6(b)和(d)可知，在45°～90°范围内随着预扭角的增大，yz平面内的横向位移及转角位移随之减小.仿真结果表明，位移响应是稳定的并不随时间发散.可见，预扭角的变化对yz平面内的横向位移及转角位移有较大影响.由于yz平面内的横向振动会使叶片系统动静部分发生碰擦，导致叶片通道堵塞，产生严重的摩擦声，引发叶片断裂事故.

4.2 考虑截面变化叶片端部位移响应

叶片的参数取为L=0.6 m，b1=0.004 m，h1= 0.15 m，θ1=0°，θ2=45°.旋转角运动的规律取式(5)，取n=500 r/min，T=150 s.

考虑截面变化时叶片端部位移响应，见图7.

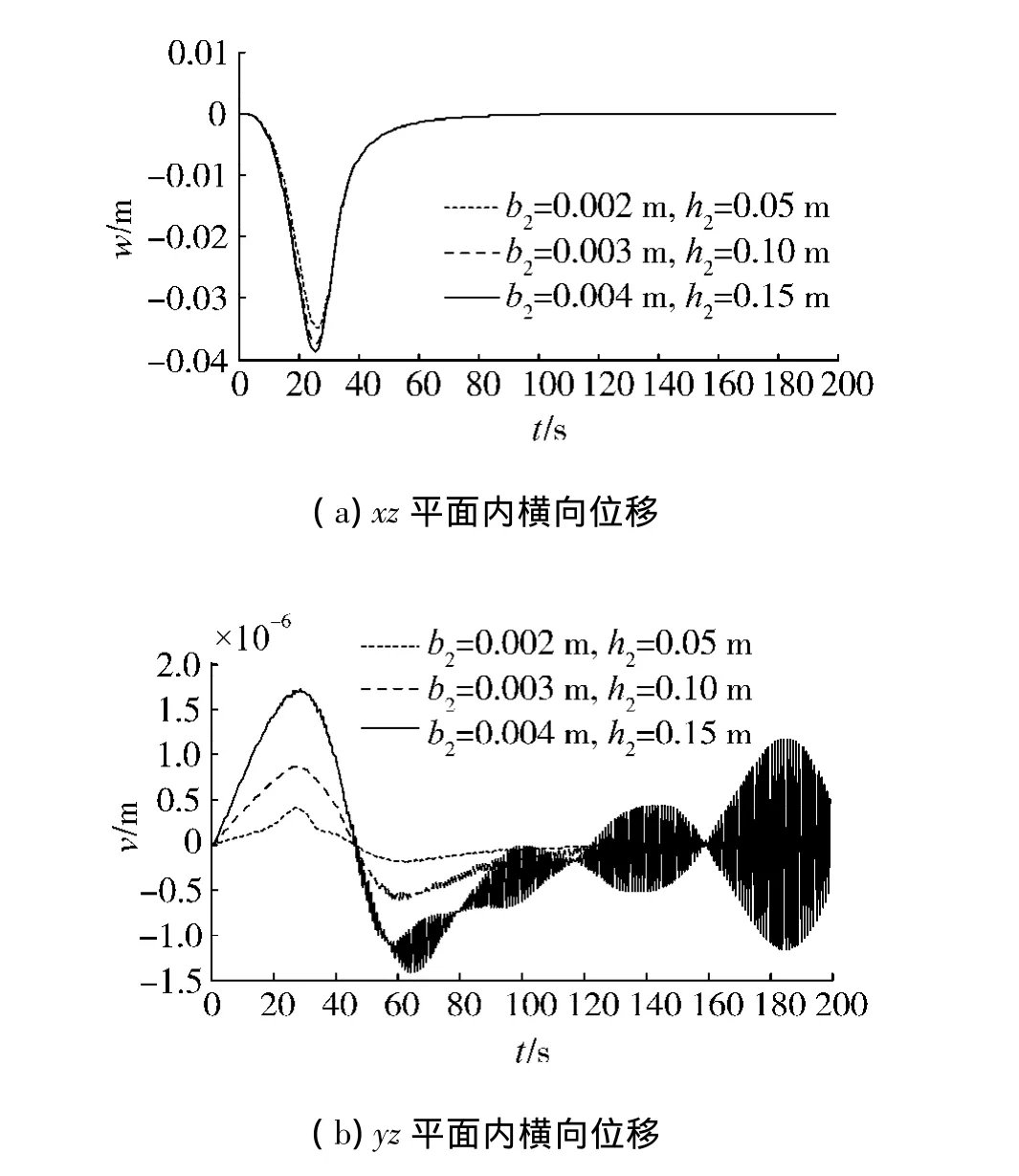
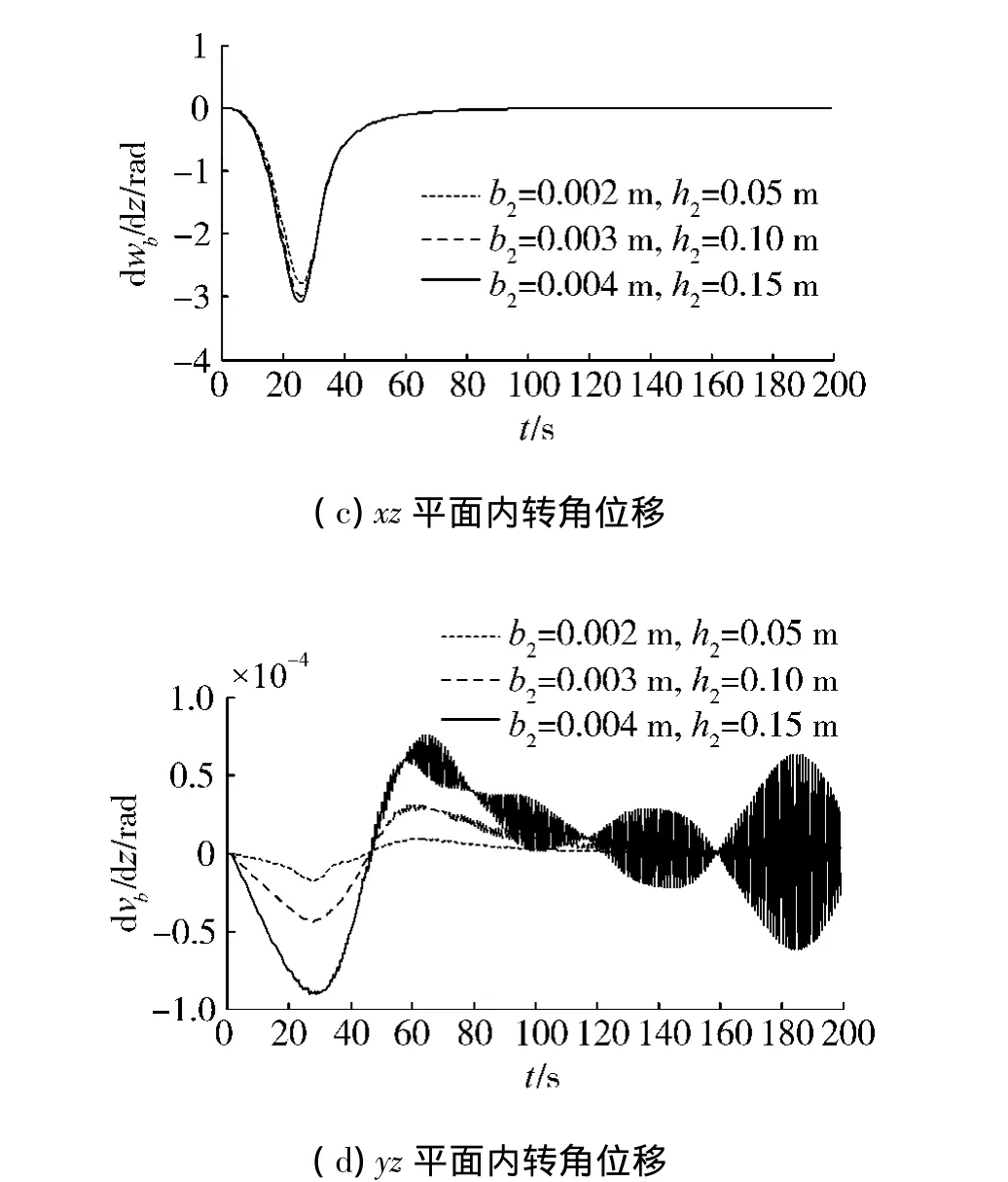
图7 叶片端部横向位移及转角位移Fig.7 Flexual and slope displacement of blade tip

由图7(a)～(d)可以看出，叶片截面宽度和高度的变化对xz平面内的横向位移和转角位移影响较小，而对于yz平面内的横向位移和转角位移有较大影响.

5 结束语

基于Hamilton变分原理推导了带有预扭角、变截面，考虑剪切变形、截面转角及离心刚化效应的大范围旋转柔性叶片刚柔耦合系统非线性偏微分积分连续动力学方程组.基于有限元法建立了旋转叶片系统非线性、时变及完全耦合的有限维离散动力学方程，基于数值仿真结果分析了截面参数对叶片横向位移的影响，为变截面叶片的设计提供了理论依据，同时也为后续叶片位移响应的稳定性分析及幅频特性研究提供了理论基础及分析数据.

［1］ERIGEN A C.On the non-linear vibration of elastic bars［J］.Q Appled Mathematics，1952，9:361-369.

［2］WOODALL S R.On the large amplitude oscillations of a thin elastic beam［J］.Journal of Non-Linear Mechanics，1966，1:217-238.

［3］ANDERSON G L.On the extensional and flexual vibrations of rotating bars［J］.Journal of Non-Linear Mechanics，1975，10:223-236.

［4］HODGES D H.On the extensional vibrations of rotating bars［J］.Journal of Non-Linear Mechanics，1977，12:293-296.

［5］ANSARI K A.Non-linear vibrations of a rotating pretwisted blade［J］.Computers＆Structures，1975，5:101-108.

［6］LIM Hongseok.Impact analysis of a rotating beam due to particle mass collision［J］.Journal of Sound and vibration，2007，308:794-804.

［7］YOO Honghee.Model analysis and shape optimization of rotating cantilever beams［J］.Journal of Sound and vibration，2006，290:223-241.

［8］YANG Chiahao.The influence of discs flexibility on coupling vibration of shaft-dics-blades system［J］.Journal of Sound and Vibration，2007，301:1-17.

［9］PARK Junghun，PARK Hyunijong，JEONG Seokyong，et al.Linear vibration analysis of rotating wind-turbine blade［J］.Current Applied Physics，2010，10(2):S332-S334.