梢涡空化CFD数值方法

韩宝玉，熊鹰，刘志华

(海军工程大学 船舶与动力学院，湖北 武汉 430033)

梢涡空化是螺旋桨及高速艇水翼空化的主要组成部分.梢涡空化发生时，不仅会辐射大量噪声，诱发船体振动，还会使桨后舵产生严重剥蚀.在设计中要控制甚或消除梢涡空化的这些不利影响，需要准确了解梢涡流场的物理特征及空化的形成机理.

实验研究［1-4］在揭示螺旋桨及水翼梢涡空化的形成和发展方面做了大量工作.与实验相比，数值方法成本低且能得到流场内部多数细节问题，有助于人们理解内部流场的特征，因此应用数值方法模拟升力体梢涡空化非常有意义.

当前，应用RANS方法结合多相流理论模拟空化流形态及其分布，以此预报空化对流体机械性能的影响是数值研究的热点.RANS方法在计算梢涡流场时的难点是数值离散精度，涡核处网格尺度及湍流模型;而多相流理论中难点在于如何建立空化模型.

Dacles-Mariani等［5］研究了RANS方法中数值离散和网格尺度对梢涡计算精度的影响，认为对方程非粘性项离散要达到五阶精度，涡核横剖面每个方向至少有15个网格节点才能准确计算涡的流场分布.Spall等［6］通过对网格的特殊处理，认为在梢涡流场计算中只要涡核处网格尺度合适，二阶离散的精度就可以达到工程要求.在湍流模型研究方面，Churchfield等［7］发现现有的未经过旋转和曲率修正的一方程和两方程湍流模型都过高预报了涡核处的湍流粘性耗散，导致涡强迅速减小.而经过旋转和曲率修正［8］的湍流模型有效抑制了涡核处的粘性耗散，提高了计算精度.

空化模型方面，黄胜等［9］应用完全空化模型模拟了二维翼稳态空泡.韩宝玉等［10］用改进 VOF (volume fraction)模型［11］模拟了NACA66二维翼型的非稳态空化分布，对低空泡数时非稳态空泡的发展、脱落现象进行了研究.

本文以翼剖面为NACA16020翼型的椭圆形水翼为研究对象，采用经过旋转和曲率修正的代数雷诺应力湍流模型预报了水翼梢涡流场分布，并与实验结果进行了对比.在此基础上，用改进VOF模型模拟了不同空泡数下梢涡空化的轨迹和形态，并对梢涡空泡消失空泡数进行了预报.

1 数学方法

1.1 数值方法及湍流模型

控制方程为

梢涡流场中的高曲率及强旋转流动导致湍动粘度的各向异性影响较大，应用涡粘性湍流模型模拟的流场分布与实验结果明显不符.为了克服这些缺点，Wallin等［12］提出了显式代数雷诺应力模型(EARSM)，该模型对雷诺应力的输运方程进行了简化处理，忽略了方程中一些关乎次要流动现象的高阶项，建立了雷诺应力与应变率张量和涡张量间的非线性关系式，考虑了湍流各向异性的影响.实验表明梢涡流场的高旋度及流线的高曲率造成的近似刚体旋转运动稳定了梢涡内流场分布，使梢涡尾流中的湍动能迅速衰减.为了捕捉涡的这种稳定效应，Wallin等［13］提出了适用于EARSM湍流模型的旋转和曲率修正方法，以减小涡核内的湍动粘性耗散.韩宝玉等［14］通过对常用两方程模型和代EARSM模型进行旋转和曲率修正，研究了湍流模型对机翼梢涡流场数值模拟的影响.发现经过修正的EARSM湍流模型计算结果较其他湍流模型与试验结果吻合更好.以此为依据，本文计算中选用经过旋转和曲率修正的EARSM湍流模型.

1.2 空化模型

根据Bakir等［11］提出的理论，混合相由液相、汽相和不可压离散气体3部分组成.假定混合相速度相同，混合相密度:

把气体和液相看作一体(用下标m表示)，假定气体的质量分数为常数，其密度ρm可表示为

式中:ρ为密度，y为质量分数，下标d表示离散气体，l表示水，v表示汽相，y*=ρ*/α*/ρ.该混合相的连续方程为

式中:α为体积分数，汽相体积分数αv=1－αm;=－，为混合相和汽相之间质量交换率.显然只需知道的表达式，联立式(1)～(5)即可求得汽相体积分数.

分析球形气泡脉动过程可得

式中:Rb为气泡半径，N为单位体积内气泡的数目.根据Rayleigh-Plesset方程，忽略方程二阶项及粘性项，可得

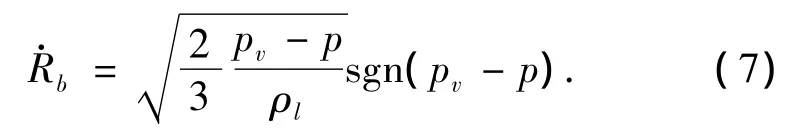
式中:pv、p、ρl分别为气化压力、流场压力、水的密度.而

根据式(6)～(8)可得

式中:Fc是经验系数，用于修正气泡膨胀和收缩的速度.在式(4)～(9)中，yd、Rb、Fc均为经验常数.根据文献［10］，当pv－p＞0时，Fc=100;当pv－p≤0时，Fc=0.005.计算中认为yd=1.3×10－7，Rb=1×10－6m.

2 计算模型及网格划分

本文的计算模型是翼剖面为NACA16020翼形的半椭圆形水翼，翼最大弦长C=0.475 m，展长L=0.712 5 m.实验［1］在空泡水洞中完成，工作段的横剖面尺寸为1.14 m×1.14 m.来流速度 V= 10 m/s，基于弦长和来流速度的雷诺数为4.75× 106，翼攻角α=10°.

为了验证计算方法的准确度，本文建立的计算域与实验一致.原点在翼根弦长中心处，入口和出口与翼导边和随边距离分别为2.5 C，10.0 C.计算域及坐标系如图1所示.

图1 计算域Fig.1 Domain used in computations

根据计算域的几何形状，本文主要用H型网格对计算域进行整体网格划分，见图2.考虑到梢涡的形成与翼边界层内流动有关，为了较准确地模拟边界层内流场，本文应用O型网格对翼壁面附近的网格进行了处理，以提高网格质量，第一层网格尺度y+在1～30之间.

图2 计算域网格示意Fig.2 Overall view of computational domain grid

由于梢涡涡核内径向速度梯度较大，为了减小该区域的数值离散误差，本文对梢涡涡核区域的网格进行加密，使涡核内径向网格节点数达到50×50以上，整个计算域网格总数为500万.

在边界条件设置上，来流为了保证速度和雷诺数与实验一致，设置进口的总压为151 170 Pa，对应来流速度为10 m/s，入口处的湍流强度为0.15%，涡粘比为5;出口边界条件为质量流率12 957 kg/s;翼表面及计算域上下表面为不可滑移物面边界条件.计算在商用CFD软件CFX中完成.

3 计算结果与分析

本文首先计算了水翼梢涡流场速度分布，通过与实验对比验证该方法的可行性.在此基础上应用相变空化模型对梢涡空化特性进行了研究.

3.1 尾流中梢涡流场特性

尾流中梢涡的近似刚体旋转运动给梢涡流场的数值预报增加了难度，在模拟梢涡内流场特性时，应用标准代数雷诺应力模型(EARSM)模型和经旋转和曲率修正后的湍流模型(EARSM-CC)计算结果有明显差别.

图3和图4分别对比了x方向3个位置处梢涡内无因次轴向速度(U/U∞)和切向速度(Vt/U∞)沿z轴分布的计算结果和实验结果.

图3 梢涡内轴向速度分布Fig.3 Profiles of velocity in tip vortex

从图3中可以看出，在各个x位置处，未经修正的代数雷诺应力模型预报的轴向速度峰值明显低于实验结果，尤其在x/C=0.3时其峰值低于来流速度，与实验结果截然相反.这是因为随梢涡向下游发展，梢涡的近似刚体旋转加强，使得涡粘性耗散减小，而未经修正的湍流模型过高地预报了梢涡内湍流粘性耗散，导致梢涡内速度递减过快.而经过旋转和曲率修正的代数雷诺应力模型则有效减缓了这种湍动粘性耗散，尤其在近场x/C=0.1处与实验结果吻合很好.而该位置处正是梢涡空化初生的关键位置，为后续空化初生的研究提供了保证.

从图4可以看出，经过旋转和曲率修正的湍流模型准确预报出了各个x位置处的切向速度分布，与实验结果吻合较好;而未经修正的湍流模型则过低地预报了切向速度的峰值，与实验结果差距明显.从实验结果可以看出，在尾流近场各个x位置处，当z＜0时，梢涡内流场切向速度存在明显的波动，且曲线呈现严重的不对称性.文献［15］认为造成这种波动的原因是水翼后二次涡对梢涡的干扰，计算准确模拟出了二次涡的这种干扰作用.

图4 梢涡内切向速度分布Fig.4 Profiles of tangential velocity in tip vortex

图5为应用修正后的湍流模型计算的梢涡涡强无因次轴向分量(ωx×C/U∞)在x/C=0.1和0.2处云图(视角为从下游往上游看)，图中可见梢涡主涡和二次涡.从图中可以看出，在x/C=0.1处二次涡的强度比较大，对主涡的影响较明显，这从图4计算结果中可以看到.随着梢涡往下游发展，二次涡与壁面发生分离，并逐渐融合到主涡中去.这种现象可以从图6中看到，图中主涡所指曲面为ωx×C/U∞=100等值面，二次涡所指曲面为 ωx× C/U∞=－20等值面.

图5 梢涡的形成和卷曲Fig.5 Formation and rollup of the tip vortex

图6 无因次轴向涡强等值面图Fig.6 Iso-surfaces of normalized axial vorticity

3.2 梢涡空泡数值模拟

前文计算结果显示，在计算水翼梢涡近场速度分布时，本文所用的湍流模型及网格尺度是可信的.在此基础上，本文引入改进VOF模型，对水翼梢涡空泡消失的临界空泡数及梢涡空泡形态进行了预报研究.

梢涡空化的初生是流体中气核膨胀直至形成肉眼可见的空泡的过程，由于气核的膨胀需要一定时间，而相变模型基于空化在瞬间形成和溃灭的假定，因此该模型在预报梢涡空化从无到有的初生过程存在先天缺陷.在实验测量中空泡的初生空泡数受实验条件的影响较大，而消失空泡数则比较稳定，因此人们通常用消失空泡数作为空泡发生的衡准数.和空泡初生相比，空泡的溃灭是短暂的，因此应用相变模型预报梢涡空泡的消失空泡数具有一定的可行性.

图7为水翼在空泡数σ=2.5、2.6、2.7、2.8时汽相体积分数αv=0.1的等值面计算结果.从图中可以看出，在该空泡数范围内，水翼只出现梢涡空化，而片状空泡尚未出现.随空泡数增大梢涡空泡的横截面尺寸减小，空泡条纹越来越短.文献［16］认为当空泡尺寸达到1～3 mm时认为空化消失，本文以2 mm为判断依据.当空泡数达到2.6～2.7时，该等值面横截面尺寸达到2 mm左右，此时可定义为空泡消失，其空泡数即为空化消失空泡数σd，计算值与实验［1］测量结果σd=2.65吻合较好.

图7 不同空泡数时梢涡水汽含量等值面图(αv=0.1)Fig.7 Iso-surfaces of water vapour volume fraction αv=0.1 in different cavitation number

4 结论

本文应用RANS方法计算了翼剖面为NACA16020翼型的椭圆形水翼梢涡流场分布，并结合改进VOF相变空化模型对梢涡空泡特性进行了研究，得出以下结论:

1)在计算近似刚性体旋转运动的梢涡流场时，未经旋转和曲率修正的湍流模型过高地预报了尾流场中的粘性耗散，导致涡核内轴向速度减小过快.而经过修正的代数雷诺应力湍流模型较好地改进了计算结果，与实验吻合较好.

2)本文应用的数值方法准确预报出了梢涡内主涡和二次涡的关系，与实验测量结果相符，为后续对梢涡空泡的研究奠定基础.

3)应用相变空化模型预报梢涡空泡的轨迹和消失空泡数是可行的，其预报结果与实验吻合较好.

［1］FRUMAN D H，DUGUE C，CERRUTTI P.Tip vortex rollup and cavitation［C］//19th Symposium on Naval Hydrodynamic.Washington D C，USA，1992:633-654.

［2］ARNDT R E A，ARAKERI V H，HIGUCHI H.Some observations of tip-vortex cavitation［J］.Journal of Fluid Mechanics，1991，229:269-289.

［3］ARNDT R E A，MAINES B H.Viscous effects in tip vortex cavitation and nucleation［C］//20th Symposium on Naval Hydrodynamic.Washington D C，USA，1994:268-289.

［4］MAINES B H，ARNDT R E A.Tip vortex formation and cavitation［J］.Journal of Fluid Engineering，1997，119: 413-419.

［5］DACLES-MARIANI J，KWAK D，ZILLIAC G.On numerical errors and turbulence modeling in tip vortex flow prediction［J］.International Journal for Numerical Methods in Fluids，1999，30:65-82.

［6］SPALL R E.Numerical study of a wing-tip vortex using the Euler equations［J］.Journal of Aircraft，2001，38(1):22-27.

［7］CHURCHFIELD M J，BLAISDELL G A.Near field wingtip vortex computation using the WIND code［R］.Washington DC:AIAA，2006.

［8］SPALART P R，SHUR M.On the sensitization of turbulence models to rotation and curvature［J］.Aerospace Science and Technology，1997，5:297-302.

［9］HUANG Sheng，HE Miao，WANG Chao，et al.Simulation of cavitating flow around a 2-D hydrofoil［J］.Journal of Marine Science and Application，2010，1:63-68.

［10］韩宝玉，熊鹰，陈双桥.对二维翼空化流动的数值模拟［J］.水动力学研究与进展，2009，24(6):740-746.

HAN Baoyu，XIONG Ying，CHEN Shuangqiao.Numerical simulation of cavitation around 2-dimentional hydrofoil［J］.Chinese Journal of Hydrodynamics，2009，24(6):740-746.

［11］BAKIR F，REY R，GERBER A G.Numerical and experimental investigations of the cavitating behavior of an inducer［J］.International Journal of Rotating Machinery，2004，10:15-25.

［12］WALLIN S，IOHANSSON A.A complete explicit algebraic Reynolds stress model for incompressible and compressible flows［J］.Journal of Fluid Mechanics，2000，403:89-132.

［13］WALLIN S，IOHANSSON A.Modeling streamline curvature effects in explicit algebraic Reynolds stress turbulence models［J］.International Journal of Heat and Fluid Flow，2002，23(5):721-730.

［14］韩宝玉，熊鹰，叶金铭.湍流模型对三维翼梢涡流场数值模拟的影响［J］.航空学报，2010，31(12):2342-2347.

HAN Baoyu，XIONG Ying，YE Jinming.Effect of turbulence models on numerical simulation of tip vortex flow field behind 3D wing［J］.Acta Aeronautica et Astronautica Sinica，2010，31(12):2342-2347.

［15］ARNDT R E A，KELLER A P.Water quality effects on cavitation inception in a trailing vortex［J］.Journal of Fluids Engineering，1992，114:430-438.

［16］盛振邦，刘应中.船舶原理(下)［M］.上海:上海交通大学出版社，2004:68.