多频带自适应脉冲设计

郭黎利，赵冰

(哈尔滨工程大学 信息与通信工程学院，黑龙江 哈尔滨 150001)

随着无线通信技术飞速发展，频谱资源日趋紧张，认知无线电(cognitive radio，CR)和超宽带无线通信(ultra wide band，UWB)作为解决频谱紧张的两大技术成为无线通信领域新的研究热点.认知无线电技术是一种智能的频谱共享技术，它能够主动感知频谱环境，通过一定的方法寻找未使用的频带，调整通信终端的参数设置，实现空闲的频谱资源的介入，从而达到提高频谱利用率、缓解频谱资源紧张的目的［1］.超宽带无线通信技术基于共用频带的思想，与现有传统窄带无线技术共享频带，但是由于其所占的频谱范围很宽，且在设计过程中与外界环境没有交互，频谱共享缺乏灵活性，限制了频谱利用率的提高.将认知无线电技术与超宽带无线通信技术相结合［2-3］，设计出一种新的智能无线系统——认知超宽带无线通信系统(cognitive ultra wide band，CUWB).

在UWB系统中，脉冲形成器中脉冲波形的选择是至关重要的，此外脉冲的功率谱密度必须满足美国联邦通讯委员会(FCC)辐射掩蔽的限制，脉冲的特性制约了整个系统的性能、复杂度和频谱利用情况.常用的UWB脉冲主要有高斯脉冲及其导数组合、Rayleigh脉冲、Morlet小波脉冲以及厄密特脉冲等.高斯脉冲及其导数的组合脉冲能够很好的满足辐射掩蔽要求，频谱利用率较高，但是计算量较大，加权系数精度难以掌握［4］;Rayleigh脉冲本质上与高斯脉冲类似，不易于窄带系统共存;Morlet小波脉冲的时域特性和频域特性均不错，能够满足FCC的辐射限制，频谱利用率高，但表达式中有频移项，适用于基于频移脉冲方式的UWB系统［5］;厄密特各阶脉冲间互相正交，可以降低误码率和用户间干扰，但其能量集中于低频，各阶波形频谱相差大，需借助载波搬移频谱满足FCC要求［6］.

针对上述脉冲设计方法中存在的问题，本文提出一种结合认知无线电技术的无载波多频带自适应脉冲设计方法，该脉冲具有计算量小，参数易于控制，不需要载波搬移频谱，频谱利用率较高，可实时的修正波形等特点，与现有窄带通信系统有很好的兼容性.

1 CUWB自适应脉冲

1.1 扁长椭球波函数集

为了实现高速率传输和低符号间干扰，脉冲的的持续时间要尽量短，即脉冲为时限信号.同时脉冲的频谱要限定在频谱空洞内，不能对其他用户产生干扰，即脉冲为带限信号.由奈奎斯特定律可知:频域上集中的信号必定在时域上分散，反之亦然.因此如何找到这样一组脉冲是目前研究的热点.D.Slepian等发现在椭球坐标系下求解赫姆霍兹方程时获得的椭球波函数集可有效地解决这一问题［7］.

扁长椭球波函数(PSWF)是带限［－ω，ω］和时限［－T/2，T/2］空间上的完备正交基［8-9］:

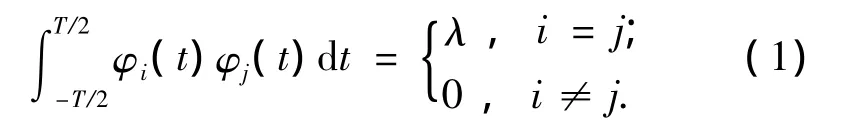
扁长椭球波函数满足下列积分方程:

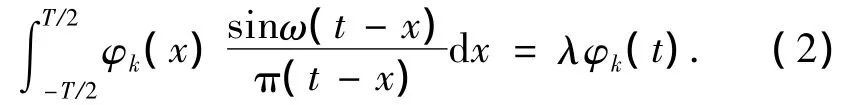
式中:φk(x)为第k阶扁长椭球波函数，λ为对应的特征值，1＞λ0＞λ1＞…＞λk＞…，

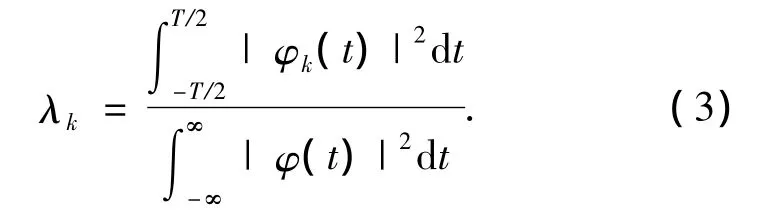
式中:λk表示第k阶PSWF的能量集中度.由式(3)可以看出，φ(x)经过截止频率ω的低通滤波器之后，输出的是经过特征值λ加权后的函数本身φ(x).

将上式进行变换得到

由式(4)可以看出，时限扁长椭球波函数φ(x)经过截止频率［ωl，ωh］的带通滤波器h(t)之后，输出仍是它本身.φ(x)的频谱具有相同的特性:

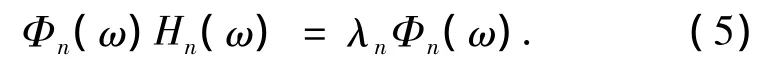
式中:Φn(ω)为φ(x)的频谱，Hn(ω)为h(t)的傅里叶变换.

1.2 自适应脉冲设计

认知无线电首先对接收到的射频信号进行干扰温度估计并检测频谱空洞，然后将可用频带按优先级排列、标识，并制定完备的退让和替代策略.当授权用户重新接入时，可选择跳转到备用频带或降低功率级数，以避免对授权用户产生干扰.

对选定的通信频带构建动态自适应辐射掩蔽SCUWB(f).根据自适应辐射掩蔽规定的功率谱形状和覆盖范围，利用PSWF设计脉冲波形.PSWF具有计算量小，各阶脉冲相互正交，生成简单及接入灵活等优点，但单频带PSWF的频谱利用率较低.因此，本文借鉴OFDM的思想，将频带划分成若干个子带，并根据子带信道特性生成相应的子带辐射掩蔽.根据各子带的约束条件，利用PSWF产生相应的子带波形，并在时域上将子带脉冲进行加权累加.在所有满足条件的波形中，选择具有最大能量集中度的φ0作为子带脉冲pi(t):

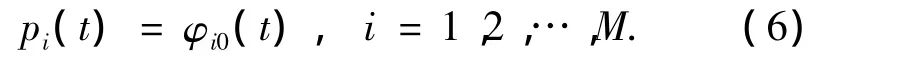
式中:M为子带个数.

自适应脉冲波形为

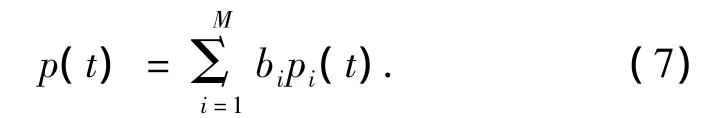
式中:bi为对应子带的加权系数.

根据傅里叶变换的线性性质，自适应脉冲的频谱等于子带脉冲频谱的线性叠加:

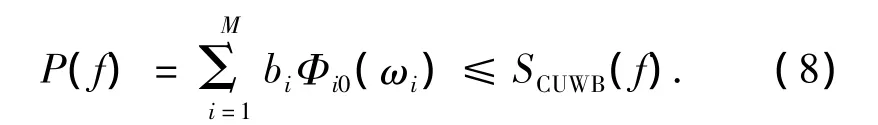
图1为多频带自适应脉冲的原理图，可用频带被划分成多个子带，根据子带自适应辐射掩蔽生成的子带脉冲在时域上被叠加.当系统检测到窄带干扰时，自适应辐射掩蔽发生变化，在干扰信号所在的频带内产生凹槽，该频带内的子带脉冲被撤销，利用剩余频带继续通信.在出现少量窄带干扰的情况下，系统不需要跳转到备用频带，从而实现无缝的修正发射波形以适应无线环境.

图2对上述多频带自适应脉冲进行了仿真.从图2(a)中可以看出脉冲的带外特性很好，衰减速率很快，频谱利用率也较高.从图2(b)可看出在窄带干扰处，脉冲可产生深度达到40dB以上的凹槽，这些凹槽可以使CUWB系统避免与这一频带上的窄带系统产生干扰，从而实现共存.

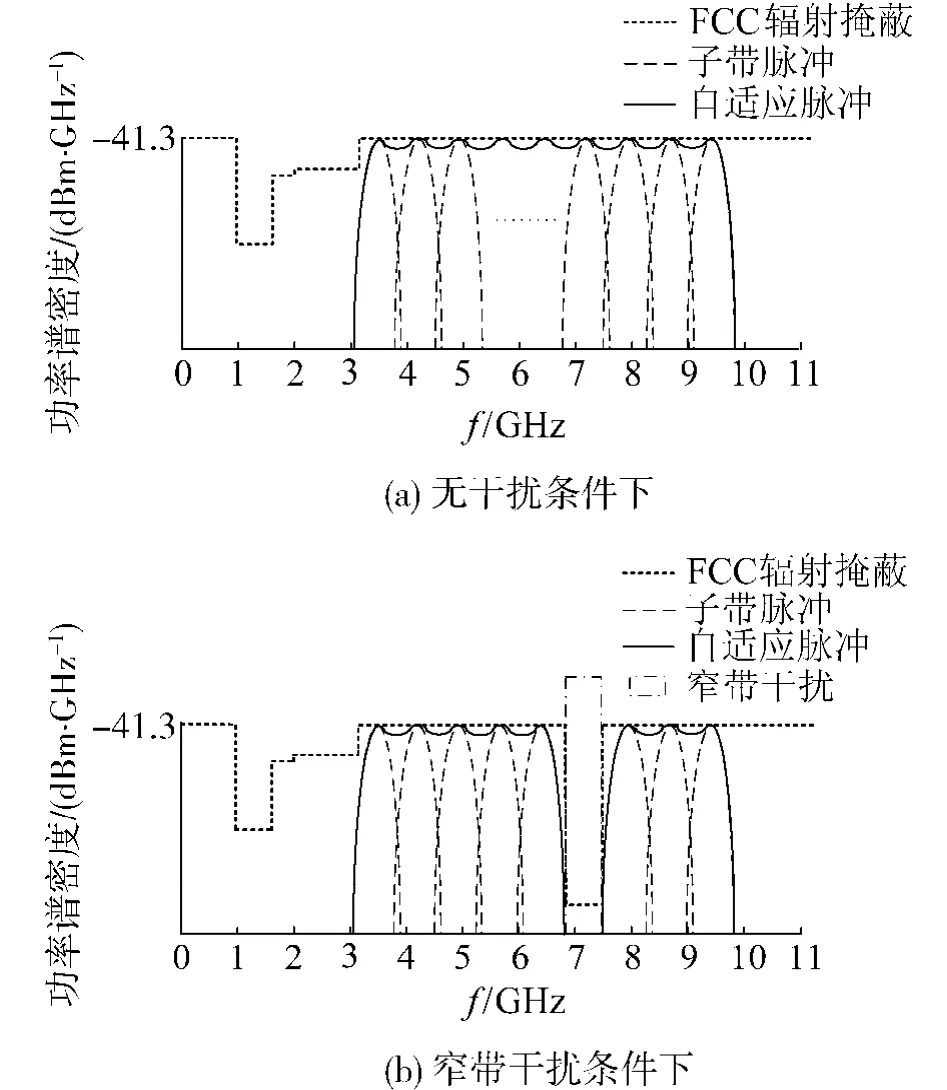
图1 多频带自适应脉冲Fig.1 Multi band adaptive pulse waveform

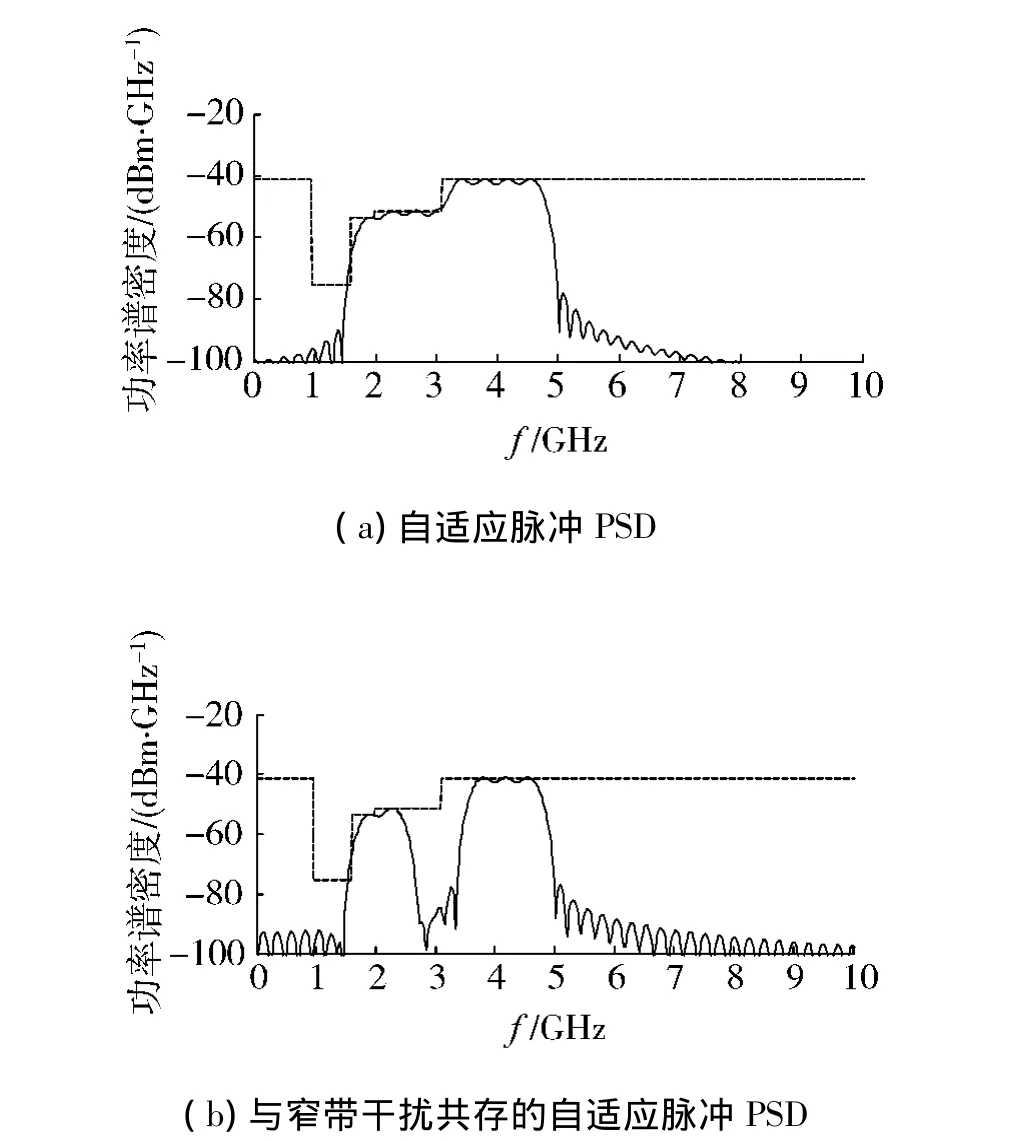
图2 自适应脉冲功率谱密度Fig.2 PSD of adaptive pulse waveform

2 脉冲频谱利用率

计算脉冲频谱利用率是衡量CUWB脉冲优劣的一种方式［10］，定义脉冲的带通为Bp，则频谱利用率为

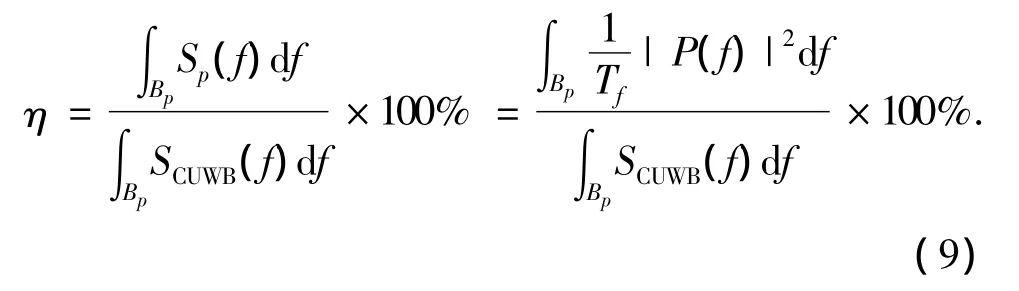
式中:Tf为脉冲重复周期.

为了更好地利用频谱资源，提高频谱利用率，在划分各子带时并不是完全独立的，子带间有部分频带是相互重叠的，定义频带重叠率ξ为

式中:Bi为子带频谱宽度，Bμ为重叠部分宽度.

自适应脉冲频谱宽度Bp为

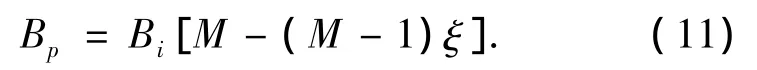
频谱利用率η主要受频带重叠率ζ和子带宽度βi的影响.在子带宽度确定的情况下，ζ的增大会引起子带个数M的增加，导致计算量加大，系统复杂度增高.图3为在子带宽度不变的情况下，频谱利用率与频带重叠率之间的关系.从图3可以看出，随着频带重叠率的增加，脉冲的频谱利用率也逐渐增大.当频带重叠率达到最大时，频谱利用率达到85%以上.当存在窄带干扰时，自适应脉冲仍可以保持较高的频谱利用率.

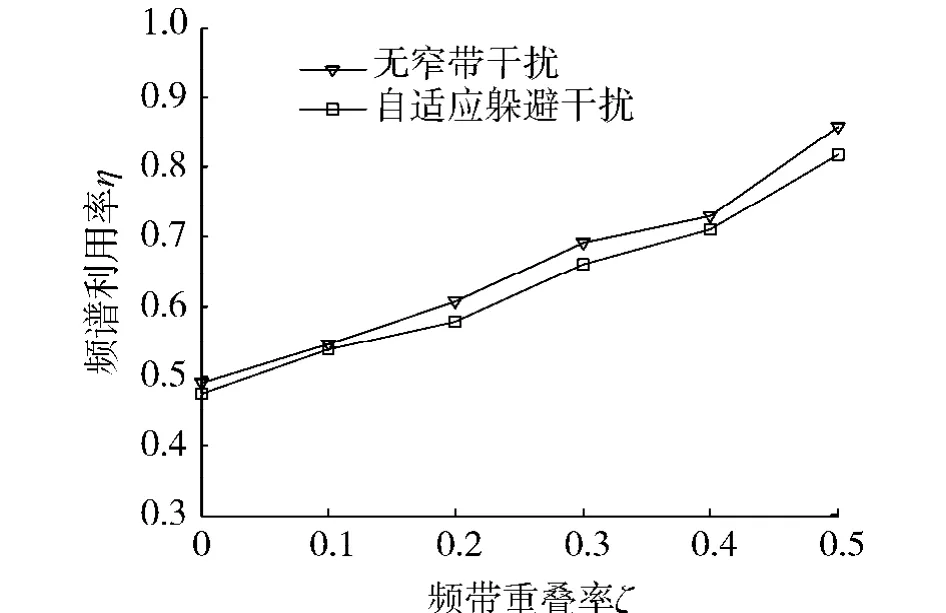
图3 频谱利用率Fig.3 Spectrum utilization efficiency

表1为目前文献中各种UWB脉冲波形的频谱利用率情况.从表中可以看出，传统的高斯、Rayleigh、Hermite、小波脉冲直接做UWB脉冲时，频谱利用率都很低，经过组合累加后的脉冲频谱利用率得到了很大的提高.本文提出的多频带自适应PSWF脉冲不但避免了窄带干扰，而且频谱利用率优于19个组合Chirp压缩脉冲，仅次于33个组合高斯脉冲.此外，多频带自适应PSWF脉冲的计算量小于组合高斯脉冲和组合Chirp压缩脉冲，利用该方法设计的脉冲在提高频谱利用率的同时，降低了系统的计算量.

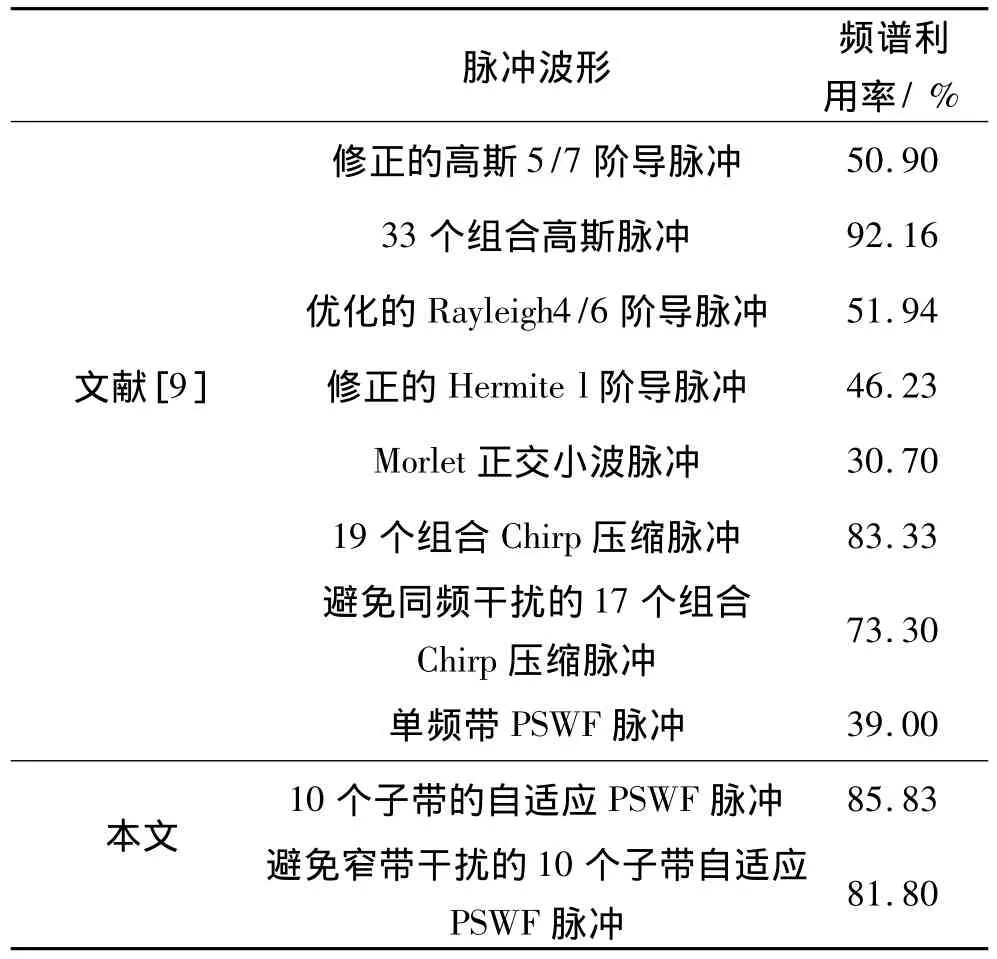
表1 UWB脉冲频谱利用率Table 1 Spectrum utilization efficiency of UWB pulse

3 多频带自适应脉冲性能分析

3.1 系统模型

发射UWB信号最常用和最传统的方式是利用信息数据符号对脉冲进行调制，除此之外，为了形成所产生信号的频谱，还要用伪随机序列对数据符号进行编码.本文采用二进制正交PPM-TH-UWB，发射端输出信号为

式中:cjTc定义了脉冲的相对于Ts整数倍时刻的抖动，ajε是由PPM调制引起的位移.

在二进制正交PPM-TH-UWB中，发射波形可以表示为

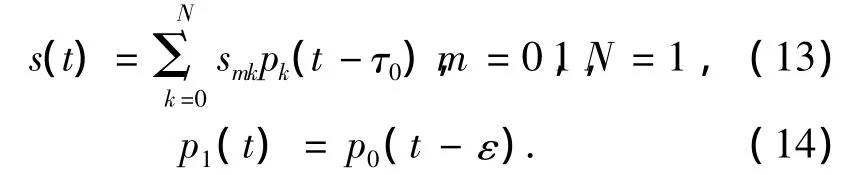
式中:τ0=jTs+cjTc，p0(t)和p1(t)表示信息比特“0”和“1”是每个脉冲携带的能量.

信号经过AWGN信道后，接收端接收到的信号可以表示为

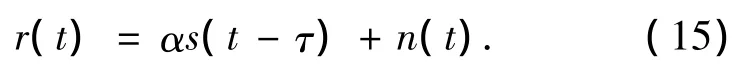
式中:信道增益α和信道延迟τ都取决于发射机和接收机之间的传播距离.本文假设接收机与发射机已经同步，令τ=0.

在接收端采用单相关器方案，接收信号送入相关器乘以相关掩模m(t)后，经积分器送入判决器进行判决［11］:

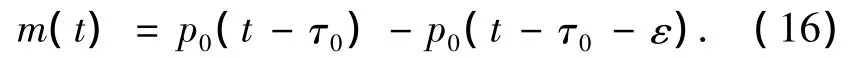
相关器输出的干扰信号功率谱为

式中:M(f)为m(t)的模，GN(f)为干扰信号的功率谱.

3.2 自适应脉冲性能分析

在传统的通信系统中，最常用的消除干扰的方法是设计滤波器.但是由于UWB信号带宽很宽，频带内的干扰源可能会很多并且数量和频率不确定.因此，单纯通过预先设计滤波器的方法很难消除干扰.可以通过系统参数和脉冲波形的选择来有效地消除干扰信号的影响，或与传统窄带系统实现共存［12］.

设频带内设窄带干扰带宽为BJ，中心频率为fJ，干扰功率谱为GN(f).则相关器输出的干扰功率谱为

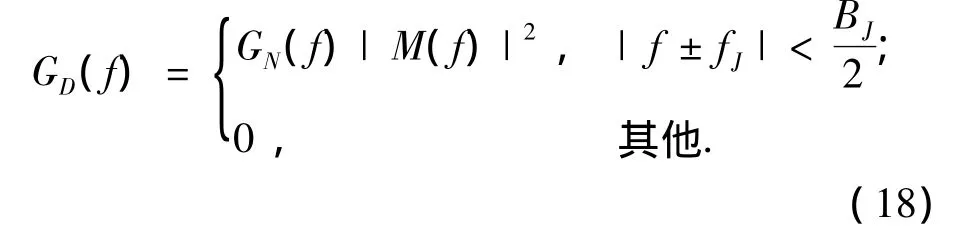
积分器输出干扰功率可表示为

此时，可调整脉冲波形参数，使P(f)在频带［fJBJ/2，fJ+BJ/2］内产生凹陷，则窄带干扰对超宽带系统的影响降到最低.

图4 窄带干扰下系统误码率Fig.4 BER with narrowband interference

图4为窄带干扰下的误码率曲线，假设背景噪声为高斯白噪声，信号与窄带干扰的信干比为－15 dB.从图4中可以看出，窄带干扰对系统性能造成了很大影响，信噪比的提高对系统误码率没有明显的改善.在系统自适应调整脉冲波形参数，撤销干扰频带内的子带脉冲之后，系统躲避干扰频带继续通信，此时，系统误码率与没有窄带干扰时的误码率相近，很好的抑制了窄带干扰对系统性能的影响.

4 结束语

在认知超宽带无线通信系统能够正确感知频谱环境并动态使用可用频谱空洞的前提下，无线电脉冲波形要解决两大问题:1)如何提高频谱利用率; 2)实现与现有通信系统的兼容.本文借鉴OFDM的思想，提出了一种能够动态地对频谱环境做出快速反应的自适应脉冲，减小了系统的计算量，提高了反应速度，实现了与现有窄带通信系统的共存.为了进一步提高频谱利用率，本文提出了频带重叠率的概念，对多频带自适应脉冲进行了修正，虽然增加了设计的复杂度，但可以将频谱利用率提高到85%以上.最后，对脉冲的抗干扰性能进行了分析，多频带自适应脉冲可以很好的抑制窄带干扰对系统性能的影响.在本文提出的生成自适应脉冲方法中，并没有考虑子带脉冲相位对累加结果的影响，应在后续的学习工作中进一步深入研究.

［1］MITOLA J，MAGUIRE G Q.Cognitive radio:making software radios more personal［J］.IEEE Personal Communications，1999，6(4):13-18.

［2］MOY C，BISIAUX A，PAQUELET S.An ultra-wide band umbilical cord for cognitive radio systems［C］//Proceedings of IEEE International Symposium on Personal，Indoor and Mobile Radio Communications.Berlin，Germany，2005: 775-779.

［3］GRANELLI F，ZHANG Honggang.Cognitive ultra wide band radio:a research vision and its open challenges［C］//Proceedings of IEEE 2nd International Workshop Networking with Ultra Wide Band Workshop on Ultra Wide Band for Sensor Networks.Rome，Italy，2005:55-59.

［4］贝尼迪特，吉安卡拉.超宽带无线电基础［M］.葛利嘉，朱林，袁晓芸，等译.北京:电子工业出版社，2006:131-167.

［5］梁朝晖，周正.基于小波的超宽带脉冲波形设计［J］.北京邮电大学学报，2005，28(3):43-45.

LIANG Zhaohui，ZHOU Zheng.Wavelet-based pulse design for ultra-wideband system［J］.Journal of Beijing University of Posts and Telecommunications，2005，28(3):43-45.

［6］GHAVAMI M，MICHAEL L B，HARUYAMA S，et al.A novel UWB pulse shape modulation system［J］.Wireless Personal Communications，2002，23(1):105-120.

［7］SLEPIAN D，POLLACK H O.Prolate spheroidal wave functions，Fourier analysis，and uncertainty［J］.Bell System Tech Journal，1961，40(1):43-64.

［8］JITSUMATSU Y，KOHDA T.Prolate spheroidal wave functions induce Gaussian chip waveforms［C］//Proceedings of IEEE International Symposium on Information Theory Conference.Toronto，Canada，2008:6-11.

［9］贺鹏飞.超宽带无线通信关键技术研究［D］.北京:北京邮电大学，2007:28-43.

HE Pengfei.Working out the key technologies of ultra wide band wireless communications［D］.Beijing:Beijing University of Posts and Telecommunications，2007:28-43.

［10］WU Xianren，TIAN Zhi，DAVIDSON T N.Optimal waveform design for UWB radio［J］.IEEE Transactions on Signal Processing，2006，54(61):2009-2012.

［11］朱刚.超宽带(UWB)原理与干扰［M］.北京:清华大学出版社，2009:92-115.

［12］岳光荣，葛利嘉.超宽带无线电抗干扰性能研究［J］.电子与系统学报，2002，24(11):1544-1550.

YU Guangrong，GE Lijia.System performance research of ultra-wide bandwidth radio in jamming environment［J］.Journal of Electronics and Information Technology，2002，24(11):1544-1550.