船舶在随机横浪中的全局稳定性

胡开业，丁勇，王宏伟，李积德

(哈尔滨工程大学 船舶工程学院，黑龙江 哈尔滨 150001)

倾覆是造成船舶严重事故的重要原因之一，历来受到造船界的极大关注.作为研究船舶倾覆的一种观点，从非线性动力系统稳定性的角度来研究船舶在波浪中的倾覆机理，已经引起了船舶科学工作者的广泛重视［1-4］.根据非线性动力学理论，除了局部分岔外，全局分岔也是导致系统稳定性丧失的途径之一［5］.

迄今为止，Melnikov方法是研究确定性动力系统全局稳定性的一种相当行之有效的方法，它通过构造系统的Melnikov函数，求解该函数的一阶零点来确定系统失稳时系统参数的阈值.Melnikov方法简单易行，而且还有可能解析求解，因此得到了广泛的应用.目前采用Melnikov方法对船舶在波浪中的全局分岔及稳定性的研究，多集中在研究外激励是规则波作用下的情况，如McCue等［3］、袁远等［4］、王迎光等［6］的研究工作，他们利用Melnikov方法对船舶在规则横浪作用下的全局稳定性进行了细致地研究，求解出了规则波中导致船舶出现混沌运动的外激励阈值.船舶在随机波浪中的运动稳定性的研究由于外激励的随机性使得分析和处理变得复杂，现有的研究多将外激励简化为白噪声［7-8］，采用概率密度函数研究船舶在白噪声激励下的随机横摇运动，然而实际的海浪则是具有有限的谱宽和给定的谱密度函数［9］，即为一有色噪声，显然白噪声模型与实际情况并不相符.

该文采用随机Melinikov方法对船舶在随机横浪中的全局稳定性进行了研究.研究了船舶在窄带随机噪声激励下的随机横摇运动，采用Melinikov均方准则确定系统混沌运动的临界参数条件，并用安全池法验证了噪声强度超过临界值时的船舶运动特性.

1 船舶在随机横浪作用下的横摇运动模型

假设横摇运动与其它运动方式不耦合，则船舶在随机横浪作用下的单自由度横摇运动微分方程可写为

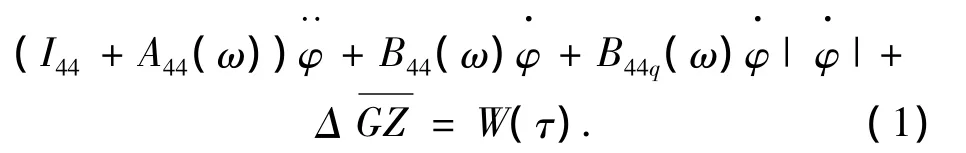
式中:I44为船舶横摇惯性矩;A44为附加惯性矩;B44为船舶横摇线性阻尼系数;B44q为船舶横摇非线性阻尼系数;Δ为排水量;W(τ)为随机横浪激励引起的力矩为船舶的静稳性臂，采用曲线拟合法可得

对于随机横浪外激励项W(τ)，目前有一些学者采用白噪声模型的简化方法，这种模型虽然在计算和分析处理时较为方便，但由于白噪声模型具有无限谱宽，而实际海况下随机波浪激励是一窄带随机过程，显然白噪声模型并不能很好的模拟船舶在随机横浪中所受到的实际外激励，虽然白噪声可通过滤波器过滤后变为一有色噪声，但增加滤波器后却大大增加了这一随机非线性系统的分析和求解的难度.该文通过计算分析发现，采用一种有界随机噪声模型可以模拟船舶在随机横浪中所受的随机外激励，无需增加滤波器即可直接分析船舶在该有界噪声下的随机运动特性.采用有界随机噪声法不仅可以较好的模拟出船舶在随机波浪中所受的随机外激励，对该随机系统的稳定性分析也变得较容易，下面介绍该有界噪声模型.

该有界噪声是一个具有随机频率与相位的协和函数［10］，其幅值为常数，表示为

式中:Ω表示中心频率，σ表示频率的随机扰动强度，B(τ)是标准Wiener过程，Γ是在［0，2π)上均匀分布的随机相位.

ξ(τ)的谱密度为

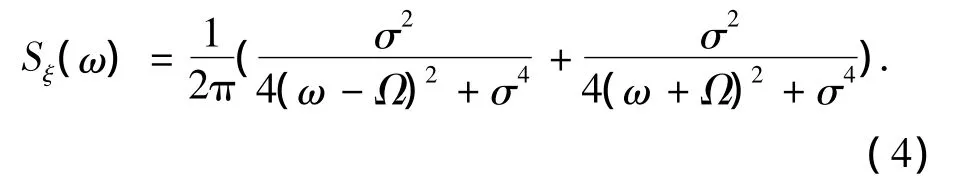
船舶在随机横浪中所受的随机外激励W(τ)主要由于随机波浪作用于船体产生的，对于随机波浪一般采用波能谱的形式进行描述，目前已有多种形式的波能谱表达式［9］，如纽曼谱、P-M谱、ITTC单参数及双参数谱、JONSWAP谱等，不同的波能谱公式均为对某一特定海域海浪能量分布的近似，其结果是有一定差别的，因而不同波能谱公式均有一定的适用范围，但不同形式的波能谱均属窄带谱，通过调整参数，均可被该有界噪声模型近似模拟.以P-M谱为例，通过计算可以发现，式(4)所描述的有界噪声模型的谱密度即可近似模拟P-M谱，图1是σ= 0.64，Ω=0.57时有界噪声谱密度曲线与有义波高为5 m时的P-M谱的谱密度比较图，从该图可以看出，在随机波浪所在的主要频率区间，随机噪声谱与波能谱曲线吻合良好，虽然在波浪频率较小时，随机噪声谱密度值较波能谱值偏差较大，但由于该频率段在实际波浪中出现的概率较小，因此将船舶在随机波浪中所受到的随机波浪外激励W(τ)考虑为式(3)所描述的有界噪声模型在实际应用中还是具有较高精度的.

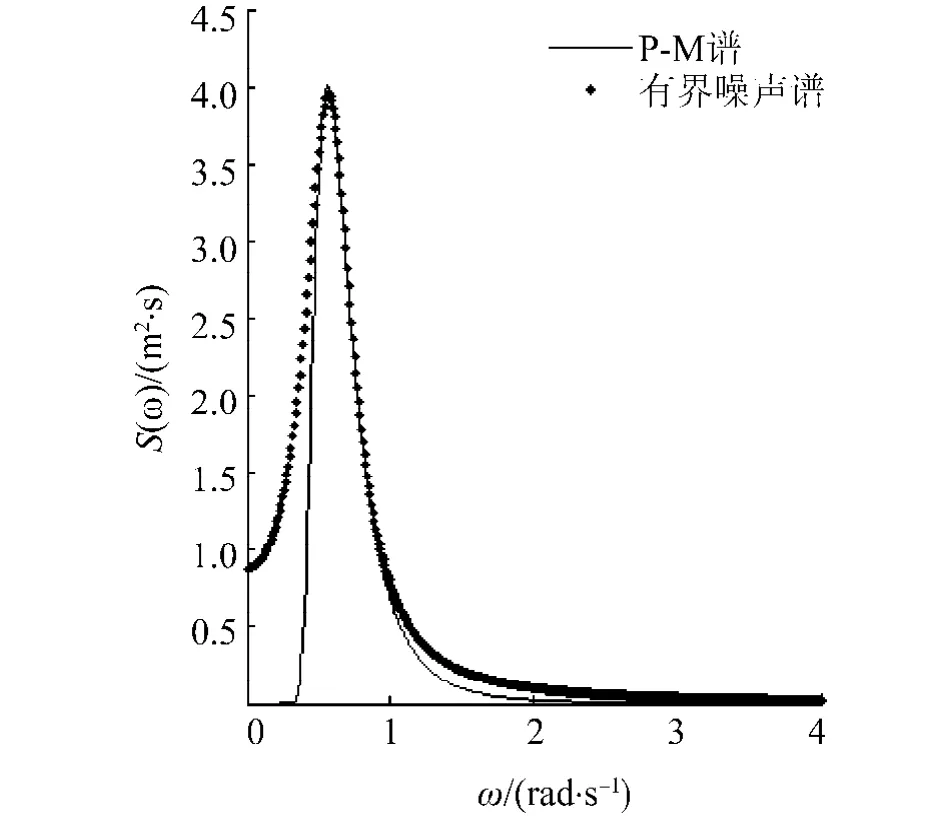
图1 有界噪声谱与P-M谱Fig.1 Bounded noise spectrum and P-M spectrum

将式(1)中随机横浪外激励项W(τ)改写为有界噪声ξ(τ)的形式，则式(1)改为

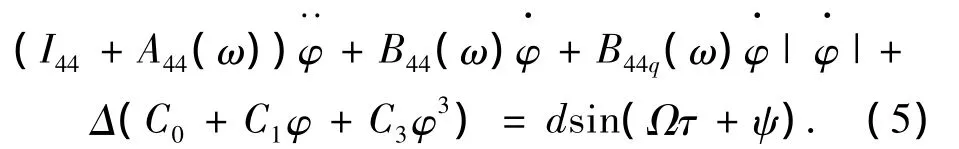
式中:d为噪声强度，当ψ=0时，则方程(5)成为规则波作用下船舶横摇运动非线性微分方程.将式(5)无因次处理后，得

式中:x=φ，t=ω0τ，ω0

2 随机Melnikov均方准则

Melnikov方法是基于摄动分析给出受到小扰动的可积系统出现横截同宿(异宿)轨道的解析条件，作为预测系统出现混沌运动的必要条件.由庞加莱理论［5］知，如果Melnikov函数有简单零点，则系统稳定流形与不稳定流形横截相交，一旦相交就有无数次相交，吸引子的相空间发生形变，不停地伸缩与折叠，从而产生Smale马蹄意义下的混沌.对于随机系统，需要从概率或统计意义上讨论随机Melnikov过程是否具有简单零点，因而有随机Melnikov均方准则［10］.

对于噪声扰动下的单自由度哈密顿系统，其运动方程为

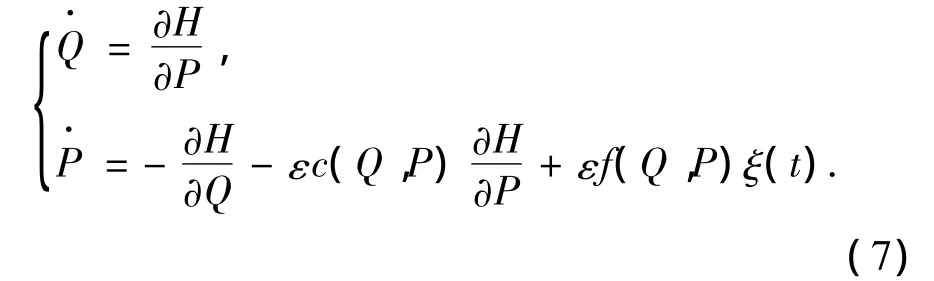
式中:H=P2/2+U(q)，ξ(t)是随机外激励.设相应的哈密顿系统有一个被同宿轨道(q0(t)，p0(t))连接的双曲鞍点.则式(7)的Melnikov过程为

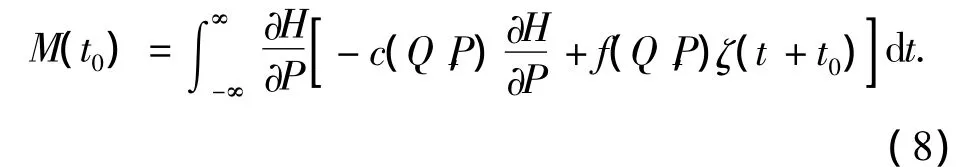
式中:Q=q0(t)，P=p0(t).鉴于E［ξ(t)］=0，随机Melnikov过程的均值为

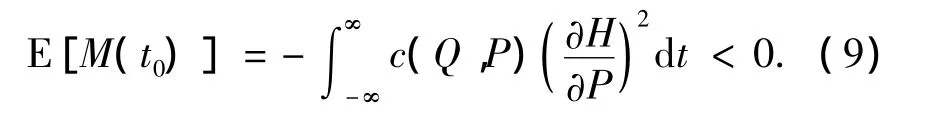
显然，当c(Q，P)＞0时，随机Melnikov过程在均值意义上不可能有简单零点，从而系统(7)在均值意义上不可能出现混沌.随机Melnikov的均方值为

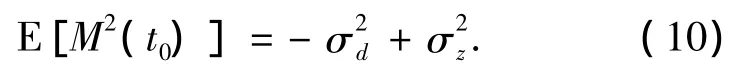
式中:

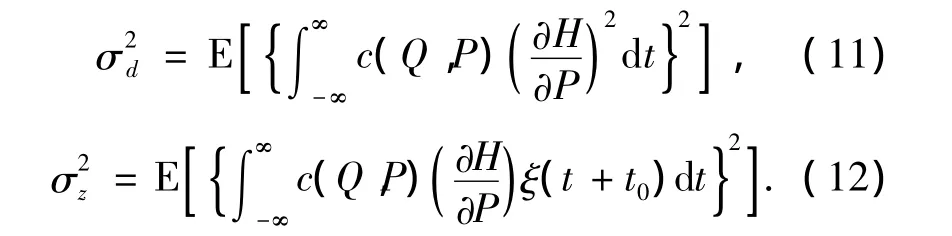
式(12)中的积分:

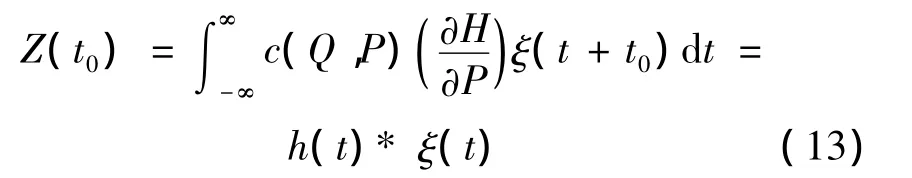
是一个卷积分，其中:

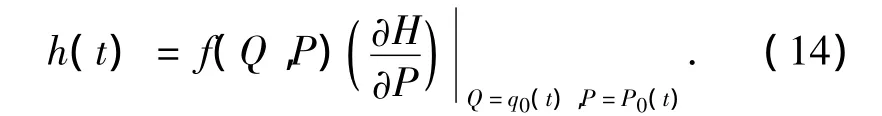
可看成一个脉冲响应函数.因此

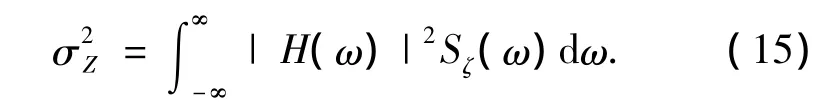
式中:H(ω)是h(t)的Fourier变换，即频率响应函数，Sξ(ω)为ξ(t)的谱密度.随机Melnikov过程在均方意义上有简单零点的条件，即系统出现混沌的准则为

下面利用该准则来分析船舶在随机横浪中的全局稳定性，将式(6)改写成形如式(7)的2个一阶微分方程的形式:

方程(17)是一个可积Hamilton系统，对于无扰动的系统ε=0，有

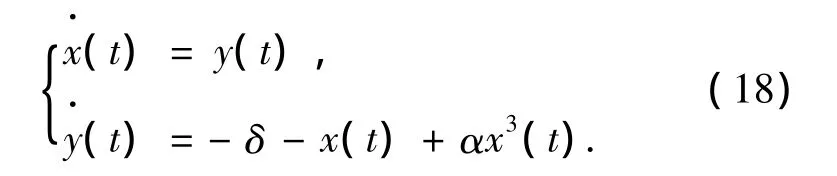
解上述微分方程，可得

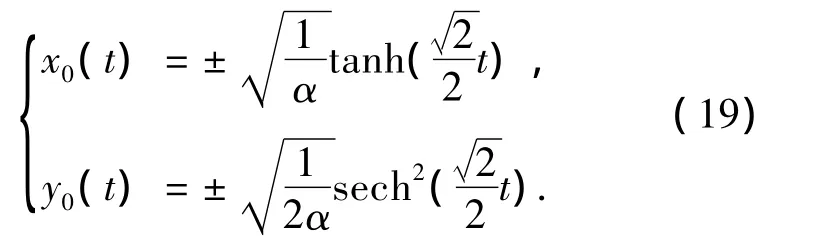
式中:“+”代表异宿轨线的正轴部分，“－”代表异宿轨线的负轴部分，这条轨线是区分船舶静水中安全与倾覆的界限.

式(17)的随机Melnikov函数为

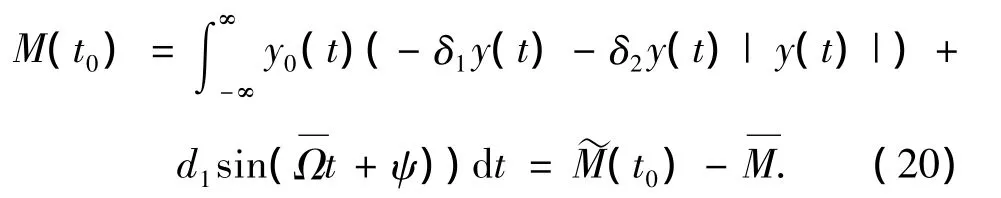
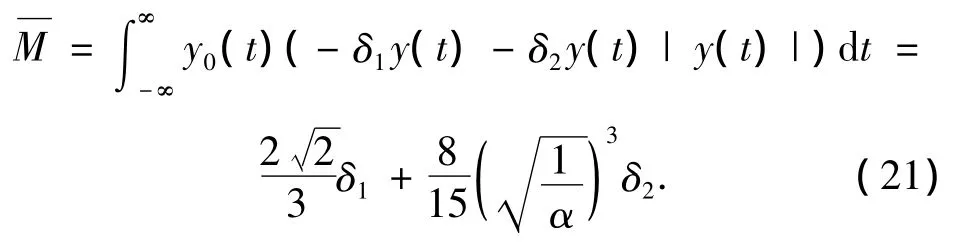
由式(11)得

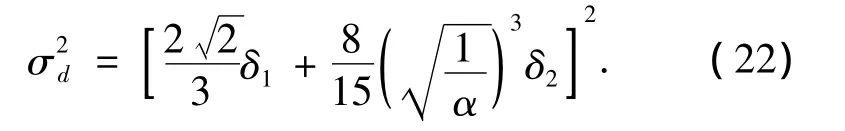
由式(14)、(19)可得

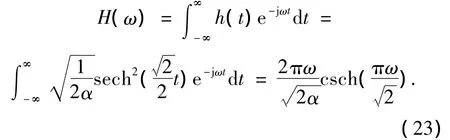
将式(4)、(23)代入式(15)，即可计算出

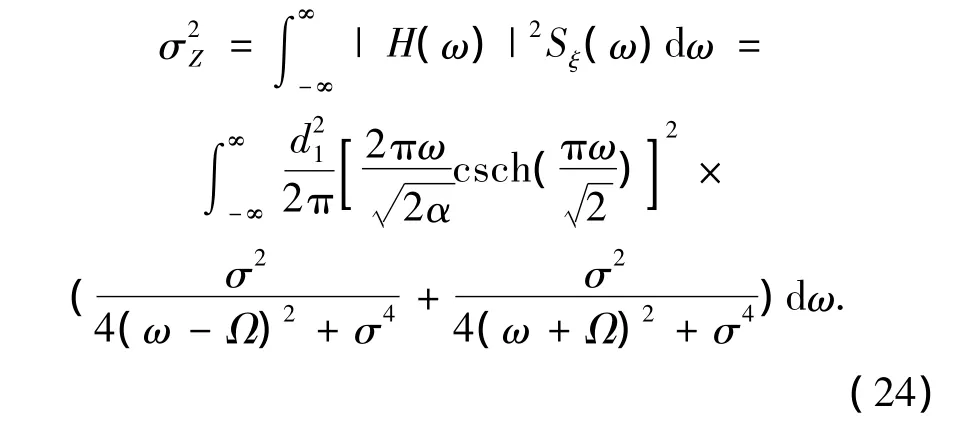
3 算列分析

以一Patti-B型船为例［11］，计算该船在随机横浪中的全局稳定性，该船船型参数见表1.

表1 Patti-B型船船型参数Table 1 List of parameters for Patti-B

根据表1的参数，计算可得方程(6)的系数为εδ1=0.003 7，εδ2=0.067 2，α=3.135 5.由式(22)、(24)可确定出σ2d和σ2z，代人到式(16)随机Melnikov均方准则，即可计算出该型船均方意义上的简单零点条件为d1=0.005 6.即该船在有界噪声激励幅值小于0.005 6时运动稳定，而有界噪声激励幅值大于0.005 6时该船可能会出现不稳定的混沌运动，影响船舶的安全性.

由于Melnikov函数具有简单零点只是随机非线性系统出现混沌运动的必要条件而不是充分条件，为验证该方法的正确性，分别选取有界噪声幅值小于混沌临界值和大于混沌临界值的激励，计算系统的安全池［12］来分析其随机运动特性.图2是当有界噪声激励幅值d1=0.005时的安全池，从图2可以看出，当有界噪声激励幅值小于临界值时，系统具有完整的安全池，说明此时的船舶运动是安全的，而当有界噪声激励幅值d1=0.007超过临界值时，系统的安全池出现破损(见图3)，说明此时船舶的运动是不安全的.

假设某船具有较大的阻尼系数，其εδ1=0.006，通过式(16)的计算可得其均方意义上的简单零点条件为d1=0.006 1，对比Patti-B型船的计算数据可以看出，增大船舶阻尼可以增加船舶航行的安全域.

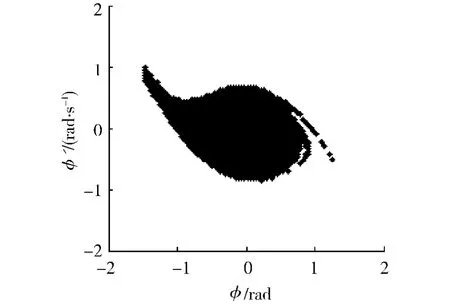
图2 安全池(d1=0.005)Fig.2 Safe basin for d1=0.005

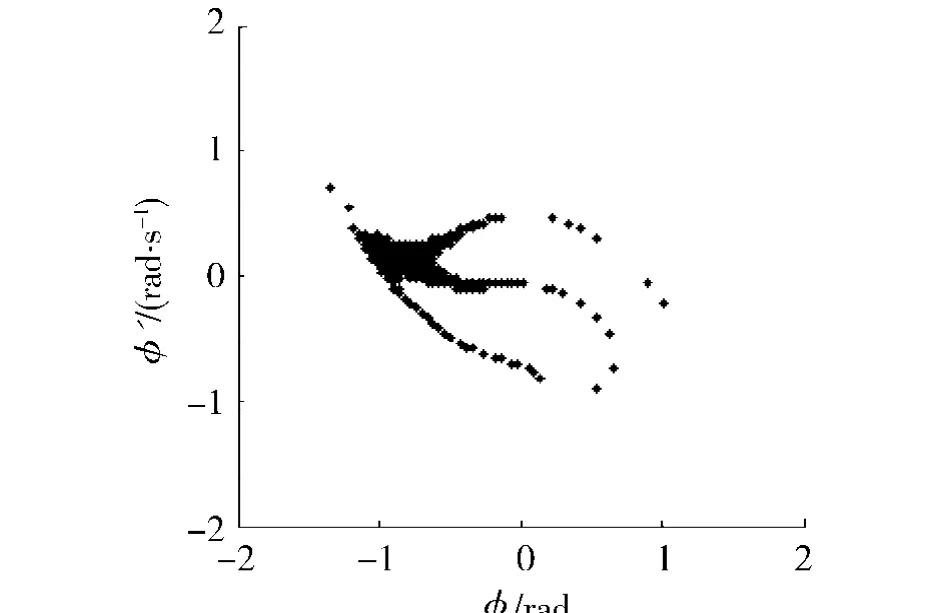
图3 安全池(d1=0.007)Fig.3 Safe basin for d1=0.007

4 结论

该文从非线性随机动力系统分岔的角度来探索船舶在随机波浪中的奇异倾覆机理，通过随机Melnikov对有界噪声激励下船舶随机横摇运动的全局稳定性进行了分析，得到了导致船舶运动稳性丧失的外激励阈值，该文的研究表明:

1)可以采用有界噪声模型近似模拟船舶在随机横浪中实际所受到的外激励;

2)船舶在随机横浪中航行时，在随机激励幅值超过某一临界值时，即会产生不稳定的横摇运动而导致船舶倾覆，随机激励幅值的大小反映了船舶所在海域的恶劣程度，因此船舶应尽量避免在恶劣海况下行驶;

3)增加船舶的阻尼可以提高船舶航行的安全域.

该文的研究可为船舶在随机海浪中的安全营运提供参考.

［1］HU Kaiye，DING Yong，WANG Hongwei.Chaotic roll motions of ships in regular longitudinal waves［J］.Journal of Marine Science and Application，2010，9(2):208-212.

［2］胡开业，丁勇，王宏伟.船舶在随机纵浪中参数激励横摇稳定性研究［J］.船舶力学，2011，15(1-2):11-16.

HU Kaiye，DING Yong，WANG Hongwei.Stability analysis of the parametrically excited ship rolling in stochastic longitudinal waves［J］.Journal of Ship Mechanics，2011，15 (1-2):11-16.

［3］WU W，MCCUE L S.Application of the extended Melnikov＇s method for single-degree-of-freedom vessel roll motion［J］.Ocean Engineering，2008，35:1739-1764.

［4］袁远，余音，金咸定.船舶在规则横浪中的全局稳定性［J］.振动与冲击，2003，22(1):85-87.

YUAN Yuan，YU Yin，JING Xianding.Global stability of ship motion in regular beam seas［J］.Journal of Vibration and Shock，2003，22(1):85-87.

［5］刘延柱，陈立群.非线性振动［M］.北京:高等教育出版社，1998:286-295.

［6］王迎光，谭家华，薛雷平.用迈尔尼可夫法分析海洋结构物动态稳性［J］.海洋工程，2009，27(1):77-82.

WANG Yingguang，TAN Jiahua，XUE Leiping.Analyzing an ocean structure＇s dynamic stability by using Melnikov method［J］.The Ocean Engineering，2009，27(1):77-82.

［7］刘利琴，唐友刚，吴志强.横浪中船舶的随机横摇运动［J］.工程力学，2004，25(6):204-208.

LIU Liqin，TANG Yougang，WU Zhiqiang.Stochastic chaotic motion of ships in beam seas［J］.Engineering Mechanics，2004，25(6):204-208.

［8］GU J Y.Nonlinear rolling motion of ship in random beam seas［J］.Journal of Marine Science and Technology，2004，12(4):273-279.

［9］李积德.船舶耐波性［M］.北京:国防工业出版社，1987: 24-28.

［10］朱伟秋.非线性随机动力性与控制——Hamilton理论体系框架［M］.北京:科学出版社，2003:267-320.

［11］JIANG C B.Highly nonlinear rolling motion leading to capsize［D］.Michigan:University of Michigan，1995:9-15.

［12］李远林.风暴中船舶安全池破损问题［J］.中国造船，2004，45(1):14-18.

LI Yuanlin.The erosion of ship safe basin in storms［J］.Shipbuilding of China，2004，45(1):14-18.

［13］袁远，余音，金咸定.船舶在随机横浪中的奇异倾覆机理［J］.船舶力学，2004，8(1):44-50.

YUAN Yuan，YU Yin，JING Xianding.Capsize mechanism of ships in random sea［J］.Journal of Ship Mechanics，2004，8(1):44-50.

［14］刘利琴，唐友刚，郑宏宇.随机横浪中船舶倾覆概率的时域分析方法［J］.天津大学学报，2006，39(2):165-169.

LIU Liqin，TANG Yougang，ZHENG Hongyu，et al.A-nalysis method of capsizing probability in time domain for ships in random beam waves［J］.Journal of Tianjin University，2006，39(2):165-169.

［15］WANG Yingguang，TAN Jiahua.Global geometric analysis of ship rolling and capsizing in random waves［J］.China Ocean Engineering，2007，21(4):577-586.

［16］唐友刚，谷家杨，郑宏宇，等.用Melnikov方法研究船舶在随机横浪中的倾覆［J］.船舶力学，2004，8(5):27-34.

TANG Yougang，GU Jiayang，ZHENG Hongyu，et al.Study on the ship capsize in random beam seas using Melnikov method［J］.Journal of Ship Mechanics，2004，8 (5):27-34.

［17］赖志昌，金鸿章，李国斌，等.随机海浪作用下的船舶横摇减摇预报方法［J］.哈尔滨工程大学学报，2001，22 (3):13-16

LAI Zhichang，JIN Hongzhang，LI Guobin，et al.Prediction of roll stabilization of ship in random wave［J］.Journal of Harbin Engineering University，2001，22(3):13-16.