透射电子显微镜中物镜光阑的作用与影响

杨彦杰，董全林*，袁水平，于成交，张春熹，许春兰

(1.北京航空航天大学微纳测控与低维物理教育部重点实验室，北京100191；2.北京电子科技职业学院，北京100036)

透射电子显微镜一个非常重要的应用就是利用衍射模式观察晶体样品的衍射谱，从而可以获得样品的晶体学信息。由于物镜球差的影响晶体试样的各衍射斑的像在叠加时不能完全重合，从而导致像的衬度不好进而影响了所成像的分辨率。为了消除这种影响，可以在物镜后焦面上放置一个光阑称为物镜光阑，由于物镜光阑是透射电镜中振幅反差的来源，因此也称反差光阑或衬度光阑。用物镜光阑选择某一衍射斑来成像，这样就不存在衬度叠加与像相互不重合的问题，从而提高像的衬度和分辨率[1]。

本文从几何电子光学理论出发，分析并计算了与物镜光阑相关联的像差和衍射对电镜分辨率的影响，并根据傅里叶电子光学理论研究了物镜光阑对透射电镜电子频谱滤波作用。

1 与物镜光阑相关的像差和衍射

物镜是电镜中最重要的部件。为了获得高的分辨本领，透镜的球差、色差和象散等应尽可能减小。其中对电镜分辨率本领影响最大的是衍射效应和球差。色差的影响可以通过提高加速电压和透镜电流的稳定度以及适当的调配透镜的极性，可以将其控制在分辨本领要求的范围内。下面我们讨论物镜光阑对衍射效应、球差和色差的影响。

1.1 物镜光阑的衍射效应对分辨率的限制

根据光学衍射理论，一个圆孔光阑的衍射强度分布可以表示为[2]：

式中，I0为中心光斑的能量，J1（r）为一阶贝塞尔函数。根据瑞丽判据可以得到光学显微镜由衍射效应限制的分辨率极限为：

式中，λ为入射光波的波长，n物方折射率，u为物方孔径角。与光学显微镜类似，在傍轴情况下电子光学系统的成像性质与光学系统相似，在其它像差可以忽略的情况下，电子显微镜的分辨本领由衍射效应限制，其分辨率公式可表示为：

图1 物方孔径角与物镜光阑的关系

由(3)可知，在忽略其它像差对分辨率的影响的情况下，降低电子束波长和增加物方孔径角都可以提高电镜的分辨本领。其中降低电子束波长可通过提高加速电压Vγ来实现，增大物方孔径角可以通过增大物镜光阑的半径来实现。

1.2 物镜光阑对球差的影响

在电子显微镜的像差中，球差的影响最大而且没有简便的方法消除。在电磁透镜中，由于轴上磁场对电子的折射能力比离轴远的磁场差，所以，一个物点上发出的大孔径角的电子汇聚的快一些，小孔径角的电子汇聚的慢一些，于是在原来理想的像点附近形成了一个弥散的小球，这种像差称为球差。如图2所示。

图2 球差及在不同平面上的散射斑大小

在实际透镜中由于受物镜光阑的限制，电子射线存在一个包络线使图形形成一个圆盘，在高斯像平面上圆斑半径为r＝Bu3。成像上的这种球差影响了电镜的分辨本领。由球差限定的最小物方分辨距离为：

式中，Cs为球差系数，对于给定的透镜它为常数。u为物方孔径角。由(4)式知，采用大的孔径角可引起大的球差，因此可以通过减小光阑尺寸的方法来减小物方孔径角，从而提高分辨率。

1.3 物镜光阑对色差的影响

在磁透镜中，色差主要是由电子速度的变化产生。色差与傍轴条件无关，只与电子速度波动有关。造成电子波动的原因很多，如透过样品时电子能量的损失、加速电压和激励电流的波动等。色差可由下式表示：

1.4 最佳孔径角

根据物镜光阑对衍射、球差和色差的影响，综合考虑，同时存在球差和衍射时引起的散射圆斑半径的平方假定为两者的平方和，即：

由条件dr/du＝0得出自家孔径角为：

同时存在色差及衍射引起的散射斑半径由下式决定：

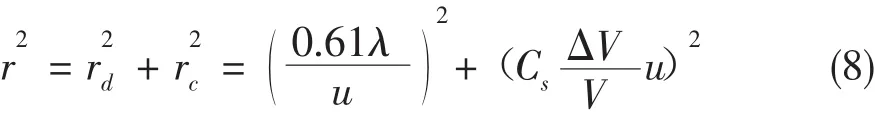
由条件得出自家孔径角为：

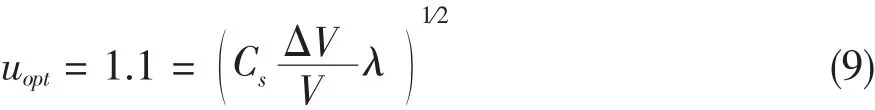
对试样上发出的电子的角度分布做不同的假定，并按照衍射理论作详细计算后，得出的结果和(7)(9)在系数上会略有不同。

在实际的电子光学系统中，根据实际的设计情况可以计算出电子光学系统的最佳孔径角，从而进一步得出在最佳孔径角下的理论分辨率。

2 物镜光阑场深和焦深的影响

若物点在距离为D的范围内沿轴移动，其像在P1到P2间移动时同样是清晰的，则称距离D为透镜的场深；在固定物点的情况下，像面沿轴移动仍能保持清晰的范围称为焦深。图3给出了场深和焦深以及光阑对他们的影响的示意图。

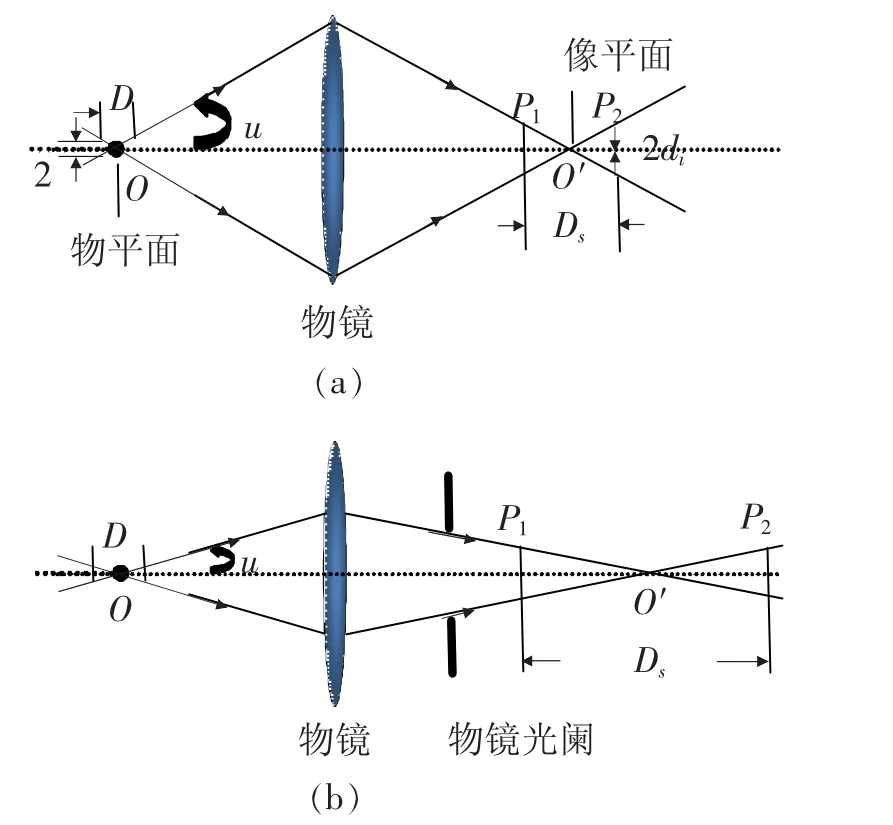
图3 场深和焦深以及物镜光阑的影响

我们知道，任何一个透镜都不能完善成像，只能把物点成像为光斑，其半径就是透镜的分辨本领。图3(a)中物点O成像为像点O′，由于物镜的球差像点O′变为半径为di的弥散圆斑其半径为M0d(这里M0为物镜的放大倍数，d为还原到样品的最小分辨距离)。根据成像公式场深D和焦深Ds可以表示为：

如果u＝2×10－3rad，d＝10A°，则D ＝1 mm。这意味着对于分布在厚度为1 mm范围内的样品细节均能获得10A°的最小分辨距离。另外调焦时，物面位置可以允许有1 mm的误差而不影响电镜的分辨率。

物镜的放大倍数一般在100～200之间，由(11)式可知，焦深要比场深大M20倍。如果物镜放大倍数为100，场深为1 mm则焦深为1 cm。事实上，电镜采用的是多级放大，假设物镜后的光学系统总放大倍数为1000，那么可以算出最终像平面的焦深为1000 m。这使我们可以把荧光屏感光板或照相机胶片放置在投影镜下的任何位置，并且像都是清晰的。只是位置不同，放大率不同。从图3(b)中可以看出，加上物镜光阑后，孔径角会缩小，场深和焦深都显著增加。

3 物镜光阑对电子频谱的影响

根据阿贝成像原理，透射电镜的成像过程可以看作是电子的两次衍射过程，第一次为分频，受试样调制的电子波被分解为不同的频谱分量，在物镜的后焦面上得到其衍射谱。第二次为合成，不同的频谱分量在像平面上合成物的像。因此，可以通过物理手段在频谱面上改变物体的频谱分布来达到改变和处理图像的目的[3]。

在观察晶体试样时，平行电子束照射在晶体上时电子发生衍射，并且遵从布拉格公式：

式中，n为衍射级数，λ为电子束波长，d为晶面间隔，θB为衍射角。设物镜足够大即衍射频谱全部通过物镜而没损失，从而在物镜的后焦面上得到晶体试样的频谱分布。

则通过光阑后的电子波频谱分布为：

式中，

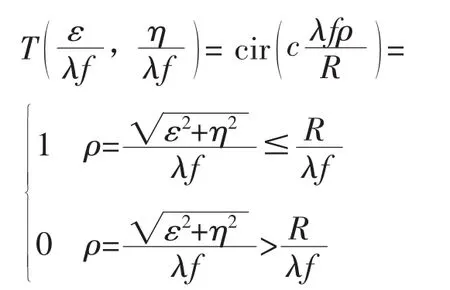
这是一个圆柱体，其截至频率为：

由公式(13)和(14)可以看出，在频率域中只有小于物镜光阑截至频率的空间频谱才能通过光阑参与成像。因此，物镜光阑也可以看作是一个低通滤波器，它对电子频谱起到了滤波的作用。也就是说，只有在傍轴附近一定的区域内的电子束可以通过，参与成像的频谱是有一定范围的。由于物镜光阑挡住了大角度的散射电子，而这些大角度的电子束是带有高频信息的频谱，因此在成像时像的清晰度受到了影响。

4 总结

在本文中，首先综述了物镜光阑与影响透射电镜分辨本领的衍射、球差和色差的关系。在综合考虑了各种像差时得出了最佳孔径角的计算公式。最后通过傅里叶电子光学理论分析了物镜光阑对电子频谱的影响。

通过分析，我们在不同的实验中，出于不同的考虑对物镜光阑的要求也就不同。在观察薄样品是，这时衬度是由相位效应引起的，因此采用大的物镜光阑可以使样品上的细节信息得到反映。在观察以振幅衬度为主的样品是，为了得到较高的反差，需要用较小的物镜光阑，然而在得到较大的反差的同时增加了高频信息的损失，从而降低了分辨率。因此，在透射电镜的实际设计和使用中，需要考虑不同的情况来设计和选择物镜光阑的大小。

[1]姚骏恩.电子显微镜的现状与展望[J].电子显微学报，1998，17(6)：767-776.

[2]朱祖福，沈锦德，许志义，等.电子显微镜[M].北京：机械工业出版社，1980.

[3]潘尔达.电子显微镜中的物镜光阑对电子波频谱的影响[J].云南大学学报，1987，9(1)：35-37.

[4]陈文雄，西门纪业.基础电子光学[M].北京：北京大学出版社，1986.

[5]西门纪业，葛肇生.电子显微镜的原理和设计[M].北京：科学出版社，1979.