低能光子的量子引力“遗迹”效应

邵立晶，马伯强

(北京大学物理学院，北京100871)

随着人们对于各类对称性与对称性破缺的深入理解，以及量子引力理论发展的需要，物理学家开始考虑在极高能量下洛伦兹对称性存在着破缺的可能性。 倘若量子引力能标1.22×1019GeV下存在着洛伦兹破坏行为，那么，在低能下就会有微小的残留“遗迹”效应，比如说，对正则能动量色散关系E2＝p2＋m2会产生一个小的修正。进一步地，这修正将体现出低能下丰富多彩的量子引力现象学，为量子引力理论的实验探索提供了一个宝贵的窗口[1]。

虽然洛伦兹破坏即使存在，修正项也会由于普朗克物理的压低而很小，可是，令人感到幸运的是，自然界存在一定的机制来“放大”量子引力的效应，如，长基线的宇宙距离的传播，超精准地球实验的测量等。 同时，如今的地球实验与天文观测的技术发展，在精度上已部分达到探测量子引力“遗迹”的能力，并在未来的实验装置中将有更好的改进。这些观测可用来探测与约束洛伦兹破坏效应，并以此来区分、检验或约束量子引力理论。

本文讨论了在量子引力唯象学领域最热门的“标准模型拓展”以及在此框架下的光子的色散关系。进一步地，文章研究了量子引力在天体物理的高能光子领域上所体现出的效应，并与最新的实验相结合，对量子引力理论进行一定的检验与约束。

1 量子引力理论与光子的色散关系

不同的量子引力理论给出了不同的预言，如弦论[2]、时空泡沫理论[3]、圈引力理论[4]和非对易几何场论[5－7]等。 一般来说，它们都会给出对标准的能动量色散关系E2＝p2＋m2的修正，可是具体的修正项与修正行为有所不同，所以能够从实验上加以区分与鉴别。

对于洛伦兹破坏物理的描述，最直接与最有效的出发点就是把洛伦兹破坏项纳入到标准模型这个“有效量子场论”的框架中。 Colladay和Kostelecky做了这方面最成功的尝试，系统地发展了“标准模型拓展”[8－9]，这是 SU(3)⊗SU(2)⊗U(1)对称性下的标准模型的最小扩展。扩展的拉氏量中引入了直接破坏洛伦兹对称性的“洛伦兹破坏项”。这些项可以看成是从高能标到低能标时“对称性自发破缺”而导致张量场获得真空期望值，并进一步与标准模型中的场量耦合。模型保留了标准模型中的很多好的性质，如规范不变性、能动量守恒、洛伦兹协变性、微观因果性、能量的正定性和反常相消等。而且，由于这个拓展的理论并没有离开大家比较熟悉的量了场论的框架，理论的预言与实验观测检验也比较方便，所以，很多研究集中于此。

Colladay和Kostelecky初步研究的“标准模型拓展”是可重整的有效场论，他们的做法十分直观有效。他们把张量场由于洛伦兹自发破缺导致的真空期望值作为拉氏量中的常数系数，通过引入它们与标准模型的场量的耦合，这些项将展现出洛伦兹破坏的物理，例如，对于光子场而言，所有可重整的洛伦兹破坏算符可通过对称张量（kF）κλμν与反对称张量（kAF）κ引入。具体来说，纯光子部分的拉氏量为[8，9］，

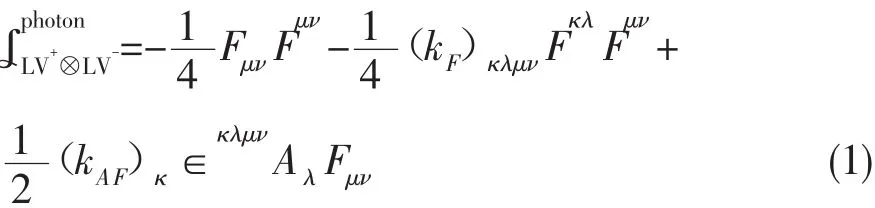
其中，(kF)κλμν部分是 CPT 为正的，而(kAF)κ部分破坏了CPT对称性，是CPT负的。要注意的是，这个拉氏量中的系数kA与kAF，虽然也带有洛伦兹指标，但与其他的场量不同，它们是破坏了洛伦兹协不变性的。从形式上来看，可以很容易看出它们保持了理论的洛化兹协变性；直观地说，也就是保持了上下指标的有效收缩。所以，新引入的洛伦兹破坏项，在粒子的洛伦兹变换下，它们作为背景常场量，是不变的，而对于坐标第的变换，它们是与其他的张量一样变化的；这就是引入洛伦兹破坏项的关键点。同样，通过与上面一样的方法，也可以引入标准模型的其他成分[8－9]。

其后，Myers，Pospelov[10]和Mattingly等人系统地研究了不可重整的“标准模型拓展”。不可重整的理论的好处在于，在拉氏量中引入的修正项是直接受到普朗克能量压低的，人而能够更加自然地给出“微小”的洛伦兹破坏效应，在无量纲耦合系数量级为O(1)情况下，能够与实验和观测没有严重的冲突。不可重整的理论给出了更好的普朗克能标压低的机理。所以，近些年的研究，对于不可重整的量子场论也有了很多的涉及与讨论。

对于质量量纲为5-维的标准模型拓展，依据拉氏量在CPT变换下的行为，我们可以把这些5-维的不可重整项分为CPT为厅和CPT为偶两大类[11]。CPT为厅的光子修正项可写为[11－12]

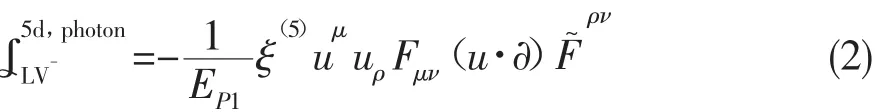
其中的u是个固定的类时四矢量，表明了特殊的参考系方向，F～的定义为F～μν=∈μνρλFρλ/2；PR，L=(1±γ5)/2是左右手投影算符，Dμ＝∂μ＋ieAμ是QED中的协变微商；ξ，δR，L和ζR，L是量级为 O(1)的洛伦兹破坏系数；另外，LV-中的“-”号表示CPT为奇，后面类似的“+”号表示CPT为偶。CPT为偶的5-维的光子修正项并不存在，即另外，Mattingly给出了空间旋转不变情形下的6-维质量量纲的洛伦兹破坏的光子项[11－12]

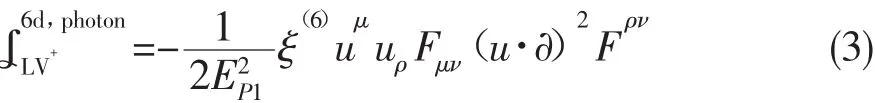
通过5-维，或者6-维的拉氏量，我们可以得到相应情况下的光子能动量色散关系[12]

其中，n＝5表示5－维情况，n＝6表示6－维情况。在有效场论中，这就意味着5－维洛伦兹破坏项会导致双折射现象[13]。

2 光子传播时延

可以看到，在量子引力理论中，传统的色散关系可能会受到微小的修正。正是这微小的修正，衍生出了丰富多彩的洛伦兹破坏唯像学研究。在洛伦兹破坏修正的色散关系下，我们假设粒子速度v＝∂E(p)/∂p仍旧成立的话，那么，对于光子来说，我们就会有非恒定的光速，写成泰勒展开形式，有

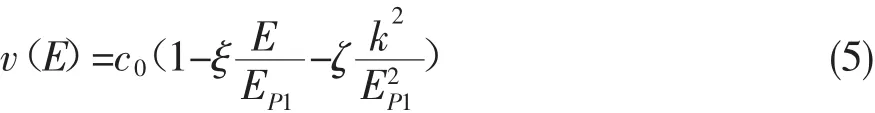
其中，ξ和ζ是洛伦兹破坏产生的修正系数，对应于前面理论中的洛伦兹破坏参数。现在的实验与观测倾向于排除它们为负数的情况。如果它们是正数的话，就意味着越高能量的光子，速度越慢。而另一方面，如果ξ≠0的话，那么，ζ项的修正完全可以忽略。

由于光子的速度对于能量有所依赖，那么对于同时发射的不同能量的光子，经过一定的距离所消耗的时间会有所不同。我们这里感兴趣的是宇宙学距离上的光子传播。考虑到宇宙的膨胀效应，能量为Eh的“高能光子”相对于能量为E1的“低能光子”有个洛伦兹破坏导致的时间延迟[14]，

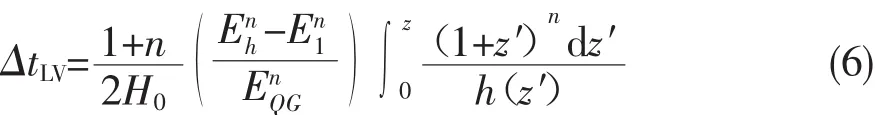
下面考虑这个效应在γ-暴 (GRB)观测中的应用。 近来由于观测上的进步，如Swift卫星与Fermi卫星等的上天，GRB的研究有了实质性的突破进展。特别是，Fermi卫星的LAT装置的探测能量达到300 GeV以上，使得GRB的高能研究成了一个有坚实观测实事基础的领域。同时，GEB的高能端的研究也能用来检验与约束新物理，洛伦兹破坏就是其中著名的一例。Amelino－Camelia等人[3]首先提出了通过伽玛暴的精细的光变曲线与宇宙学距离的放大来检验洛伦兹破坏效应导致的光速对于能量的依赖关系。这里主要的出发点是从方程(6)引入的洛伦兹破坏延时，来看看是否真的在伽玛暴的光变曲线中存在。

可是，由于伽玛暴的光变曲线非常复杂，所以高能光子对于低能光子的延时的测量是个比较不确定的事情，容易引入人为的偏见，也可能存在仪器测量上的不确定性。就比如在GRB 090510的讨论中，就涉及了各种可能用来确定洛伦兹破坏延时的可能性[15]。为了讨论上的一致性，选取了Fermi LAT中的最高能量光子相对于Fermi GBM装置的触发光子的延时。由于GBM装置的触发阈值为0.1 MeV，而最高能量的光子在几个或者几十个GeV的量级上，所以，在方程(6)中，可以把E1近似取为零[17]。

Fermi LAT装置由于只能探测到非常高能量的伽玛暴，所以它大致上每个月能够探测到一例。另外，在分析中又需要伽玛暴的红移（距离）信息，而红移的测量又是需要其他的天文观测装置的及时跟进。所以，Fermi LAT测量到的伽玛γ－暴中满足我们需要的并不多。后面的讨论基于有距离信息z的4个Fermi LAT的高能伽玛暴，GRB 080916C， GRB 090510， GRB 090902B， GRB 090926A。

假设观测到的高能光子对于低能光子的延时效应全部由洛伦兹破坏效应提供，即

那么，根据方程(6)，可以分别得到洛伦兹破坏对于能量是线性依赖以及平方依赖两种情况下的洛伦兹破坏能标EQG，L和EQG，Q。从计算结果中我们看到[17]，不同的伽玛暴的延时效应给出的洛伦兹破坏的能标是不同的，甚至在数量级上有所差异。如，使用最小二乘法线性回归后，可以看到，线性能量依赖情况下的洛伦兹破坏能标为[16]

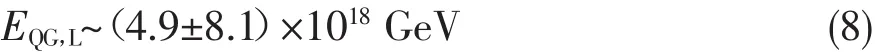
平方能量依赖情况下的洛伦兹破坏能标为[17]

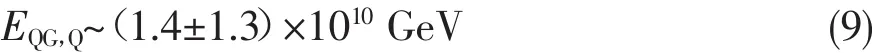
从上面两个旨果中可以看到，不同伽玛暴所预言的能量大小之间存在很大的差异[16－17]。这里，就反应出理论的不自洽性或者唯象模型中缺少着重要的因素。

在上面的讨论中，有个非常强的假设，就是这些γ－暴中的高能光子与低能光子是同时发射的。但是，这些光子是否是同时发射的呢？这还是一个非常头疼的天文问题。事实上，研究γ－暴的辐射机制的科学家们，对于γ－暴辐射的问题，还没有一个非常好的共识。另一方面，从方程(8)和方程(9)中，可以看到，使用简单的假设，也就是方程(7)，得到的结论比较分散，对中心值的集中很弱。出于以上两点考虑，有必要引入伽玛暴的天体物理源辐射机制对于高级光子与低能光子的延迟的影响。2006年，Ellis等人首先做了这方面的尝试，分析了BATSE，HETE和Swift的伽玛暴的高能延迟现象[18]。但当时的数据并没有明确的高能延迟现象的观测，所以，他们的结论给出的洛伦兹破坏的能标的可信度不高。现在，由于有了Fermi LAT的高能光子的观测，已经明确看到了高能光子相对于低能光子的延迟，那么，就有必要真正认真地考虑一下这样的观测能够给出什么样的洛伦兹破坏能标[16]。

在考虑源效应的分析中，最主要的出发点是，洛伦兹破坏下光子传播的延时是随距离面暗增大的，因为它是一种传播“引力介质”的效应；而源方面的延迟则可以近似为与距离无关的一个常数Δtin。这样，方程(7)应该修改为

经过一些简单的代数操作，可以把上式转化为［16－18］

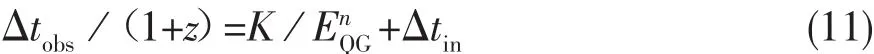
其中，

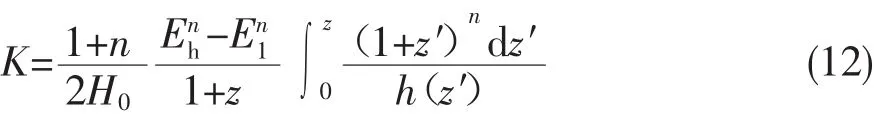
从方程(11)中可以看到，这是一个简单的直线方程，除了截距与斜率未知外，其他都是已知量；而截距代表的是源内部的效应，斜率是洛伦兹破坏能标的倒数或者数的平方。

因为源内部的延迟可能与伽玛暴的内部类型有关，从而预期长暴 (GRB 080916C，GRB 090902B，GRB 090926A)与短暴(GRB 090510)会有不同的内部延迟时间Δtin。从拟合结果可以看到[16]，长暴与短暴两种情况下，结果偏离直线的程度非常之小 (特别是只考虑长暴的情况)。具体的分析可以得到[16]，如果只考虑长暴，

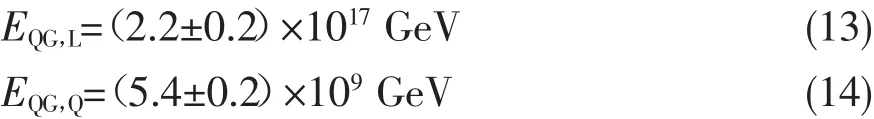
如果把短暴也考虑在内，得到的结果仍旧十分类似，而不确定性(误差)有所增大[17]，

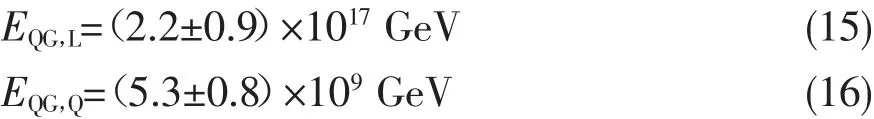
从上面的结果与前面不考虑源效应的结果对比分析可见，理论误差的减小是十分明显的。这说明了考虑源效应确实带来了一定的优越性，这样情况下的模型与真实的物理观测有更好的一致性。

3 总结

洛伦兹破坏的研究是出于对标准模型与广义相对论理论存在着严重的冲突的考虑，也是对新物理—量子能上能下力理论—的有益探索。很多的洛伦兹破坏下放都给出了修正的能动量色散关系，从而导致了丰富多彩的洛伦兹破坏唯心论像学。而到关重要的是，这些现象中有很多是可以通过地面实验或者天文观测来检验的，从而能够使得背后吏深屋次的量子引力理论受到部分的检验。这无疑是激动人心的物理探究领域。

这方面的研究是近10年内才特别地兴盛起来的，并迅速吸引了很多物理学家的极大关注。从理论方面说，这里还有很多的理论问题与检验问题需要澄清与探讨；可幸的是，从实验与观测方面来说，随着现在的实验观测技术的改进与新兴的观测平台的发展，如Fermi卫星，Pierre Auger和HESS望远镜等，洛伦兹破坏物理有望在近10年内有重大的进展，为人类进一步认识时空的基本性质做出贡献。

参孝文献

[1]Mattingly D.Modern tests of Lorentz invariance[J].Living Rev Rel，2005，8：5-84.

[2]Kostelecky V A，Samuel S.Spontaneous breaking of Lorentz symmetry in string theory[J].Phys Rev，1989，D39：683-685.

[3]Amelino-Camelia G.Potential sensitivity of gamma-ray burster observations to wave dispersion in vacuo[J].Nature，1998，393：763-765.

[4]Gambini R，Pullin J.Nonstandard optics from quantum spacetime[J].Phys Rev，1999，D59：124021.

[5]Amelino-CameliaG，Majid S.Wavesonnoncommutativespacetimeandgamma-raybursts[J].Int J ModPhys，2000，A15：4301-4324.

[6]Garroll S M.Noncommutative field theory and Lorentz violation[J].Phys Rev Lett，2001，87：141601.

[7]Lukierski J，Ruegg H，Zakrzewski W J.Classical and quantum mechanics of free κ-relativistic systems[J].Ann Phys，1995，243：90-116.

[8]Colladay D，Kostelecdy V A.CPT violation and the standard model[J].Phys Rev，1997，D55：6760-6774.

[9]Colladay D，Kostelecky V A.Lorentz-violating extension of the standard model[J].Phys Rev，1998，D58：116002.

[10]Myers R C，Pospelov M.Ultraviolet modifications of dispersion relations in effective field theory[J].Phys Lett，2003，90：211601.

[11]Shao L，Ma B-Q.Lorentz violation effects on astrophysical propagation of very high energy photons[J].Mod Phys Lett，2010，A25：3251-3266.

[12]Liberati S，Maccione L.Lorentz violation：motivation and new constraints[J].Ann Rev Nucl Part，2009，Sci59：245-267.

[13]Shao L，Ma B-Q.Lorentz violation induced vacuum birefringence and its astrophysical consequences[J].Phys Rev，2011，D83：127702.

[14]Jacob U，Piran T.Lorentz-violation-induced arrival delays of cosmological particles[J].J Cosmol Astropart Phys，2008，0801：031.

[15]Abdo A A.A limit on the variation of the speed of light arising from quantum gravity effects[J].Nature，2009，462：331-334.

[16]Shao L，Ma B-Q.Lorentz violation from cosmological objects with very high energy photon emissions[J].Astropart Phys，2010，33：312-315.

[17]Xiao Z，Ma B-Q.Constraints on Lorentz invariance violation from gamma-ray burst GRB090510[J].Phys Rev，2009，80：116005.

[18]Ellis J.Robust limits on Lorentz violation from gamma-ray bursts[J].Astropart Phys，2006，25：402-411.