混沌系统在数字图像加密中的应用研究

聂文梅，李 媚

（山西大同大学数学与计算机科学学院，山西大同037009）

20世纪下半叶,非线性科学得到了蓬勃的发展[1]。其中,对混沌理论的研究占了很大份额。混沌变换的初值敏感性、混合等基本特性与密码学有着天然的联系。例如,混沌的轨道混合特性对应了传统加密系统的扩散特性,而混沌信号的类随机性和对系统参数的敏感性对应了传统加密系统的混乱特性。他们之间这种特有的天然联系和结构上的某些相似性,使得混沌理论被广泛应用到了加密领域。当前混沌加密的方法主要包括:

(1)用密钥或明文做混沌系统的初始条件或系统结构参数,然后再通过混沌系统适当次数的迭代产生密文;

(2)利用单个或多个混沌系统来产生伪随机序列作为密钥序列,实现对原始数据的加密;第一种方式对应于分组密码而第二种方式对应于流加密。

本文考虑第二种的流密码方式。流密码系统的核心设计部件是伪随机数发生器:它决定着一个流密码系统的安全性。流密码强度依赖于PRNG所生成序列的随机性和不可预测性[2]。

伪随机序列的产生算法层出不穷,目前较流行的主要有下面几类:

(1)利用Logistic映射先产生混沌的二值序列,然后将所得二值序列进行某种函数运算从而得到最终的伪随机序列;或利用Logistic映射生成两个混沌实值序列,通过比较两个序列值的大小从而生成二值序列;或利用时空混沌系统生成实值序列,然后二进制化序列的小数部分从而生成二值序列[3];

(2)利用三维混沌系统来生成混沌序列,然后对序列进行改进进而生成所需的序列;

(3)利用超混沌系统来生成伪随机序列,超混沌系统被称作是一种特殊的混沌系统,因为其具有两个或两个以上正的Lyapunov指数。这种方法先多位量化混沌实值来生成多个二值序列,然后对其进行异或运算从而生成最终的混沌序列,这种方法可以有效避免计算机有限精度效应所引起的序列短周期问题。

前两种方法使用单一较低维的混沌系统,加密系统的安全性较低,而且其中有些序列已经成功的得到破译。采用第三种方法就目前来说是比较安全的,因为对于混沌系统来说,正的Lyapunov指数越多,表示系统轨道的不稳定的方向越多,随机性越强,因而利用该种系统所生成的伪随机序列的安全性就越强,就目前计算机的计算水平,想要破译是有一定困难的。

本文采用广义猫映射和陈氏超混沌系统相结合的方式对图像进行加解密研究。

1 混沌动力系统和超混沌序列生成

1.1 离散化处理后的广义猫映射定义[4]

离散化处理后的广义猫映射定义如下：

1.2 陈氏超混沌系统∶[5]

陈氏超混沌系统是

其中，a，b，c，d和k均为系统参数。当-0.7≤k≤0.7和a=36,b=3,c=28,d=-16时,系统进入了超混沌状态。当k=0.2时,其Lyapunov指数为λ1=1.552,λ2=0.023,λ3=0,λ4=-12.573。

1.3 超混沌序列的产生

求解混沌系统微分方程组,令步长h=0.01,首先对陈氏超混沌系统进行N次迭代以保证其进入稳定状态,接下来继续迭代超混沌系统来生成二值序列,具体方法如下:

1)首先设定系统初始值,求解系统方程组,先迭代超混沌系统N次,然后继续迭代,生成4个实数值分别为x1，x2，x3，x4,接下来通过以下式子(3)得到实数值的小数部分。

其中,Abs(x)返回x的绝对值,Floor(x)返回不大于x的整数值,t表示迭代次数。

2)用二进制来表示上一步所生成的实数值的小数部分,对于xt,如下式(4)所示:

其中,bi=1或0,n表示的是计算机精度,i=1,2,…,n-1。

3)分别取上一步所生成的二进制小数部分从而得到二值序列X={b1,b2,…,bi,…,bn-1}。

4)将得到的4个二值序列按下式(5)进行异或运算,得到一个新的序列Xt(i):

5)继续迭代超混沌系统,并重复上述4个步骤,顺次排列得到的二值序列,直至所需要的长度从而得到最终的超混沌序列L。

2 基于混沌动力系统的加密/解密算法

针对数据图像的特点,为增加图像的安全性在以下算法中仍采用位置变换和像素值改变相结合的方式对其进行加密。由于Arnold是最简单快速的一种像素置乱方法,所以进行位置变换时仍然采用广义猫映射。另外采用了陈氏超混沌系统来对像素值进行改变。

2.1 加密算法

Step1:首先读入一个数字图像文件令其为I(i,j),其中i=0,1,…,W;j=0,1… H;如果W≠H,则对边缘进行值填充,填充时,可用数值0或255,从而使W=H。

Step2:输入密钥K=(n1,n2,a,b,k,x10,x20,x30,x40),其中n1是位置置乱次数,n2是陈氏超混沌系统的初始迭代次数,a,b是Arnold映射的C的两个元素,k和x10,x20,x30,x40分别是陈氏超混沌系统的系统参数和初值。

Step3:对图像利用Arnold映射进行n1次的位置置乱。并保留其置乱后的结果I'(i,j),等待对其利用陈氏超混沌系统序列进行像素值改变。

Step4:利用前面所介绍的超混沌序列的产生方法生成超混沌序列L。

Step5:将L每八位为一组转化成无符号的整数,从而得到整数值序列Xn,利用以下式子,进行密文反馈加密,得到最终加密图像。

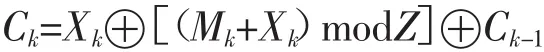
其中，Mk表示明文,Z表示图像灰度级,Ck表示密文。

Step6:判断数字图像的加密是否完成。如果完成进入下一步;否则返回Step 2再进行新一轮的加密。

Step7:加密完成,保存并输出加密结果。

2.2 解密算法

解密算法较简单,因为矩阵具有可逆性,所以对于采用Arnold映射进行位置置乱的恢复只需将伴随矩阵C用其逆阵代替即可,由于加密过程使用异或运算以及加密反馈算法,很容易从加密算法中得到解密算法,故不再赘述。

3 仿真实验结果及算法分析

3.1 仿真实验及结果分析

利用MATLAB 7.8.0软件,采用上述算法,对“penguin.jpg”图像进行了加/解密的仿真实验,密钥选取:K=(50,1000,1,2,0.2,0,0,0.0001,0),得到实验结果分别如下图1，2，3，4。

图1 原图像

图2 加密后图像

图3 解密后图像

图4 错解密图像

图2 “加密后的penguin.jpg”为图1原图像的加密结果,显然从中已经看不出原图像的任何信息,加密算法取得了较好的效果;图3解密后的图像为对图2加密后图像的解密结果,通过比较图1和图3得知,两个图像的像素值完全相同,说明采用本文提到的算法进行加密不会造成任何图像原始数据信息的丢失;图4错解密图像是将陈氏超混沌系统的初始值置为(0,0,0.000 2,0)即只改变x30值所得的解密结果,显然,只简单的修改初始值即只让x0仅仅相差0.000 1也不能正确解密,而且从解密结果图4中还可以看出得不到原图像任何信息,这一结果充分说明了算法中混沌系统的初值敏感性,也充分体现了算法的安全性。

3.2 基于混沌的算法分析

1)混乱和扩散效果分析。错误扩散是指密文的很小错误就能转变成明文很大的错误。因为对混沌系统而言,如果正的Lyapunov指数越多,表明系统轨道不稳定的方向就越多,其随机性就越强,那么基于该混沌系统生成的随机序列的安全性就越强。而且本算法在生成随机序列L时,首先采用了四个值的异或,加密时,又采用密文反馈的加密过程,这些措施都尽可能的实现了混乱与扩散,用于掩盖明文与密文间的关系,显然,如果在加密过程中某一处出错的话,错误扩散将导致整个图像不能正确的解密,进一步又增强了图像的加密效果。

2)密钥分析。初始密钥的强弱是衡量一个密码算法安全与否的重要指标。该算法的密钥K为(n1,n2,a,b,k,x10,x20,x30,x40),该算法中初值(x10,x20,x30,x40)可以取值于(0,1)之间的任何值,k可以取[-0.7,0.7]其密钥空间无穷大,n1，n2，a，b的不确定性,更极大地增大了密钥空间,从而使得对密钥K的穷举攻击变得不可行。

除了从密钥空间角度的分析,密钥是安全的,从密钥敏感依赖性而言,由于混沌系统的初值敏感性使得密文对初始密钥敏感性增强,从而进一步增强了算法的安全性。

3)算法充分考虑了位置变换和像素值改变相结合的图像加密方式,采用像素值变换可以极大地改变图像的直方图,在一定程度上抵抗统计分析攻击。本文在提出的算法中采用陈氏超混沌系统生成的序列对图像灰度置乱即像素值改变,使得原来较集中的分布在某些灰度上的像素值加密后能够均匀分布在整个灰度值空间,说明该加密方法具有很好的灰度值均匀分布的特性,另外又结合广义猫映射进行位置置乱,使得整个加密算法加密效果更好、更安全。

结束语

本文利用Arnold和陈氏超混沌系统对数字图像进行了加解密研究,通过仿真实验结果和算法分析表明,该算法具有较好的加密效果和较强的安全性.但只是简单的对算法进行了分析以及仿真实验验证,证明其加密效果良好,还有待进一步与其它加密算法作详细比较性研究,从而证明其优越性.

[1]廖晓峰,肖迪,陈勇，等.混沌密码学原理及其应用[M].北京:科学出版社,2009.

[2]宋少忠,颜辉.电子商务安全与支付[M].北京:中国水利水电出版社,2009.

[3]Li Ping,Li Zhong,Halanga W A,et al.A multiple pseudor andombit generator based on a spatio temporal chaotic map[J].Physics Letters A,2006,349(6):467-473.

[4]黎罗罗.Arnold置乱变换周期分析[J].中山大学学报,2005,44(2):124.

[5]刘金梅,丘水生,刘伟平.基于超混沌系统的图像加密算法的安全性分析[J].计算机应用研究,2010,27(3):1042-1043.