沃利斯(Wallis)公式及其应用

王振芳，陈慧琴

(山西大同大学数学与计算机科学学院，山西大同037009)

在积分学中我们经常会遇到如下的沃利斯(Wallis)公式[1-3]:

或

沃利斯(Wallis)公式揭示了π与整数之间的一种很不寻常的关系。但在实际学习中很少注意到沃利斯(Wallis)公式，更不会关注它的应用。实际上，沃利斯(Wallis)公式有许多作用，经常有以下几方面的应用。

1 应用于极限计算中

由于沃利斯(Wallis)公式与极限有关，所以有些极限的计算可以通过沃利斯(Wallis)公式很容易计算出来。

解法2 利用沃利斯(Wallis)公式(2)，可得

从上面两种解法可以看出，解法一需要构造合适的数列后，然后再用迫敛性。而解法二转化为公式形式后直接应用公式便可得，从而使得极限计算简化。

2 应用于积分计算中

对于一些用积分法不易求出原函数的积分，而利用沃利斯(Wallis)公式却很容易解决问题。

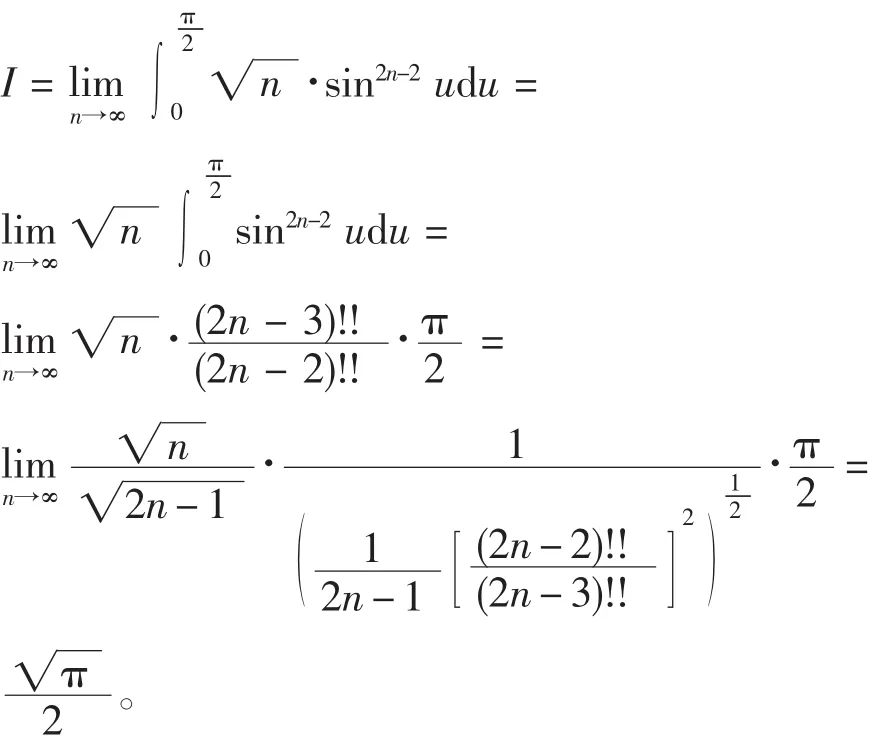
3 应用于数项级数收敛的判别

针对一些正项级数收敛性的判别，利用沃利斯(Wallis)公式会起到事半功倍的效果。

例3 判别正项级数

的敛散性。

解 由沃利斯(Wallis)公式(2)有

沃利斯(Wallis)公式除了以上的应用外，还有其他一些应用，这里不再列举说明[4－5]。但要利用沃利斯(Wallis)公式时，适用所要处理的问题中含有形如的项。如果含有这些式子，利用沃利斯(Wallis)公式，可以使得问题简化，起到很好的作用。

[1]裴礼文.数学分析中的典型问题与方法[M].北京:高等教育出版社，1993.

[2]裘兆泰，王承国，章仰文.数学分析学习指导[M].北京:科学出版社，2004.

[3]刘玉莲，杨奎元，刘伟，等.数学分析讲义学习辅导书(上册)[M].北京:高等教育出版社，1987.

[4]陈慧琴，李秀兰.论积分的可减性[J].山西大同大学学报:自然科学版，2009，25(5):10－12.

[5]唐雄，陈莹.计算含参量反常积分的一些特殊方法[J].山西大同大学学报:自然科学版，2008，24(2):8－10.