绿波协调控制系统运行状态的动态监控方法*
郭海锋
(浙江工业大学信息工程学院 杭州 310023)
所谓“绿波”,是指车流沿某条主要路线行进过程中,连续得到一个接一个的绿灯放行信号,畅通无阻地通过沿途所有交叉口.已有的绿波协调控制方法,从不同角度选择优化目标,寻求单向或双向绿波协调控制系统的最优带宽[1-3].虽然已相对成熟的城市道路交通状态判别方法可以判别道路交通状态,但是方法中需要的交通数据在现实状况下还很难获得[4-5].此外,对于干线协调控制系统而言,某一路段或某一交叉口发生拥挤,未必会立即导致干线协调控制失效,若以此为依据切换信号控制方案可能会使控制效果不理想.本文以道路上交通检测器采集到的实时交通数据为基础,设计一种有效协调时间的计算方法,监控绿波协调系统的运行状态,并以VISSIM为工具通过编程对上述方法进行模拟验证.
1 有效协调时间
由图1、图2可以看出,设计带宽是一个理论值,适合低流量情况.在高流量及饱和情况下,实际运行中各交叉口绿灯前段时间通常先放行停车线前的排队车辆,绿灯后段时间才参与绿波协调放行上游驶来的车流.如果交叉口绿波方向排队车辆数较多,将导致该交叉口参与绿波协调的时间较少,即占用了设计带宽的一部分时间用于放行绿灯起始时刻停车线前的排队车辆.由此可见,各交叉口有效协调时间越小,意味着从上游驶出的车流能连续通过下游交叉口的概率越小,当有效协调时间低于某一阈值时,绿波协调将难以实现,因此,有必要实时计算有效协调时间的数值.
在本文研究中,有效协调时间(available coordinated time,ACT)是指绿波协调控制过程中能够真正起到绿波通行作用的那部分时间.

图1 理想情况下绿波协调控制系统时-空图

图2 拥堵情况下绿波协调控制系统时-空图
由图1、图2及前述分析可知,某一个相位的绿灯时间可分为两部分,一部分用于释放停车线前的排队车辆,另一部分释放上游交叉口当前绿灯放行过来的车辆,使其无阻滞地通过交叉口.本文将前者记为本地时间Gloc(i),将后者记为弹性时间Grem(i).
在某一信号周期内,各交叉口绿波方向的弹性时间Grem(i)越多,系统获得的有效协调时间越多.整个系统的有效协调时间受各交叉口中最小的弹性时间制约,即某个交叉口的弹性时间Grem(i)较小,则会影响当前信号周期整个系统运行的有效协调时间,成为系统的瓶颈点.
2 计算方法
本文以SCATS系统为例,该系统每组最多支持6个交叉口进行绿波协调控制,因此设计有效协调时间计算方法时假定参与绿波协调的交叉口数量为N,2≤N≤6;同时假定绿波方向参与协调的末端交叉口与其下游相邻交叉口间的路段较长,足以容纳末端交叉口释放的车辆而不会排队溢出.
2.1 Gloc和Grem的计算
SCATS系统停车线前各车道布设有检测器,能够实时计算出相邻两辆车通过检测器的时间间隔.饱和情况下,绿灯开始的前期阶段,排队车辆以车队的形式通过检测器,饱和车头时距通常为1.5~3.5s[6].
本文对某一实际路口进行了实际调查,绿灯期间通过的车辆均是小车,车头时距见图3所示.经过数据统计分析,排在队前的车辆车头时距较大,排在队尾的车辆车头时距较小,最小的车头时距为1s,15辆车放行完毕后,逝去的绿灯时间为29s,该方向绿灯时间为35s,因此绿灯剩余时间为6s.
由此可知,若检测器检测到的车辆间隔时间大于饱和车头时距,则可认为排队车辆已放行完毕,绿灯剩余时间为弹性时间,可用于放行上游正驶来的车辆.

图3 饱和车头时距分布图
设相邻车辆通过检测器的间隔时间为Tgap,某交叉口绿波方向所在相位绿灯时间为G(i),则
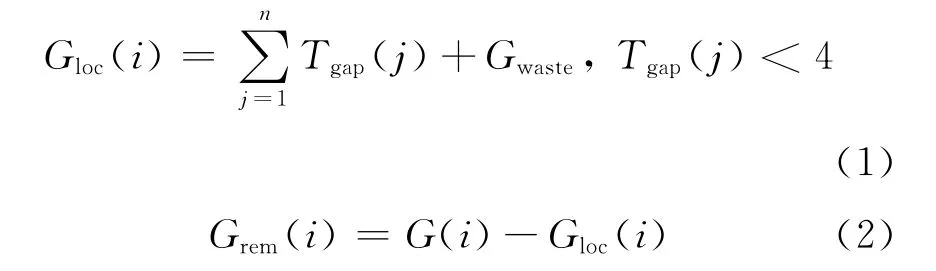
式中:Tgap(j)为检测到的第j个间隔时间,当Tgap(j)小于4s时,认为释放的是排队车辆;一旦Tgap(j)大于4s,则后续再检测到的车辆认为是上游交叉口刚放行驶来的车辆,间隔时间不再参与公式(1)的计算,Gwaste为绿灯初始损失时间.
显然,0≤Grem(i)≤G(i),即若绿灯起始时刻,停车线前排队车辆数为0,则当前交叉口的绿灯时间可全部用于绿波协调;若当前交叉口绿灯起始时刻停车线前排队车辆数较多,则Grem(i)将趋于0,即交叉口用于绿波协调的时间为0.
2.2 有效协调时间的计算
由前述分析可知,绿波协调控制系统当前信号周期的有效协调时间计算见式(3),即当前系统最小的Grem(i)值.

有效协调时间的计算过程如下:(1)监测交叉口i绿波方向红灯时间是否结束,如果是则转向(2),否则继续监测,i=1,2,…,N;(2)获得当前信号周期交叉口i绿波方向的绿灯时间 ,i=1,2,…,N;(3)计算交叉口i的本地时间Gloc(i),i=1,2,……,N;(4)计算交叉口i的剩余时间Grem(i),i=1,2,……,N;(5)计算 N 个交叉口的最小剩余时间 min{Grem(i)},即有效协调时间ACT;(6)输出当前信号周期绿波协调控制系统的有效协调时间,并对 min{Grem(i)}所属的交叉口i给予1分惩罚,即punish(i)=punish(i)+1;(7)如果ACT小于阈值d,则当前绿波协调控制失效,输出 max{punish(i),i=1,...,N}所属的交叉口Int(i);否则转步骤(1),对下一信号周期进行监测.
2.3 瓶颈交叉口的确定方法
本文以当前绿波协调控制系统的信号周期为时间间隔,在每个信号周期结束时,选取Grem(i)最小的交叉口,并给予其数值为1分的惩罚.当绿波协调控制系统的有效协调时间低于某一阈值时,则表明当前的绿波协调控制失效,此时获得惩罚分数最大的交叉口即为该系统的瓶颈交叉口.确定瓶颈交叉口的流程图见图4所示.

图4 确定绿波协调控制系统瓶颈交叉口流程图
由木桶理论可知,实际运行中绿波协调控制系统的有效协调时间受系统中瓶颈交叉口的影响较大,系统实际执行的有效协调时间取决于该瓶颈交叉口所能获得的绿灯剩余时间.
3 模拟实验
3.1 方案设计
图5所示,以连续的五个交叉口为研究对象,5个交叉口所在的道路为城市主干路,各交叉口间距离约为600m.在实验中以VISSIM模拟软件为工具,利用VB调用VISSIM的COM接口,读取检测器数据及信号控制机参数,模拟时间为3 600s,设置的交通流量随仿真时间的增加而逐渐增大.
各交叉口东西方向进行绿波协调控制,共用信号周期时长为100s,系统设计的带宽为25s,即理论上在带宽所辖25s时间范围内,自交叉口E驶出的车辆能够无阻滞地顺利通过交叉口A.
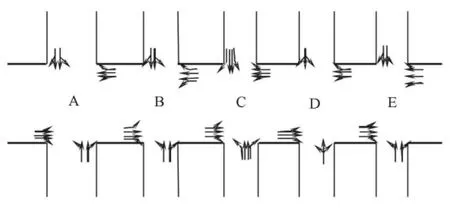
图5 交叉口的渠化结构示意图
3.2 绿波协调控制系统的运行状态
图6中,横轴为绿波协调控制系统的共用信号周期,纵轴为每一信号周期干线系统的有效协调时间.从图6中可见,模拟期间绿波协调控制系统的有效协调时间随着交通流量的增大而逐渐减小.因此,可以通过监测有效协调时间的动态变化对绿波协调控制系统的运行状态进行动态监控.
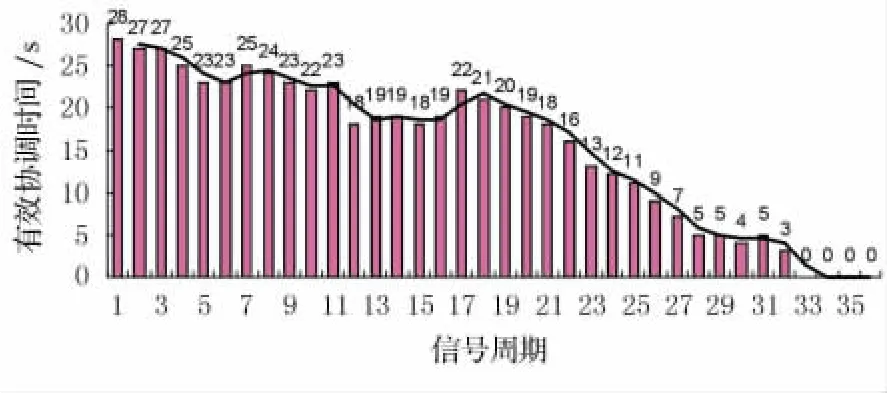
图6 绿波协调控制系统有效协调时间
模拟结果表明,拥堵状况下绿波协调控制既不能实现理论上的“绿波”通行,又不能对拥挤的车流给予及时疏导.因此,出现拥堵时应及时切换信号控制方案.
3.3 有效协调时间阈值分析
有效协调时间阈值d的确定直接影响干线不同信号控制方案的切换时机.为了确定最优d值,本文采用试探的方法对d分别取值为3,4,5,6,7,当有效协调时间小于d时,则将信号控制方案切换为已有文献所采用的TSS-CAI控制方案[7],并对不同取值的实验结果进行了对比分析,见表1所列.
实验表明,当d=5时,模拟期间系统的性能指标最优,即当有效协调时间小于等于5s时已有的绿波协调控制系统应该切断绿波,而改用其他有利于疏导拥挤交通流的信号控制方案,以便及时地对拥挤的车流进行疏导.
4 结 论
1)绿波协调控制系统实际运行的效果取决于系统各信号周期能够获得的有效协调时间,高峰及拥堵情况下有效协调时间较小,因此个别信号周期会出现路段排队车辆溢出至上游交叉口的现象.
2)确定的瓶颈交叉口,有利于对拥堵的成因进行深入分析,进一步提高干线系统的通行能力.
3)仿真实验结果表明,利用有效协调时间计算方法,能够对绿波协调控制系统的运行状态进行实时监控,为确定不同干线交通信号控制方式的切换时点提供技术支持.

表1 不同有效协调时间阈值d的对比分析结果
[1]马 楠,邵春福,赵 熠.基于双向绿波带宽最大化的交叉口信号协调控制优化[J].吉林大学学报:工学版,2009,39(S2):19-24.
[2]吴 震.基于仿真的干线协调控制分析指标[J].武汉理工大学学报:交通科学与工程版,2010,33(2):349-352.
[3]Gartner N H,Stamatiadis C.Arterial-based control of traffic flow in urban grid networds[J].Mathemat-ical and Computer Modelling,2002,35(5-6):657-671.
[4]邹 亮,徐建闽,朱玲湘.基于融合技术的道路交通状态判别模型[J].清华大学学报:自然科学版,2007,47(2):1 822-1 825.
[5]姜桂艳,郭海锋,吴超腾.基于感应线圈数据的城市道路交通状态判别方法研究[J].吉林大学学报:工学版,2008,38(S1):37-42.
[6]赵 星,任 刚.信号交叉口车头时距特性分析[J].交通运输工程与信息学报,2010,8(1):103-109.
[7]郭海锋.局部拥挤条件下城市道路交通信号控制方法研究[D].长春:吉林大学交通学院,2008.

