基于Matlab的飞行模拟器电动加载系统控制仿真研究*
刘长华 宋 华
(中国民航飞行学院飞行技术与飞行安全科研基地1) 广汉 618307)
(北京航空航天大学自动化科学与电气工程学院2) 北京 100191)
式中:ην,ηw 为学习步长.
电动加载系统是飞行模拟器的重要组成部分,它模拟飞机驾驶杆力,为飞行员的训练提供近似真实的飞行环境[1].在真实的环境中,飞机驾驶杆力受到连杆、齿轮间隙和电机自身存在的多余惯性力矩等多种非线性干扰的影响,使电动加载系统的模型在很大的范围内变化.为了保证控制效果,需要对人感系统选取合理的控制器.本文基于PIDNN(proportional integral differential neural network)对飞行模拟器电动加载系统模型进行仿真控制.PIDNN作为智能控制的一个分支,简单规范、学习速度快,能有效对模拟器电动加载系统进行实时控制[2].
1 模拟器电动加载系统控制模型
1.1 系统原理与模型
飞行模拟器驾驶杆力的大小不仅与杆的位移有关,还与杆的运动状态(速度和加速度)有关,杆力近似公式为

式中:F为握杆点力;x为杆顶端位移;Kα,Kβ分别为位移、速度到操纵杆力的转换系数,可由理想杆力公式和系统传函比较求得;P为其他因素产生的力(理想运算可忽略).
电动加载系统由滚珠丝杠、力矩加载电机、传感器和控制器等组成,各部分模型如下.
1)操纵杆

式中:i为操纵杆的传动比;Ft为缓冲弹簧的输出力.
2)直流力矩电机

式中:Tm为时间常数,s;ωm为电机转速;Mc为电机负载;ui为电机输入电压信号;K1为电压/转速转换系数;K2为负载/转速转换系数.
3)滚珠丝杠

式中:n滚珠丝杠导程.
4)缓冲弹簧

式中:Ks为弹簧刚度;xl为转轴连杆顶端位移;Td为加在力矩电机输出上的干扰.
5)力传感器

式中:Kf为传感器力/电压转换系数.6)取前馈控制律

式中:ua=KaF,Ka为杆力/电压转换系数;ue为误差控制量.
由以上各模型综合可得电动加载系统结构示意图,如图1所示.

图1 飞行模拟器电动加载系统结构示意图
1.2 控制器传递函数
以上模型和结构示意图传递函数为

式中:H1=KσK1K2n(Kα+Kβs);H2= (Tm+1)iKsnT;H3=iK2Ksn+iKsKfK1n.
传递函数的框图如图2所示.
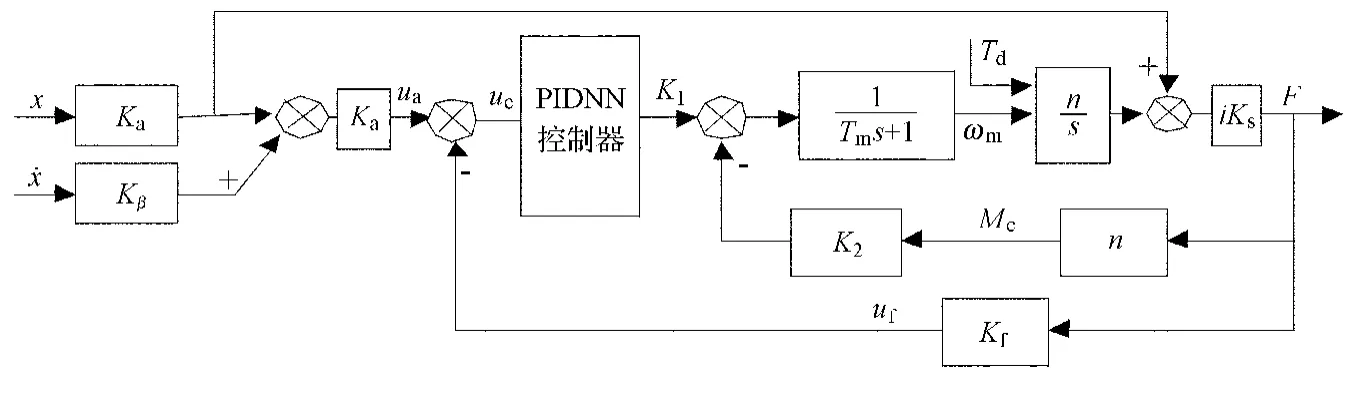
图2 飞行模拟器电动加载系统传递函数框图
电动加载系统模型已经建立,需要选择合适的控制策略,PIDNN将神经元网络和传统的PID相结合,既继承了神经元网络优良的自适应性,又发挥了PID的简洁与鲁棒性[3],所以可采用PIDNN对电动加载系统进行控制.
2 PIDNN控制器
2.1 PIDNN的结构
PIDNN是节点结构为2-3-1的3层前向反馈神经网络[4],见图3所示.
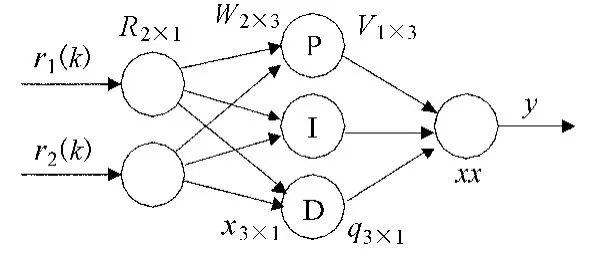
图3 PIDNN结构示意图
输入层神经元的输入为

式中:k=1,2,3,….
输入层神经元输出与输入相等.
隐层神经元的输入为

式中:x=[x1(k),x2(k),x3(k)]T隐层输入向量;W2×3为输入层到隐层的权值矩阵;wij为输入层第j个节点至隐层第i个节点的权值.
隐层比例、积分、微分神经元的输出qi(k)(i=1,2,3)的计算如下.

式中:V1×3为隐层到输出层的权值矩阵;vi为隐层第i个节点到输出层的权值.
输出层神经元输出,即网络的输出为
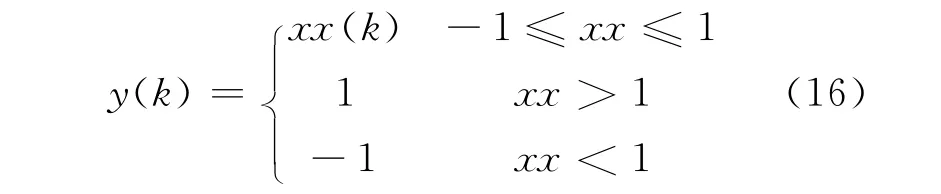
2.2 PIDNN控制器
图4所示为由PIDNN构成电动加载系统控制器的结构框图,为使输出能够跟踪输入的变化,选择经过归一化的PID神经元输入向量为
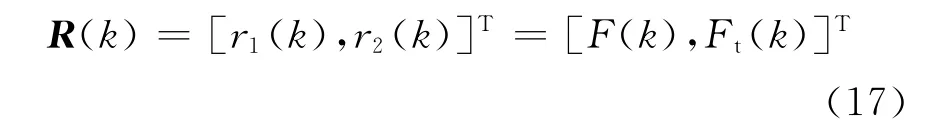
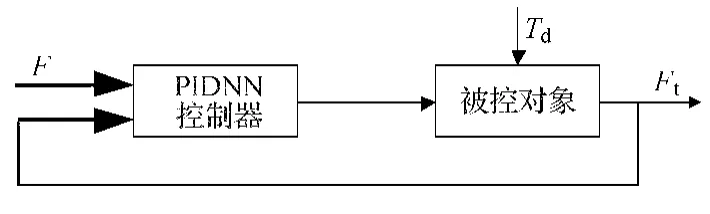
图4 PIDNN控制系统的结构
误差定义为

式中:E(k)为控制力与电动加载系统输出力的差值.
目标函数定义为

根据B-P算法[5],经过k步训练后,隐层至输出层权值在线调整算法为
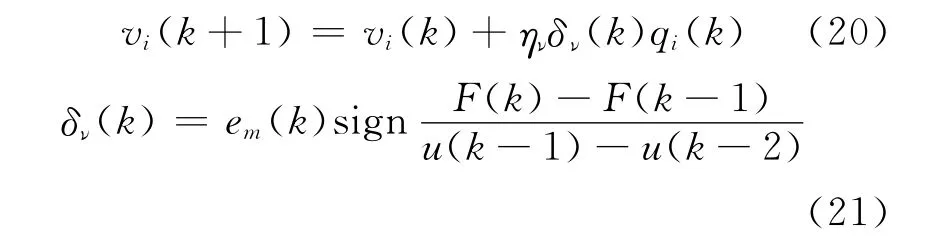
输入层至隐层权值在线调整算法

式中:ην,ηw为学习步长.
3 Matlab仿真
为了验证系统的稳定性,采用阶跃输入加阶跃干扰的方式在Matlab环境下进行仿真.
驾驶员在俯仰通道施加的力为0~20N[6],所以仿真试验选取|F|=20N.
如果用PID进行控制,需要对P,I,D的参数进行筛选,这是一件很繁琐的事情.并且由于PID控制器不能进行自适应,3个参数未选好时控制效果不是特别理想,如图5所示.下面用PIDNN进行仿真控制.

图5 PID控制器未选好参数的仿真波形
选取W和V的初始值为

学习步长定为

如图6所示为不加任何干扰的情况下PIDNN控制电动加载系统输出Ft跟踪控制输入F=20N(阶跃信号)的曲线.仿真到最后参数自动调整为

可见PIDNN能快速调整自身参数,控制电动加载系统输出迅速跟踪输入,无超调,稳态误差为0.

图6 无干扰时PIDNN控制电动加载系统跟踪曲线
图7所示为F=20N,1s时Td=10N的情况下,PIDNN控制电动加载系统输出Ft跟踪控制输入F=20N(阶跃信号)的曲线.仿真到最后参数自动调整为

可见PIDNN神经网络亦能很快调节自身参数,使系统对干扰的抵抗能力加强,调节时间短,稳定性高,鲁棒性很好.

图7 有阶跃干扰时PIDNN控制电动加载系统跟踪曲线图
4 结束语
从结果中可以看出,PIDNN控制器结构简单,具有很好的鲁棒能力和适应性,能很快调整参数,保证控制精度,可对飞行模拟器电动加载系统模型进行优化控制.
[1]沈东凯,华 清,王占林.基于神经网络的电动加载系统[J].航空学报,2002,23(6):255-259.
[2]董伟杰,刘长华,宋 华.基于PIDNN控制的飞行模拟器人感系统[J].北京航空航天大学学报,2008,34(2):153-157.
[3]徐丽娜.神经网络控制[M].北京:电子工业出版社,2003.
[4]Hess R A.Analyzing manipulator and feel system effects in aircraft flight control[J].IEEE Transactions on Systems,Man,and Cybernetic,1990,20(4):923-931.
[5]Shu Huailin,Pi Youguo.PID neural networks for time-delay systems[J].Computer and Chemical Engineering,2000,24(7):859-862.
[6]董新民,王小平.飞行模拟器电动式纵向操纵人感系统的研究[C]//中国航空学会第八次飞行器控制与操纵学术交流会论文集.湖北,襄樊:中国航空学会,1999:92-96.

