远场弱磁信号的小波域自适应检测研究

张 宁 庞学亮 林春生 于李洋

（海军工程大学兵器工程系1） 武汉 430033） （海军驻大连426厂军事代表室2） 大连 116005）

0 引 言

水中磁性运动目标，如钢壳舰船、潜艇等，是水中兵器的探测目标，磁探测系统在接收到目标的磁场信号并判断为打击对象、且在打击范围时，控制武器攻击目标并击毁目标，因此，对磁性运动目标的可靠探测，是水中兵器系统的关键技术问题之一.

利用目标磁场信号的波形特征，如磁场信号幅值、波形宽度和斜率等，进行目标的判断与识别，或采用频域滤波等信号预处理技术来提高引信的抗干扰能力，但这仍未能充分利用目标磁场的信息，只是利用了目标信号在时域和频域上的一些信号特征［1］.当目标很近、信号很强时，可以用简单的计算实现对目标的检测.当距离加大时，目标信号减弱，如传统的小波阈值消噪，很难消除磁暴、地磁脉动等频率范围很宽、完全覆盖了目标磁场信号的频率范围的自然干扰信号.若要系统可靠检测目标，必须提高检测灵敏度，降低检测门限，当门限低到自然干扰经常可以达到的程度时，如变化率在0.1nT／s以下，或磁场值在1nT以下，检测将有很大的虚警概率.

本文结合实测数据，采用在不同的小波分解层，选取与尺度相关的ARMA模型自适应阈值算法改进小波阈值消噪的算法，充分利用了信号的时间、频率信息，对复杂环境下舰船磁场弱信号检测与提取技术进行了研究.

1 小波域Mallat分解算法

Mallat分解算法是一种基于多分辨率分析的快速小波变换算法.其原理是利用正交小波基将信号分解为不同尺度下的各个分量.每一次分解产生高频细节分量dj（k）和低频逼近分量cj（k）两部分.由于信号的细节信息和噪声信息都包含在dj（k）中，故下一次只要对cj（k）进行分解.其变换过程相当于重复使用一组高通和低通滤波器对时间序列信号进行逐步分解.

首先选择与信号最相近的小波基函数，然后确定小波分解层次J，对信号进行J层分解，分别得到不同分解尺度的逼近和细节系数.信号的分层不是任意的，长度为N的信号分层，J≤lb N，J为自然数［2］.多分辨率分解公式如下.

式中：h0（n）＝〈φj，0（k），φj－1，n（k）〉相当于一个低通滤波器组，分解出逼近系数cj（k）；h1（n）＝〈φj，0（k），φj－1，n（k）〉相当于高通滤波器组，分解得到细节系数dj（k）；φ和φ分别为对应的尺度函数和小波基函数.常用的正交小波基有Harr小波、Littlewood－Paley小波、Meyer小波等.

信号z（t）经过小波变换处理后，可重构得到有用信号

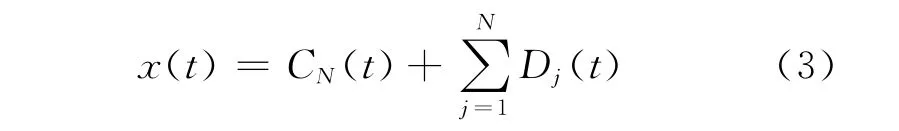
式中：CN（t）为由第N 层的逼近系数重构信息；Dj（t）为由不同尺度的近似细节系数重构信息.

2 阈值的选取

2.1 Donoho阈值提取法

目前应用最为广泛的是Donoho阈值计算方法.Donoho硬阈值法存在突变性，软阈值处理是经过比较后，将大于阈值的点变为该点与阈值的差值，通过阈值方程对二进小波变换系数WTm，n进行压缩，获得阈值消噪后的小波系数.Donoho从理论上给出并证明了在均方误差极小－极大意义下的阈值为

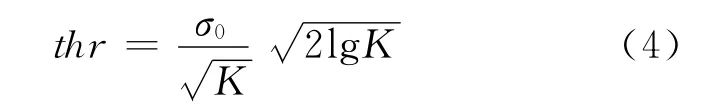
式中：K为不同尺度的信号长度；σ0为信号的标准方差.

Donoho阈值法的缺点在于，它用固定阈值处理小波系数，这样就会歪曲原始信号包含的弱特征成分，从而引起重构信号的失真.其改进软阈值消噪方法虽然考虑了阈值与尺度的关系，但没有充分考虑到噪声的统计特性与尺度的关系.在信号处理中，信号中包含的很多弱特征成分都是重要的信息成分.如果在消噪时不加区别地去除，那么重构信号就无法准确体现信号的特征［3－4］.

2.2 小波阈值的ARMA模型自适应算法

ARMA模型噪声是一类典型平稳噪声，任何具有有理谱的平稳噪声都是ARMA型噪声.另一方面，相对于平稳背景来说，动态信号是一个持续时间较短的信号，因此背景干扰ARMA模型的假设具有普遍性［5］.ARMA模型噪声

式中：U（z）是背景干扰u（n）的Z变换；E（z）是模型残差e（n）的Z变换.

为了使滤波器能适应背景干扰的缓慢变化，使用块处理自适应技术，所需滤波器的权系数正好是背景噪声的ARMR模型系数，求解这一组系数时，必需确保输入数据中没有动态目标信号出现，否则，得到的滤波器对动态目标信号也衰减很明显.为此，利用动态目标信号持续时间较短的特点，把观察时间划分为n个区间.滤波算法按下面过程进行，第一区间：假设没有动态目标信号，输入为纯背景u（n），利用这一区间内u（n）数据求解ARMA模型系数（A，B）.

第二区间 （1）用上一区间所求模型系数按式（5）构造滤波器，过滤本区间信号；（2）判断有无动态目标信号，若没有，则用该区间新求解的模型系数代替原来求解的模型系数（A，B）.

第n区间 （1）使用最近一个没有动态目标信号出现的区间所求模型系数按式（3）构造滤波器，过滤本区间信号；（2）判断有无动态目标信号，若没有，则用该区间新求解的模型系数代替原来求解的模型系数（A，B）.

滤波器的系统函数如下.

式中：a0＝1.该滤波器为ARMA模型噪声的白化滤波器.则

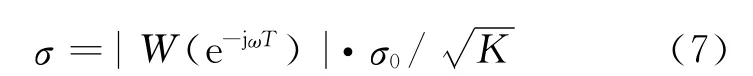
基于信号观察区间局部特征的自适应阈值设计方法［6］：根据信号局部特征，选择相应的最佳小波，在每一小波分析段，采用相应的阈值算法，即在不同小波函数段，选择不同的阈值，并且在不同的分解层，采用与尺度相关的阈值.具体阈值设计步骤如下.

1）在每个信号区间，分别计算初始阈值

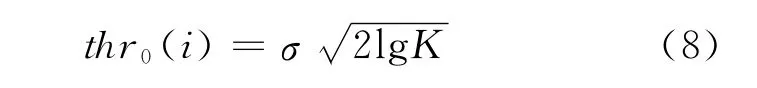
2）第j级阈值

式中：a＜1为整因子；j为小波分解的级数.

3 实测数据的算法仿真及分析

实验数据于2006年6月在浙江舟山某码头测得，实验船离岸正横距300m，系统低通截止频率0.5Hz，采样频率10Hz.船纵向棱形系数0.624，水线长126m，排水量3 150m3，航速14 kn（6.93m／s）通过测量区.

3.1 实验数据及频谱分析

图1为含目标信号的磁场信号时域图，峰峰值估算信噪比SNR＝1.58dB，目标信号（46～74 s时段）已被完全掩盖在背景场中.

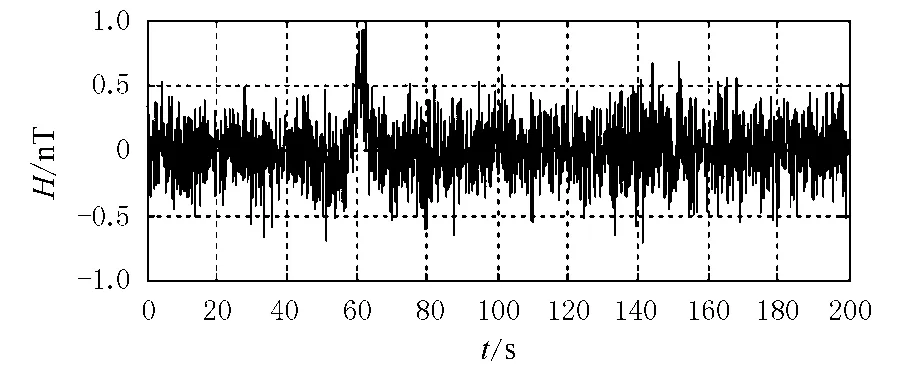
图1 实验船磁场时域信号

图2为基于Meyer小波基函数对实测信号进行5层的多尺度分析，得到的1～5层的细节信号.从图中可见，第1层细节信号的幅值较小，第2、3层细节信号的幅值有所增加，而第5层细节信号不但幅值增加，其包络曲线构成的低频成分和舰船磁场信号已非常相似.

图2 水压场信号5层Meyer小波分析

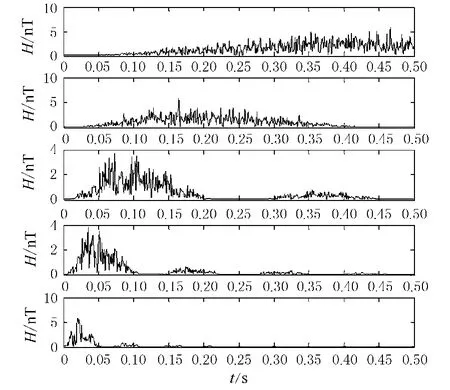
图3 各层小波的功率谱分析

分别计算各层小波的功率谱，如图3.第3，4层分解出的信号功率谱值较大，集中在0.04～0.2Hz的频带，主要成分是背景极低频磁干扰谱；第5层信号谱集中在0.03Hz左右，清晰可见舰船信号包络（参照图2）.小波变换大大的提高了在0.5Hz以下低频段的频率分辨率，且很好的将中心频率各异的舰船信号和背景信号分开来，但在0.05Hz左右的位置信号叠加严重，普通的频域滤波很难高品质的滤除干扰信号，必须选取合适的阈值进行滤波，才可以滤除幅值较大的背景噪声，提取舰船弱信号.

3.2 基于自适应阈值的小波消噪

图4上图为基于Donoho软阈值小波消噪效果.分析可见，Donoho阈值算法在滤除高频干扰成分的同时，也滤除了部分目标信号的高频分量，是滤波后的信号失真较严重.采用折中的方法，适当多保留一个邻层的细节系数，效果有所好转，不解决根本问题.

图4 自适应阈值的消噪后信号

图4下图是采用ARMA模型自适应阈值的小波消噪后的信号（a＝0.5）.输出信噪比SNR＝24.3dB，信噪比提高22.72dB.从信号处理的效果看，采用自适应滤波阈值消噪可以显著提高信号的信噪比，更好的保留目标弱信号的细节特征，对背景干扰抑制的效果更好.

针对不同环境的信号，式（9）中选取不同的a值，得到更好的提取效果.综合比较，采用自适应ARMA模型阈值的小波消噪对复杂环境下舰船磁场弱信号有很好的检测和提取能力.

4 结 论

结合小波消噪理论和自适应原理的特点，针对从强噪声信号中对微弱的舰船磁场信号进行提取的应用要求，提出了一种基于ARMA模型自适应阈值消噪的小波消噪算法.仿真结果表明，该算法在信号细节系数中进行自适应滤波，可以大大提高磁场弱信号检测的能力，是强噪声干扰背景下的弱信号检测的一种有效方法.

［1］林春生，龚沈光.舰船物理场［M］.北京：兵器工业出版社，2007.

［2］吴正国，夏 立，尹为民.现代信号处理［M］.武汉：武汉大学出版社，2003.

［3］刘 斌，张斌珍.微弱信号检测技术［M］.北京：电子工业出版社，2005.

［4］Yasotharan A，Thayaparan T.Time－frequency method for detecting an accelerating target in sea clutter［J］.IEEE Transction on Aerospace and E－lectronic Systems，2006，26（10）：1 289－1 310.

［5］林春生.平稳噪声背景下短时动态信号的自适应滤波［J］.武汉理工大学学报：交通科学与工程版，2004，28（4）：479－481.

［6］Cioffi J M，Thomas K F，Recursive－least－squares transversal filters for adaptive filtering［J］.IEEE Trans On ASSP，1984，32（2）：304－337.