椭圆方程有限差分逼近的混合半迭代法*
刘 扬 高 飞
(武汉理工大学理学院 武汉 430070)
0 引 言
现代科学技术工程中的大量数学模型都可以用微分方程来描述,求解微分方程的数值方法主要有:有限差分方法、有限元法以及有限体积法等.用有限差分法求解椭圆型方程,其差分格式的求解都归结为一个线性代数方程组问题,原则上,数值代数中的方法都适用于求解这类代数方程组.但有限差分法所得到的差分格式的系数矩阵具有一些特殊的性质,如稀疏带状、主对角优势以及不可约性.因此针对这些特点,建立了更加有效的方法,如交替方向迭代法[1]、预处理共轭梯度法[2]以及多重网格法[3]等,这些方法都是迭代法.迭代法具有程序设计简单,适合自动计算,同时还可以充分利用系数矩阵的稀疏性减少内存存贮.因此,迭代法已经成为求解线性方程组,尤其是求解具有大型稀疏系数矩阵的线性方程组的重要方法之一.半迭代法也称Chebyshev多项式加速方法,是求解线性方程组的一个常用且比较有效的方法,它是迭代法的一种.与一般迭代法相比,半迭代法不仅可以提高求解线性方程组的收敛速度,而且可以使一些发散的迭代法收敛.关于半 迭 代 法,许 多 学 者 都 对 此 作 了 研 究[4-8].Young在文献[1]中,给出了线性方程组的迭代矩阵为对称阵时,半迭代法的收敛性分析.本文利用局部消元法建立求解椭圆方程的十三点差分格式,将Chebyshev多项式加速方法应用于新差分格式,构造了一个混合半迭代法,用数值实验验证新算法的有效性.
1 局部消元法
考虑椭圆型方程第一边值问题



式中:ui,j为式(1)的解u(x,y)在网格点(xi,yj)上的近似解,λ=4+ah2,fi,j=f(xi,yj).
在Ωh的每一个网格内点(i,j)处都有一个联系于式(2)的几何Stencil.在网格点(i-1,j),(i+1,j),(i,j-1),(i,j+1)处,有另外4个差分方程

同样的方法,消去上式中的ui-1,j-1,ui-1,j+1,ui+1,j-1,ui+1,j+1,可以得到一个更复杂的差分演化格式

到这里,停止消元过程.式(4)所对应的几何Stencil如图1所示,它示出一个十三点差分格式,其局部截断误差与五点中心差分格式一样为O(h2).

图1 13点差分格式的Stencil
2 混合多项式加速算法
定义Ωh中网格点的集合Lp,称为网格Ωh的层,p是层的标号,
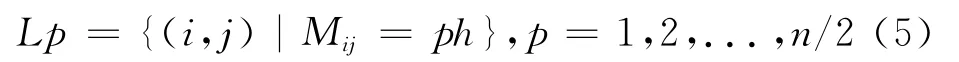
式中:Mij为网格点(i,j)到边界∂Ω的最短欧氏距离.显然,对于Lp(p=2,3,...,n/2)中任意一点(i,j)都存在一个形如式(4)的差分演化形式,根据式(2)和式(4),可以构造一个Jacobi型迭代算法(JIA算法)如下.
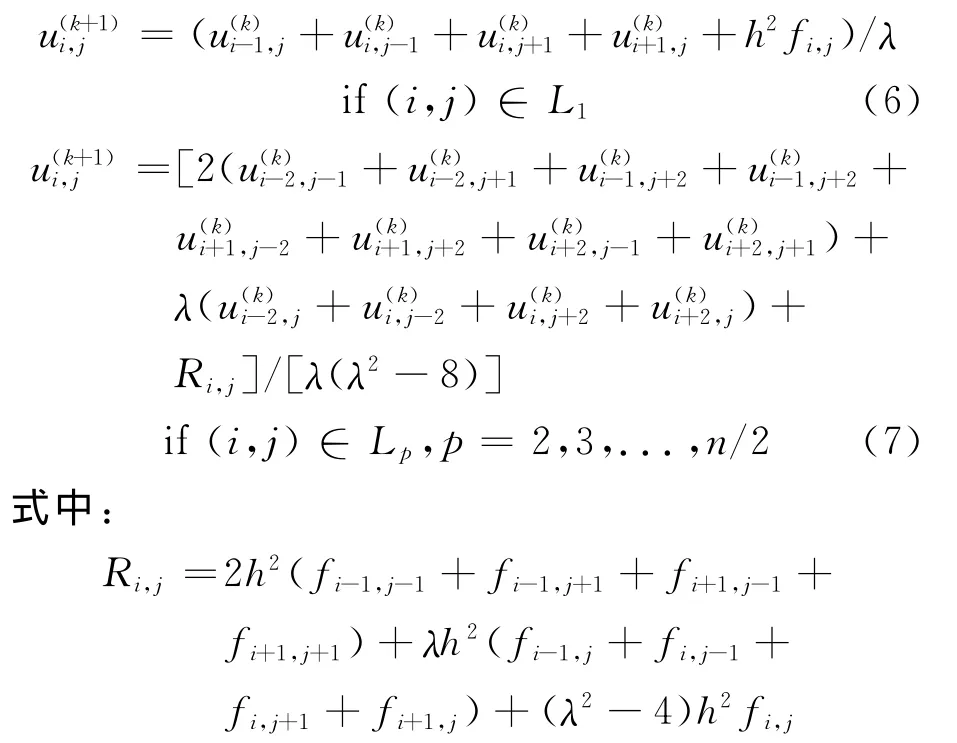
注意到上面算法中在第一层和其他层使用不同的迭代格式.对于任意给定的初始值,Jacobi型算法式(6)和式(7)是收敛的,即当k→∞时.

利用边界条件,计算|ξ(k)i,j|在每一层上可以得到的估计式,有

设内点的总层数为r,则r=n/2,由此得在所有的内点上都有

上式右端项当N→∞时趋于零,故算法收敛性得证.
将式(7)写成矩阵形式

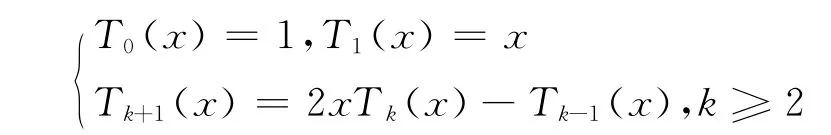
由于JIA算法中第一层上的迭代公式与内层不一致,因此根据Chebyshev多项式加速法构造一个混合半迭代法如下.
步骤1 输入变量ε(误差)的值;令k:=1.
步骤3 计算
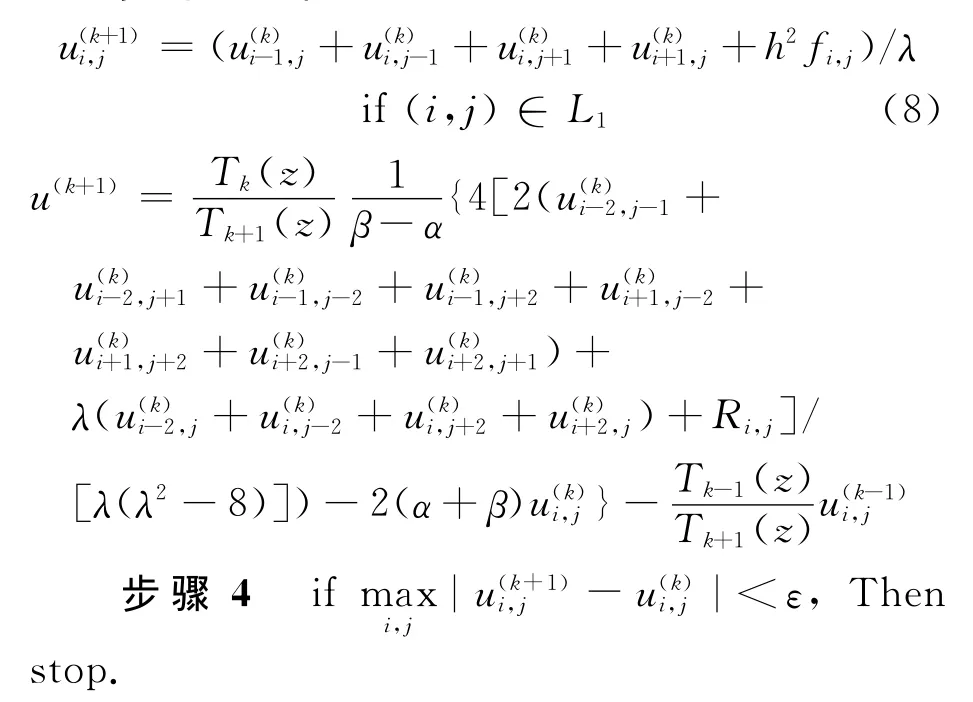
Else k:=k+1;goto步骤3.
注意到新算法中,第一层网格点的计算仍使用经典的Jacobi迭代,而内层网格点的计算使用多项式加速技术.之所以在第一层和内层网格点上使用不同的迭代格式,主要原因有两点:第一JIA算法中第一层和内层使用了不同的迭代格式;第二在实际的数值计算中,外层的误差比内层收敛快.由于JIA算法的系数矩阵是对称的,因此本文构造的混合迭代算法是收敛的.
3 数值实验
为了验证新迭代算法的有效性,考虑一个模型方程如下

式(10)的解为

取步长h=1/100,比较Jacobi方法、JIA算法、Jacobi半迭代法、混合半迭代法在所有内点上达到相同误差精度所需要的时间,结果见表1.
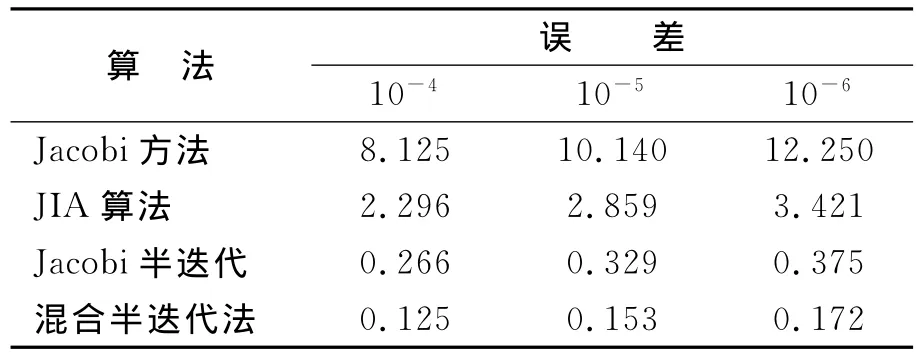
表1 迭代时间比较 s
所有结果在IBM电脑,CPU频率为1.6G的计算机上计算得到.数据结果表明:Chebyshev多项式加速方法能有效的加快迭代法的收敛速度,同时本文构造的混合半迭代法的收敛速度比Jacobi半迭代法约快一倍.
4 结 论
本文利用局部消元法构造了求解一类椭圆型方程的十三点差分格式,并结合五点差分格式建立了一个Jacobi型迭代算法.然后根据Chebyshev多项式加速方法构造了一个混合半迭代算法.新算法在第一层上仍然使用经典的Jacobi迭代,而在内层上使用多项式加速方法.数值实验表明,新算法比Jacobi半迭代法收敛快.本文的算法和思想也可用于求解其他类型的偏微分方程.
[1]Young D M.Iterative solution of large linear system[M].New York:Academic Press.,1971.
[2]Young D M.Iterative methods for solving partial differential equations of elliptic type[J].Trans.Amer.Math.Soc 1954,76:92-111.
[3]Bramble J H.Multigrid methods[M].Harlow:Longman Group UK Limited,1993.
[4]Climent J J,Neumann M,Sidi A.A semi-iterative method for real spectrum singular linear systems with an arbitrary index[J].Comput.Appl.Math.,1997,87(1):21-38.
[5]Eiermann M,Li X,Varga R S.On hybrid semi-iterative methods[J].SIAM J.Numer.Anal.,1989(26):152-168.
[6]Hadjidimos A,Stylianopoulos N S.Optimal semi-iterative methods for complex SOR with results from potential theory[J].Numer.Math.,2006,103(4):591-610.
[7]Rayes M O,Trevisan V,Wang P S.Factorization properties of chebyshev polynomials[J].Comput.Math.Appl.,2005,50(8):1 231-1 240.
[8]Belforte G,Gay P,Monegato G.Some new properties of chebyshev polynomials[J].J.Compu.Appl.Math.,2000,117(2):175-181.

