高速船舶远域尾浪的数值计算*
张 伟 高 高
(山东交通学院船舶工程教研室1) 济南 250023) (武汉理工大学交通学院2) 武汉 430063)
0 引 言
从国内目前已投入营运的高速舶舶的航行性能来看,一个较普遍的问题就是尾浪高.过高的尾浪不但会影响航道内其他船只的安全航行,而且会对堤岸造成冲刷破坏,危害水工建筑.因此,如何降低高速船的尾浪己成为船舶工程界及航运部门关注的焦点之一.
就着眼于兴波阻力的数值计算而言,由于兴波阻力一般通过船体表面压力积分得到,人们往往主要关注近域波,特别是船侧波型.最早比较详细计算探讨较远域波型的当推MIT的Nakos在文献[1]中只考虑中、低Froude数下常规船型的波型问题.1994年他又以面元法计算了高速船的船波系、Kelvin波谱及相应的兴波阻力[2].近10a来,高速船尾浪的数值研究与试验预报研究明显增多.A.H.Day和 L.J.Doctor[3]用基于线性薄船理论的帐篷函数法对高速船的近、远场尾浪作了“快速”计算.Amromin等[4]以所谓“准线性理论”计算了船舶及其对环境的冲击.Dimitris等[5]将定常流视为频域中时间-调和流的特例,以传统面元法数值计算了高速单体船的尾浪.Tarafder等[6]以较为经典的面元法及相关数值处理计算了浅水中的船舶问题.
高速船尾浪的有关研究需要探讨相当广泛区域内的船波,从理论上说,只要增大自由面计算域的范围,可以通过传统的面元法计算获得远域波形.但考虑到此方法将极大地增加计算量,目前看来并不可取.1967年,Eggers和Sharma等人提出了波形分析的方法[7],该方法将船后Kelvin波表达成为一元波幅谱函数,以此函数求兴波阻力.Raven[8]利用近域的兴波计算结果计算了远场的波浪.本文根据波形分析的思路,以传统面元法为基础,由近场计算的兴波波形获得波幅谱函数,通过波幅谱函数计算拟合远域的尾浪,计算比较简便而且稳定性较好.文中对于纵切法与横切法的有关探讨,为波形分析在此类问题中的应用提供了有益的参考.
1 数值方法
1.1 船舶兴波问题的数学描述
假定船在静水中做稳定的匀速直线运动,速度为Ū=(U,0,0).取固定于船体上的右手直角坐标系,如图1所示.对于此坐标系,流动为定常,z=0平面为未扰动自由面.假定流体无粘性、不可压缩,则存在速度势Φ.可记Φ=φ-U0x,即总速度势可分解为船舶产生的扰动势与恒定的来流势.

图1 坐标系
扰动速度势φ首先要满足Laplace方程

采用Rankine源格林函数法求解上述方程.在船体表面和自由面(以及所需的浅水或岸壁表面)布置强度为σ的源或汇,则流场中任意一点的速度势可由各个点源对该点引起的诱导速度势表达,对坐标为(x,y,z)的点,扰动速度势写为

式中:S为所有源(汇)分布的表面.
定解条件包括物面边界条件(物面不可穿透),自由面边界条件,远前方无波条件(若考虑浅水或者岸壁限制,则还应包括水底或岸壁不可穿透条件.若考虑方尾,还应包含方尾条件).将扰动势函数的表达势分别代入各边界条件中,就可确定源强σ(q),得到速度势φ.对线性兴波问题,波高ζ可由以下自由面动力学条件得到

1.2 波形分析方法
船行波的一般表达式为

将A(θ)写成A(θ)=g(θ)+f(θ),则式(4)变为
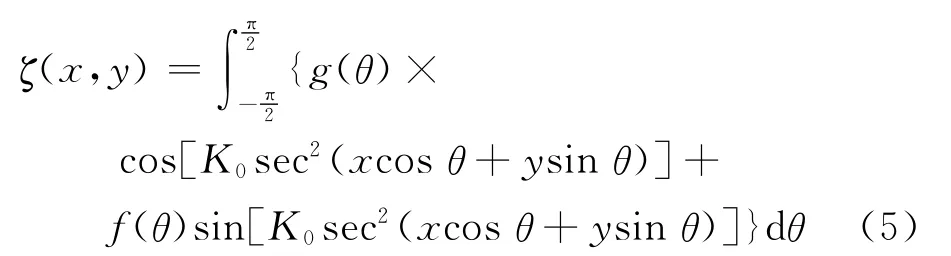
式中:f(θ)和g(θ)分别为正弦波幅谱函数和余弦波幅谱函数.传统的波形分析是利用得到的波浪要素(波高、波浪斜率等)推算波幅谱函数,进而计算波形阻力.本文则是利用该方法,由较小范围自由面兴波问题计算得到的波形求得远域的自由面波形,从而大大减少计算量.令u=K0sec2θ×sinθ;ω=K0secθ,对式(5)进行变量代换,则波高的表达式变为

式中:F(u)和G(u)即为待求量.注意,这里ω也是u的函数,即

波形分析大致可分为横切法和纵切法2种.
1.2.1 横切法 在船后足够远处(例如半个船长),可以认为局部扰动已充分衰减,船行波已近似成为谐波,假定在x=xc处得到的波高为Ex(xc,y),对波高进行傅氏变换得
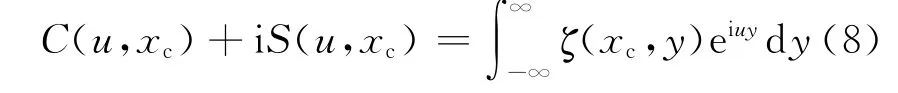
则反变换为
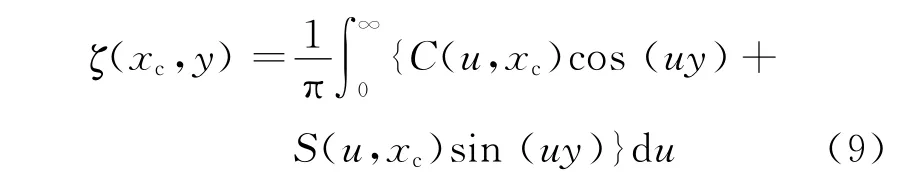
把式(9)与式(6)比较便到方程组
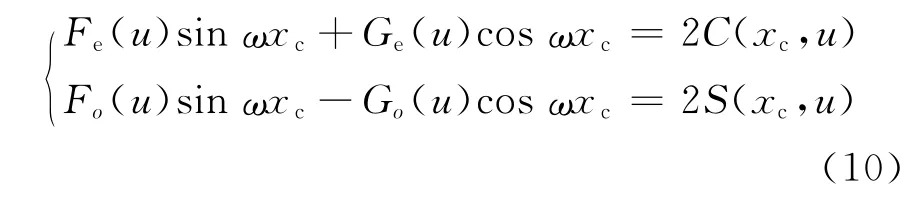
角标e和o分别表示F(u)和G(u)中的偶函数部分和奇函数部分.方程中有4个未知数.为求得其解,可分别在x=x1和x=x2处求取2道波形的波高值,经过傅里叶变换,得到由4个方程组成的方程组.

然而,在作傅里叶变换时,由于u的变化区间是(0,∞),则相应的ω从K0到∞变化,所以不论x1,x2如何取值,总会在若干点处出现分母等于零,造成数值处理困难.因此在实际计算中可多取几道横切波,利用最小二乘法解超定方程,以避免数值困难并减小波形积分计算误差.
1.2.2 纵切法(sharma法) 纵切法的实质是在船侧一定距离y1处,沿y=y1线测量波浪要素,由此导出波幅谱函数,sharma法对y做加权傅氏变换

为了估计截断误差的影响,假定在船的远后方波形的渐进特性为
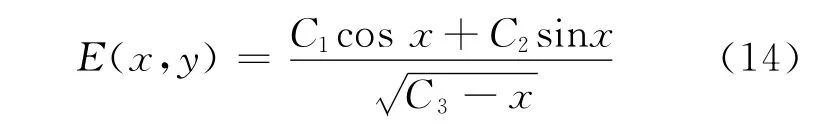
式中:C1,C2,C3均为常数,可在测得波形之尾端取若干点拟合得到.当|xe|较大时,可取C3=0.详细的修正方法见文献[9].
2 数值计算实例
采用Wigley数学船型,以一阶面元法解出近域的兴波波高后,对计算所得自由面作波形分析,进而推出波幅谱函数并获得远域的波浪要素.
为验证所采用方法对于远域波浪计算的有效性,本文将传统的一阶面元法计算的较大范围的自由面兴波结果(下文简称直接法)与由近域计算波形导出的波幅谱函数推算出的远域波浪结果(下文简称间接法)作了比较(后者的近域计算是以一阶面元法对较小自由面范围在同样计算条件下进行的).较大的自由面范围取:船前0.5倍船长,船后3.5倍船长,船侧1倍船长,计算网格为50×10,物面网格为30×10.对较小范围自由面,船后只取1.5倍船长.物面与自由面的网格密度保持不变.通过编程计算,得到结果如下:图2~7分别给出了0.4傅氏数下,面元法直接计算及由波幅谱函数获得的波形图及等高线图,图4、图6中右侧部分为面元法计算得到的波形,左侧较宽的部分为由近域波形分析求得的远域波形(在图5、图7中相应的是方框内的部分).
以下给出离船侧一定距离的直接法计算与间接法波高的比较结果,并对波形分析中采用纵切法和横切法的优劣进行比较.图8图9分别给出距离船中0.3倍和0.5倍船长位置纵切线上的波高与直接法计算结果的比较,本文横切法采用在船后1.0~1.5倍船长范围内取5道横切波.

图2 直接计算波形图(Fr=0.4)

图3 直接计算的等高线(Fr=0.4)
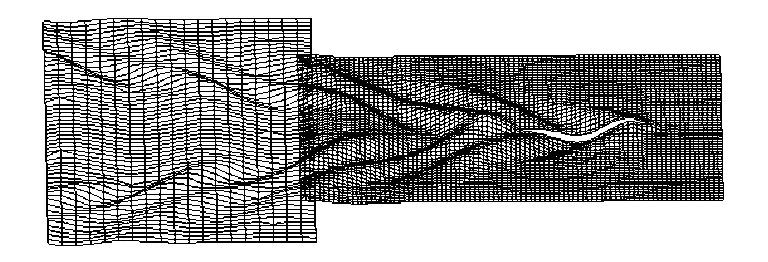
图4 横切法近远域耦合波形图(Fr=0.4)

图5 横切法等高线图(Fr=0.4)
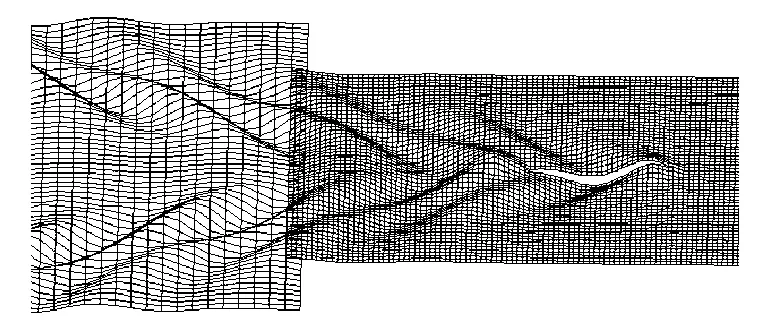
图6 纵切法近远域耦合波形图(Fr=0.4)

图7 纵切法等高线图(Fr=0.4)
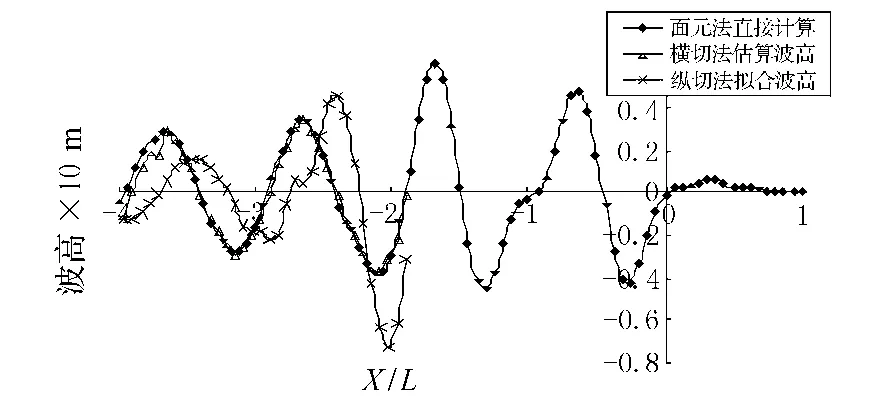
图8 船侧0.3L处的波高情况(Fr=0.4)

图9 船侧0.5L处的波高情况(Fr=0.4)
可以明显看出,横切法得到的结果与面元法直接计算的结果吻合得较好,而纵切法得到的结果虽然也有合理的趋势,但精度较横切法有明显差距.
图10给出了Fr=0.6情况下的相应计算结果,可以看出,横切法得到的远场波在距离船体一定距离之后仍具有较好的精度,而纵切法效果欠佳.

图10 船侧0.3L处的波高情况(Fr=0.6)
纵切法结果较差(尤其在较高傅氏数下)的主要原因很可能在截断误差的处理上.通过调整修正系数及取点范围,纵切法亦可以获得比较好的结果,但不确定性太大.因此,就以波幅谱函数拟合远域波形而言,横切法较纵切法更加适用.就兴波阻力而言,则2种方法结果较为接近,由本文所得波幅谱函数求得的阻力系数曲线见图11.由此可见,对于只需了解尾浪的波能信息的工程问题纵切法仍可用,若需较准确了解尾浪的各要素,则以采用横切法为宜.
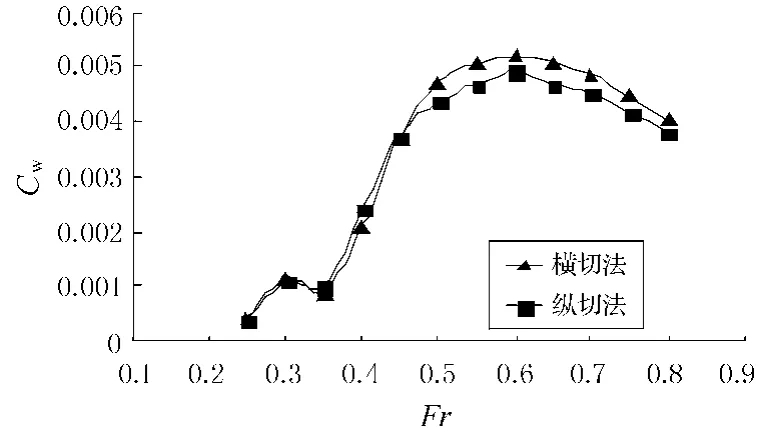
图11 本文由波幅谱函数得到的波形阻力系数曲线
图12、13分别给出了0.4傅氏数下,对 Wigley双体船由波幅谱函数获得的波形图(片体间距为1倍船长,片体间自由面网格取30×10,其他物面与自由面网格不变).可以看出,横切法得到的波形图比较合理,而纵切法由于受到纵切位置的限制,虽在片体外侧可得到的结果合理,但难以反映船后由于片体间干扰产生的复杂波系特征.
最后讨论一下效率问题.以当前常用的微机计算为例,当自由面面元数达到2 000多之后,计算一次约需数小时,本文采用的波幅谱函数计算用时不到3min.
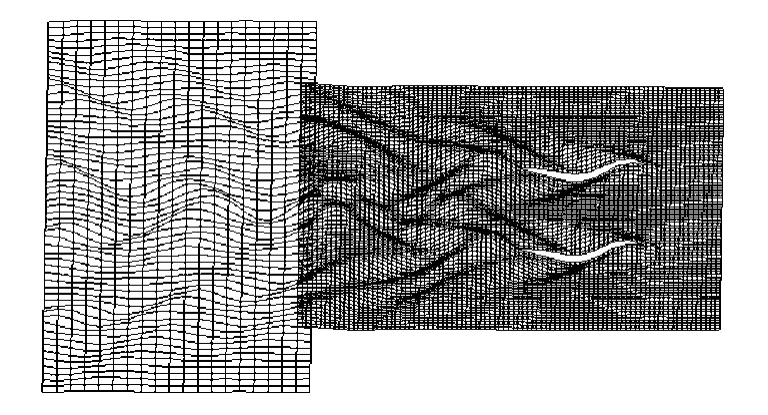
图12 双体船横切波形图(Fr=0.4)

图13 双体船纵切波形图(Fr=0.4)
3 结 论
1)在以面元法作近域兴波计算的基础上,利用波幅谱函数求解远域尾浪的方法可行,计算效率明显提高.
2)对本问题横切法有较好的精度与稳定性,而纵切法计算难以达到较高精度.
3)对多体船情况,纵切法难以反映船后由于片体间干扰产生的复杂波系特征,宜采用横切法.
4)实际远域波的衰减问题今后还需进一步探讨.
[1]Nakos D E.Ship wave patterns and motions by a three dimensional rankine panel method[D].MIT,1990.
[2]Nakos D E,Sclavounos P D.Kelvin wake and wave resistance of cruiser and transom-stern ships[J].Journal of Ship Research,1994,38(1):9-29.
[3]Day A H,Doctors L J.Rapid estimation of near-and far-field wave wake from ships and application to hull form design and optimization[J].Journal of Ship Research,2001,45(1):73-84.
[4]Amromin,Eduard.Quasi-linear theory of ship wave resistance and CFD analysis of ship's environmental impact[C]//Proceedings of the ASME/JSME Joint Fluids Engineering Conference,v 2C,Proceedings of the 4th ASME/JSME Joint Fluids Engineering Conference:Volume 2,Part C,Symposia,2003:2 169-2 174.
[5]Dimitris S,Wash effects of high-speed monohulls[C]//Proceedings of FAST 2005,San Francisco,California,USA.Usenix,2005.
[6]Tarafder,Md Shahjada,Suzuki.Computation of free surface flow around a ship in shallow water using a potential based panel methodKazuo[J].International Shipbuilding Progress,2006,53(1):33-54.
[7]Eggers K,Sharma S D,Ward L M.An assessment of some experimental method for determining the wave-making characteristics of ship forms[M].United States,Office of Naval Research,1967.
[8]Raven H C.Numerical wash prediction using a freesurface panel code[C].RINA International Conference on Hydrodynamics of High-Speed Craft-Wake Wash and Motion Control,London,2000.
[9]李世谟.兴波阻力理论基础[M].北京:人民交通出版社,1986.

