一种基于模式搜索的自学习遗传算法研究＊

姜礼平 胡伟文 吴向君

（海军工程大学理学院1） 武汉 430033） （海军工程大学船舶与动力学院2） 武汉 430033）

0 引 言

遗传算法是一种应用广泛的全局收敛算法，但是传统的遗传算法在复杂优化问题求解中常常力不从心.一些理论研究也证明传统的遗传算法很难收敛到全局最优状态［1］.因此，对遗传算法有众多的相关改进研究.一方面，为了保证算法的全局收敛性，就要维持种群中个体的多样性和搜索的有效性，避免有效基因的丢失；另一方面，为了加快收敛速度，就要使种群较快地向最优状态转移，这又会降低群体的多样性，容易陷入局部最优.如何较快地找到最优解并防止早熟收敛问题是遗传算法中一个较难权衡的问题.

许多研究者提出了各种改进方法来提高遗传算法的性能.其中，针对遗传算法主要算子进行改进和将遗传算法与其他优化算法组合的研究较多.如文献［2］利用选择操作对优良个体的优先遗传作用，通过优化选择策略来提高算法的全局收敛性，这样虽然加快了算法的收敛速度，但也容易产生早熟的问题；文献［3］将量子技术与遗传算法结合，利用量子概率编码的表达多样性，提高了遗传算法解决多目标优化问题的有效性.本文在通过改变编码策略来维持群体多样性的前提下，重点研究了基于模式搜索的学习算子，有效的提高了遗传算法的全局收敛性和收敛速度.

1 模式搜索算法

模式搜索（pattern search）是一种求解优化问题的直接搜索方法.与使用梯度或高阶导数信息来搜索优化点的传统优化算法不同，模式搜索算法在每次迭代中依据模式和步长来搜索当前点周围的一系列网格点，寻找使目标函数值得到改善的点.对于求解目标函数不可微、甚至不连续的问题比较实用［4］.

定义 模式搜索是对当前点按固定模式和步长Δk探索移动（exploratory moves），以寻求可行下降方向（非最速下降方向）的直接搜索法.迭代过程只要找到相对于当前点的改善点，则步长递增，并从该点开始进入下一次迭代；否则步长递减，在当前点继续搜索.以下为模式搜索算法的主要术语及其实现方式.

1）模式 在模式搜索中，模式是若干向量的集合，向量由算法来使用，以确定在每次迭代中要搜索哪些点.例如，如果在某优化问题中存在2个独立变量，则缺省模式由下面的向量组成

2）网格 在每一次迭代中，模式搜索算法搜索一组点（称为网格（mesh）），以寻找使目标函数得到改善的点.该算法形成网格的方法是：（1）给模式向量乘以一个标量（称为网格尺寸（mesh size））；（2）把结果向量与当前点相加.当前点是在前一步找到的具有最佳目标函数值的点.

需要说明的是，模式搜索中用2个变量来调整网格的扩张和收缩，分别为：扩张因子（expansion factor）和收缩因子（contraction factor）.

3）判决 在每一步迭代中，算法通过计算当前生成的网格点的目标函数值，若找到使目标函数得到改进的点（即判决成功），就将网格尺寸扩大进入下一迭代过程，网格扩大的倍数由扩张因子决定，此称为模式搜索的正向机制；同样，若某次迭代中判决不成功，则保留当前点不变，将网格尺寸缩小并进入下一迭代过程，网格缩小的倍数由收缩因子决定，此称为模式搜索的负向机制.具体判决过程中有一个完全表决（complete poll，cp）参数，用来控制判决的完全性.若cp＝1，则判决过程必须搜索、计算并比较每一个当前生成的网格点，寻求其中的最优点替代当前点；若cp＝0，则只要判决过程找到一个相对更优的点就停止当前代的判决过程，以此点作为新的当前点进入下一个迭代过程.

2 基于模式搜索的自学习遗传算法

2.1 自学习遗传算法

总体上讲，遗传算法主要存在两种机制：遗传和进化，遗传是必要的，而进化才是优化的目的所在.绝大多数遗传算法的研究集中在对算法自身的改进和融合上，只考虑了生物遗传的客观性和同代种群个体之间的交流，往往忽略了生物遗传的主观能动性和种群进化过程中前后代累积的经验信息［5］.所谓自学习遗传是指在不改变遗传算法主体的前提下，充分利用遗传过程中的主要遗传信息来指导遗传过程下一步的进化方向，实现主动的自我学习和调整.如文献［5］研究了一种通过统计历代最优解的每一个基因位的累积变化情况来确定当前优化方向的自学习遗传算法.

本文提出了基于模式搜索的自学习遗传算法（active learning genetic algorithm with patern search，ALGA）.即利用每一代遗传中最优个体的变化规律，通过模式搜索的确定型自调整机制，来试探在当前代最优解的附近是否存在进一步优化的空间，并将通过模式学习调整而搜索到的更优解返回当前迭代种群，从而指导遗传算法改善下一步的进化方向，使下一步的个体不断向更优的“先辈”学习.

2.2 基于模式搜索的学习算子

2.2.1 模式搜索作为学习算子的可行性

模式搜索是一种直接、有效的主动搜索方式，具有很强的局部搜索能力和一定的全局搜索能力.而遗传算法具有较好的通用性和全局搜索能力.同时，遗传算法本身不是确定性的搜索机制，这既是优势也使其在遗传过程的优化方向上（尤其是部分种群个体）存在一定的随机波动；并且在已有的遗传选择域内，交叉和变异的局部收敛性远不及模式搜索；特别是在某些特定情况下（如最优域空间相对狭小等），遗传算法存在后期收敛迟滞的问题.因此，在遗传过程后引入模式搜索的学习机制具有很强的可行性.

当然，模式搜索作为学习算子也有相应的应用范围.其对具有连续意义的优化问题编码有较好的应用价值，能很好的增强遗传算法的局部寻优能力，提高收敛速度.而对于互不关联的平行编码或无前后意义的符号编码类优化问题则效果不明显.

2.2.2 学习算子设计流程

本文中模式搜索仅作为局部辅助搜索，因此在本文算法中仅基于模式搜索的正向机制（即只采取扩张模式）来设计自学习算子，其具体设计的简化流程如图1所示.

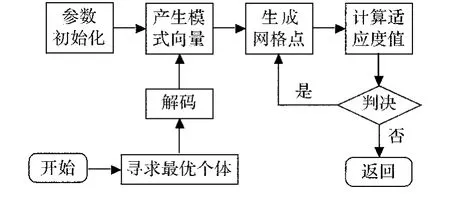
图1 自学习算子设计流程

2.3 基于模式搜索的自学习算法流程设计

综合上述研究，本文基于模式搜索设计了独立的学习算子，提出了新的自学习遗传算法.其基本流程如图2所示.

图2 自学习遗传算法基本流程

下面将基于模式搜索的自学习遗传算法的流程作简单介绍.

1）在本文自学习遗传算法中，初始种群采取标准二进制编码，当然也可采用格雷编码、整数或实数（浮点数）编码，但是主要针对连续性数值优化问题.前期对于初始种群的多样性调整对算法的全局收敛性至关重要，对不同的编码方式和优化问题，需要作针对性的调整.本文中针对标准二进制编码，在考虑种群规模、编码位数、编码区间后，取编码前5位来划分寻优子空间，即可将编码空间划分为32个子空间，确保初始个体在每个寻优空间均存在.

2）在遗传算法的主要操作上，本文中种群适应度取对优化目标值的线性标定值；选择操作采取随机遍历抽样，此方式相对于轮盘赌原则，其选择的多样性要优于后者；变异操作采取离散变异方式，而交叉操作则采用基本的单点交叉模式；在重插入环节，基于适应度和精英保留的重插入可以确保各代中的优良个体顺利的保留下来.

3）主要遗传过程结束后，自学习算子将依据模式搜索机制对当代种群的的最优个体进行趋势调整，判断其下一步优化方向并返回调整结果，这样能很好的提高遗传算法的局部搜索能力.需要说明的是，自学习遗传算法是根据确定的学习机制，从截止当前的种群进化过程中判断种群优化的可能方向，进而在存在优化空间的方向上对目前种群较优个体进行调整并返回优化结果，此过程独立于遗传操作.这有别于自适应遗传算法中依据种群进化进程动态调整遗传参数的方法.

2.4 对遗传过程的适当改进

从上述分析不难看出，自学习遗传算法具有很强的局部搜索能力，能够确保只要进入搜索范围的最优解都能得到体现，但是如何确保在遗传的最终结果中得以体现呢？同时，基于模式搜索的自学习机制在提高遗传算法的局部寻优能力的情况下，是否会同样存在未成熟收敛的风险呢？所以，为较好的解决以上两种隐患，本文在遗传过程上作了三点改进来扩大遗传搜索的全局性和种群的多样性，确保在历代中体现的最优结果得以保留.改进分别为：（1）对初始种群进行分布多样性调整（即划分搜索子空间）；（2）取相对较大的交叉和变异概率，以扩大种群的搜索能力；（3）采取精英保留的重插入策略，确保了最终寻优结果的有效收敛.

3 算例测试

3.1 关于测试的相关说明

对本文设计算法的有效性测试采用两个经典函数，分别为一元多极值函数f1和多元多峰函数f2（Shubert函数）.

式中：函数f1为周期震荡函数，在当前限定域中，当x＝3.9585时取得极小值－1.9584；函数f2是一个多峰值多极值函数，在其定义域内它总共有760个局部最小点，其中有18个是全局最小点，全局最小值为13.2691.测试中参与对比的算法为：标准遗传算法（SGA）和本文的ALGA算法.以下实验为进行最小值寻优且所有数据和结果都在同一计算机环境上同段时期运算所得，具体见表1、图3和图4.遗传算法均迭代30代，其最终收敛是指优化结果在极值点附近，误差控制在1%以内，超出此误差控制范围即认为不收敛，且表1的统计结果为50次连续操作取得.其中，平均收敛代数和收敛均值都是依据在50次遗传中算法收敛的次数及其收敛结果来计算的，平均运行时间为50次遗传的总体运行时间的均值.

表1 算法优化性能统计分析表

图3 算法在函数f1时的收敛情况

3.2 测试结论

从图3～4的算法收敛性对比以及表1的算法优化性能统计结果可以看出，在算法的初始基本参数一致和相同运行环境的情况下，可以得出如下结论.

图4 算法在函数f2时的收敛情况

1）总体而言，ALGA算法的改进使其在优化性能上较SGA算法有很大的改善，充分体现了ALGA算法的有效性.

2）具体上讲，在多极值优化问题中，SGA算法容易陷入局部最优（见图3），基本上不具备解决复杂优化问题的有效性.而ALGA算法具有很高的收敛效率和收敛速度，说明算法对于解决此类问题具有较强的可行性.从表1的平均运行时间比较来看，新算法对程序在执行效率上的影响很小，这主要得益于新算法更快速、有效的收敛性能提升了程序的遗传速度.

4 结束语

本文主要从引入基于模式搜索的独立学习算子对遗传过程进行自我调整.实验结果表明，该算法较好的改善了遗传算法全局收敛的有效性，对于遗传算法在复杂优化问题上的应用提供了一种新的解决思路，具有一定的参考价值.

［1］Rudolph G.Convergence properties of canonical genetic algorithms［J］.IEEE Trans.Neural Networks，1994，5（1）：96－101.

［2］Thierens D，Goldberg D.Elitist recombination：an integrated selection recombination GA［C］／／The First IEEE Conference o－n Evolutionary Computation，USA，Orlando，Floride，1994.

［3］邹 谊，魏文龙，李 斌.多目标量子编码遗传算法［J］.电子与信息学报，2007，29（11）：2 688－2 692.

［4］雷英杰，张善文，李继武.MATLAB遗传算法工具箱及应用［M］.西安：西安电子科技大学出版社，2005.

［5］聂 冲，王维平，赵 雯.基于学习算子的自学习遗传算法设计［J］.计算机仿真，2006，23（9）：168－171.