有源周期性结构缩减表面RCS的研究＊

周 焱 苏东林

（北京航空航天大学电子信息工程学院 北京 100191）

0 引 言

飞行器的隐身研究是现代空战的重要研究课题，而如何有效地将其表面散射的电磁波减少到最小的程度，即有效缩减表面雷达散射截面（RCS）是其中的难题.现在主要应用于缩减物体RCS的技术主要分为外形减缩RCS，选用非金属材料以及采用反雷达涂层等三类［1－2］.

周期性结构，即光带隙（PBG）目前被广泛地应用在微波电路、光纤通信以及纳米材料的设计［3］.而频率选择表面（FSS）也是一种近年来发展迅速的周期性结构表面，主要是针对雷达反射截面（RCS）的减缩而发展的，它具有角度／频率变化特性，带通／带阻特性，典型的窄带特性以及二维结构的周期性［4］.

采用近似高阻抗结构表面的结构形式，利用有源器件变容二极管控制金属单元贴片间的电容，有效改变电控层内的电学性质，吸收入射到表面的电磁波，从而有效缩减RCS是一项有效地隐身方法.而与吸波材料，飞行器外形共形设计的良好结合更是其研究发展的优势［5］.

本文从探讨有源周期性结构减缩RCS的原理出发，研究其工作本质，并通过在仿真验证其理论的正确性和有效性.

1 周期性结构减缩表面RCS原理

1.1 高阻抗表面结构及其有源电控方式

高阻抗型周期性结构是今年来PBG研究的热点之一［6－7］，如图1，高阻抗结构（HIS）可以看作铺设在介质层上表面的周期性金属贴片结构和下表面的金属地通过一个个通孔相连接而构成的类似“蘑菇”形状的周期性结构.通孔的长度和介质层的厚度一致，一般为λ／4，由于下表面的金属地为短路状态，则由阻抗变换的原理可知，上表面的周期性贴片金属单元结构所呈现的电路状态是开路状态，即高阻抗状态.

通过对高阻抗表面的某些改进，可以有效的建立电控周期性结构的模型，如图2所示.将每个金属单元与相邻金属单元间以变容二极管连接，正负极连接方式，将二极管负极所连接的金属单元中间的通孔结构直接透过金属地平面并将通孔壁与旁边的金属地隔离开，用以连接外加电控源.与二极管正极相连接的金属单元中的通孔保持和金属地面接通.这样的结构可以以电位差的形式驱动变容二极管的容值变化.变容二极管的容值变化不仅改变了周期性结构的等效LC网络，也很大程度上影响了电介质层的电参数，从而使得入射电磁波的性质产生了改变.

介质基板的厚度小于λ／4一样可以对减缩RCS产生明显的效果，而且在有源变容二极管加在贴片单元上的时候，通孔的长度被有效缩短，也是可以减薄基板的原因［8－9］.

图1 高阻抗型周期性表面结构（矩形单元）

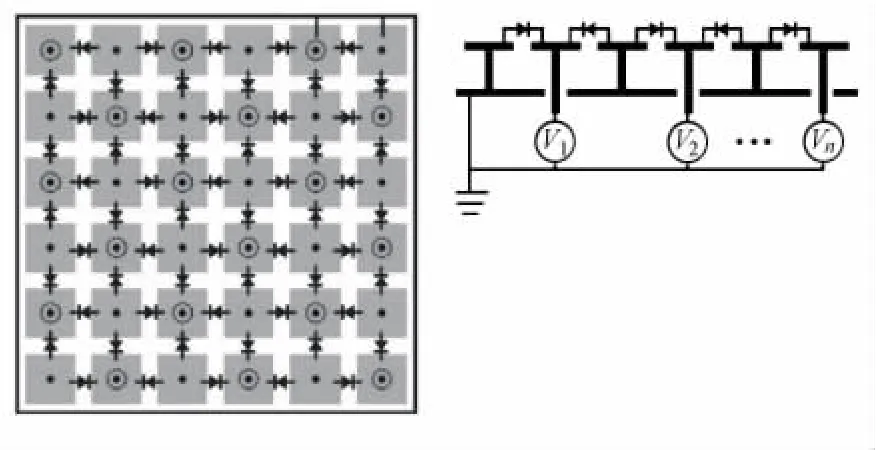
图2 有源控制单层高阻抗型周期性表面结构

1.2 有源控制周期性结构减缩RCS的方式

周期性结构尤其是高阻抗型周期性结构，可以影响介质层的有效介电常数，由公式

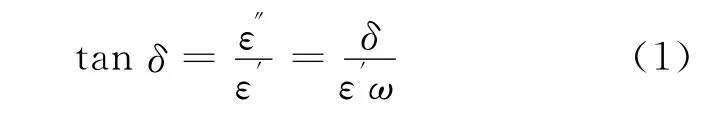
从而改变电介质的损耗角正切tanδ，使得入射的电磁波中的相当一部分被介质层吸收和损耗掉，从而降低了电磁波散射的能量，降低了RCS.在周期性单元间铺设变容二极管来控制有效介电常数的实部和虚部的变化，从而可以控制tanδ，控制降低RCS的幅度以及角度范围.

同时周期性结构表面在一定的频率范围内，可以使得机身表面对于入射的电磁波呈现出一种类似粗糙平面或海平面似的效果，可以使得入射电磁波的散射类似一定程度上的漫反射效果，有效降低单站RCS.

2 有源电控原理

2.1 电介质材料产生吸波能力原理

研究周期性结构对电磁波的吸收，可以先通过探讨多层电介质材料结构反射系数来反映.理想的电介质吸波性能可以用以下方程式表示：电场和磁场的切向元素必须在交界面上是连续的［10］.如果反射参数是

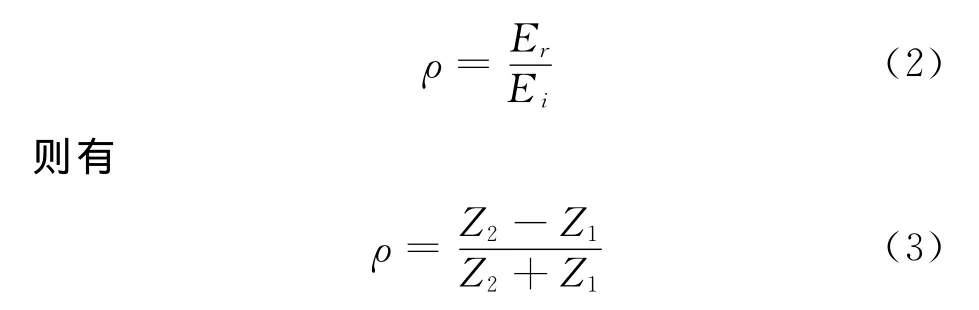
在无耗媒质中，阻抗可以用相对介电常数和导磁率表示出来

如果媒质1是空气或自由空间，则理想的吸收材质为零反射系数.换而言之，比如理想的吸收材料具有参量εr2，与μr2相等.然而，在微波频段，εr2的幅值通常无法达到μr2同样的水平.而在吸收材质中，一些材料可以从通过它们的电磁波的电磁场中吸收一部分能量.

考虑到媒质的电导率，则有阻抗的公式

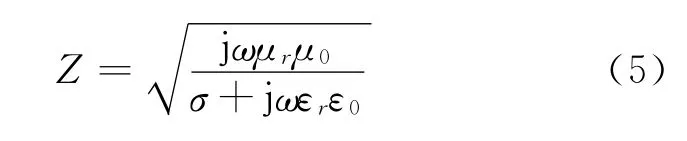
所以无论是吸波材料还是周期性具备吸波能力的结构电路，其基本设计思路就是电介质或磁介质的安排设计以提供合适的阻抗，降低散射波，从而缩减了表面RCS.

2.2 电控周期性结构对电磁波的吸收研究

对于类似高阻抗结构的周期性结构单元的组合，可以将其起决定作用的电容和电感值近似归结到周期性结构贴片单元之间的耦合电容和通孔的电感上.

分析周期性结构单元，以单层单个单元为分析对象，将与地面的通孔也看作水平方向上的一层周期性结构，则单层HIS结构意味着两层周期性结构，同时这样的矩形单元主要是一种电容性的结构，整个电磁性能受到单元间耦合电容性能的制约，分层示意图如图3所示.

2.2.1 上层周期性单元层 对于上层，也就是周期性金属贴片层，依靠自由空间到PBG单元结构内部的阻抗推导，我们假设入射电磁波为TE模式，如图4所示，可以得出，沿x方向的相对磁导率为

图3 周期性结构分层示意图

式中：a为周期单元距离，就是PBG结构的周期；h1为PBG金属层的厚度；g为单元间距.方向介电常数是受到周围平均介电常数影响的.式（6）说明，沿光轴方向的磁导率是横向介电常数的倒数.可以这样说，结构本身聚集了入射的电场，抑制了磁场.这样的结构可以导致TEM波沿着单元的纵向方向传播，就象是多导体传输线.其中，电场分布在每一个单元的边缘部位，磁场被束缚在单元的中间介质层和金属之间.有效介电常数会随着聚集在条带边缘的电场能量的增加而升高，同时有效磁场强度则同时同比例地减小了.而这两项因素是控制波速的，波速一定时，很容易证明这样的相对变化.同时可以清楚地看到，波阻抗发生了很大的变化.而对于控制来说，控制PBG单元之间的金属块的间隙是最明显的几何变化量，同时也是最好地改变磁导率的变量.

2.2.2 下层通孔层 通孔阵列可以看作是周期性平面结构，而这样的阵列可以看作是一种介质层空气柱的周期性排列.如图5所示，在顶层加负电压的情况下，地面到顶层的电场方向如图5所示是朝向上面的，而对于单个通孔和顶面金属PBG单元结构，又可以将它们看作是微带天线的形式.

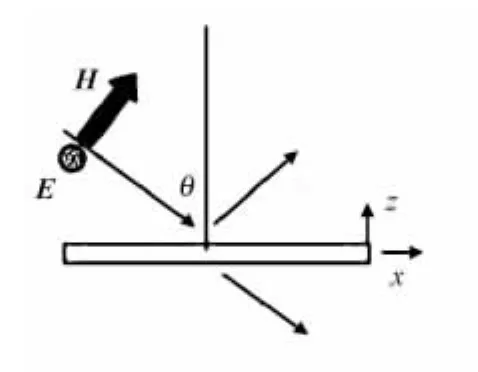
图4 TE波入射情形

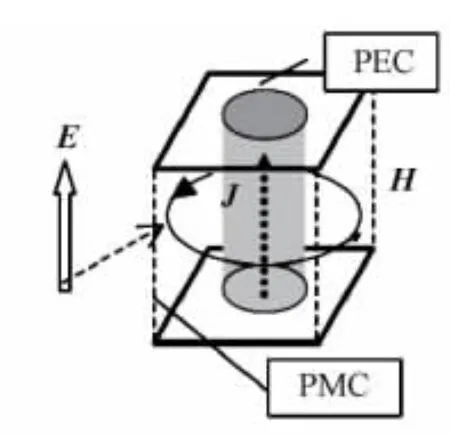
图5 通孔层模型

而整个平面看作一个个“蘑菇”形状的贴片天线阵列，惟一不同的是天线是馈电从下面馈入.而我们的结构是没有馈电的.中间的通孔可以看作一段直导线，在其中加以电场的情况下，有电流生成，因而产生磁场.

分析此通孔单元，可以看做高电感性结构.可以通过磁场计算其电感值的估计为［8］

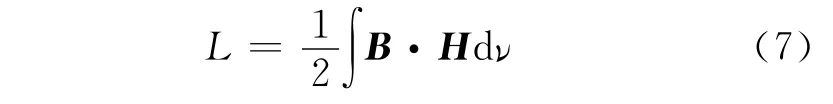
在低频的条件下有［8］

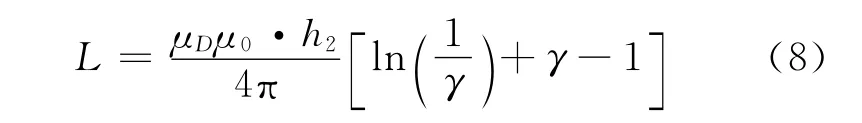
式中：γ为填充率.有了电感的估计值，可以通过试验手法确定通孔周围的介电常数和磁导率.从而得出z方向的有效介电常数为［8］

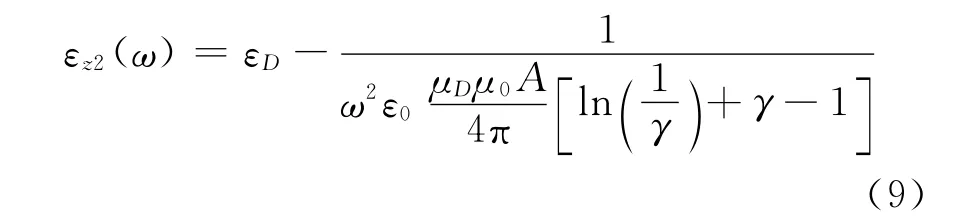
式（9）是在低频的情况下的近似，是相对于周期性结构所无法起作用的很高的频率所定义的.故有一个截止频率，高于截止频率就呈现出开路的性质了.对于这样的金属－电介质－通孔结构，其ε的主要作用源就是填充率和单元的尺寸，这两项元素并且影响其截止频率.

而事实上，有效介电常数是可以将电磁波在平面表面所传播的表面波负数率控制的.换句话说，就是比如假设介电常数从－10变为－5，则在这个频段的表面波是被截止的.而对于整个系统来看，则表面波在一定频段内被抑制了［9－10］.

3 实验仿真

针对普通的微波基板材料，来仿真实验有源周期性结构对RCS的减缩性能.在HFSS中模拟出变容二极管的变容能力，可以针对变容二极管在整个系统中所起到的主要作用，用一个无源实体来代替，并且设此实体的介电常数可变，通过以上的分析，可知介电常数的改变直接影响了其电容的变化，这样一来，就用无源的实体模块模拟了有源的二极管器件，如图6所示.

图6 在HFSS中模拟有源周期性结构的方法

第二种方法是，直接在整个周期性结构模型中，改变电可控层的矩形贴片的尺寸，原理也是间接改变了其之间的耦合电容，只是这样的改变是对于仿真其性能而假设的改变，实际情况下是无法实现的.

基于以上方法，分别对不同层数的有源周期性结构进行HFSS分析，对于变容二极管的容值变化范围取通常的3～20pF，这里暂时不针对任何实际型号的二极管，只取普通的变容量程座作为代表性研究.同时对应的模块ε值的虚部为0.2～0.7的变化范围.而对于多层的周期性结构采用第二种方法变换各层金属贴片的尺寸模拟互相连接变容二极管电容的容值变化，或2种方法结合使用，幅度在±40%以内.同时仿真各结构单站RCS值，取设定范围内各变化参数来体现在缩减RCS上的作用.由于基片设计采用的是εr＝10.2，所以在周期为5mm时，其周期性结构的基本谐振频点在7GHz附近.见图7～8所示.

图7 从整个表面上取出其中一个5mm×5mm的单元在HFSS上建立周期性边界条件仿真

下面就平面金属、单层有源周期性结构、双层以及三层结构分别加以仿真，所有结构取5mm×5mm单元.

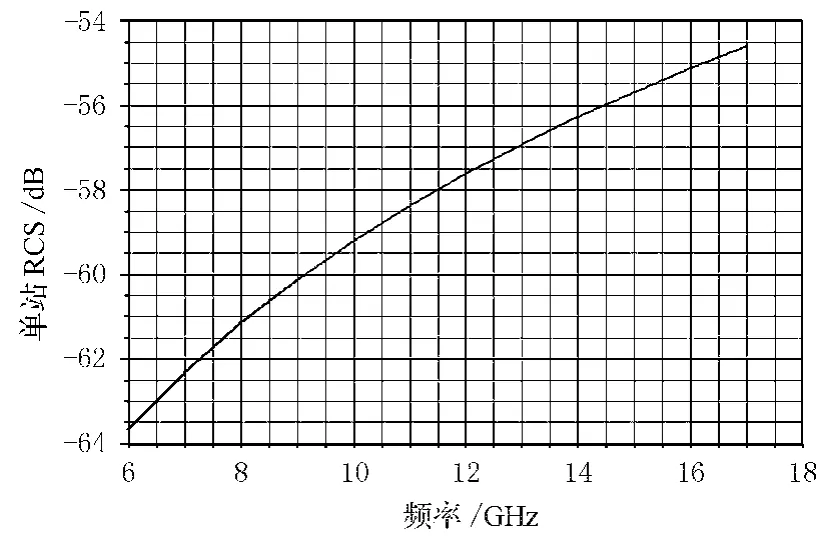
图8 单站RCS仿真结果

理论仿真结果表明：单层有源周期性结构可以使得RCS缩减了65－62.3＝2.7dB（7GHz），而采用的双层和三层有源控制周期性结构分别有能力在工作频率点7GHz上将单站RCS降低了77－62.3＝14.7dB和86.5－62.3＝24.2dB.这是仿真的数据，实际情况下可能会有很多不理想的条件，结果会有差异，但仿真结果的趋势是可以说明问题的.

在控制变容二极管的容值使得缩减RCS效果产生变化的同时，吸收频带也发生了变化（图9中的各条曲线频点变化明显，图10中频点都已经降低到7GHz以下）.但所有的仿真试验都是建立在HFSS理想的条件下，而在目前国内的多层高频板的工艺各项条件差距比较大，而且加工精度无法达到这么高的情况下，无法制作实际的实验件测试得到进一步的第一手数据资料也是比较可惜的.

图9 双层矩形周期性结构RCS

图10 三层矩形周期性结构RCS

4 结束语

通过对有源周期性结构对介质层电参数的改变影响，以及系统的RCS对比仿真分析.可以知道在类似高阻抗结构的上层金属单元间铺设变容二极管，有效地改变了电控层的电学性质，使得整个表面结构产生了吸收电磁波的效果.同时有源周期性结构表面还在吸收和抑制表面波等方面对减缩RCS作出了贡献，并且其与吸波材料以及共形的结合能力也很强.综合多项性质，可知有源周期性结构可以很好的用在飞行器或其他物体的隐身、减缩RCS等用途上.

［1］理查森 D.现代隐身飞机［M］.北京：科学出版社，1991.

［2］Fulghum D A，Wall R.Russia＇s top designers claim antistealth skill［J］.Avitio Week ＆Space Technology，2001，10（8）：82－85.

［3］John D，Robert D，Joshua N.Photonic crystals［M］.New york：Princeton University Press，1995.

［4］侯新宇，万 伟，佟明安.带有多层介质衬底FSS的损耗和带宽特性分析［J］.微波学报，1999，15（4）：366－370.

［5］卢 俊，高劲松，孙连春.吸波材料与频率选择表面复合的实验研究［J］.光机电信息，2003（9）：5－8.

［6］Simovski C R，Peter de Maagt，Melchakova I V.High－Impedance Surfaces Having Stable Resonance With Respect to Polarization and Incidence Angle［J］.IEEE transactions on antennas and propagation，2005，53（3）：908－914.

［7］Sievenpiper D F.High－impedance electromagnetic surfaces，a dissertation submitted in partial satisfaction of the requirements for the degree of doctor of philosophy in electrical engineering［M］.University of Callfornia，Los Angeles，1999.

［8］Sievenpiper D F，Schaffner J H，Song H J.Gregory tangonan，two－dimensional beam steering using an electrically tunable impedance surface ［J］.IEEE Transactions on antennas and propagation，2003，51（10）：2 713－2 722.

［9］Tennant A，Chambers B.A Single－layer tuneable microwave absorber using an active FSS，IEEE microwave and wireless components letters［J］.2004，14（1）：46－47.

［10］Parchomchuk P，Wallender W W，King R J.Direct solution for dielectric properties of a lossy two－layered material［J］.IEEE transactions on geoscience and remote sensing，1989，27（3）：310－315.