基于Pythagorean Hodograph曲线的无人机路径规划方法

李大林，李 杰，杨东晓

LI Da-lin,LI Jie,YANG Dong-xiao

（北京理工大学 机电学院，北京 100081）

0 引言

无人机路径规划一直是该领域的一个研究热点，大多数的路径规划方法（参考文献[1,2]）是通过一些算法将目标区域进行划分，找出节点，无人机沿着节点飞行至目标点。在节点处对其局部路径进行平滑化，使其满足无人机最小转弯半径的需求。此种方法仅在节点处考虑了飞行器的最小转弯半径的约束，没有从整体路径上考虑。因此，路径的曲率变化可能相差比较大，在实际应用中则表现为真实飞行路径与规划路径间的误差较大。文献[3,4]提出使用Dubins路径对无人机进行路径规划，虽然Dubins路径作为前向飞行器所能达到的最短路径，其曲率同样是不连续的，此路径仅优化了路径长度，并没有控制系统需求的路径曲率连续性。

Pythagorean—Hodograph (PH)曲线，即勾股速端曲线，是一种特殊的多项式参数曲线，1990年由Farouki等在研究等距曲线的过程中提出[5]。PH曲线各坐标分量导数的平方和恰好为一个完全平方式.由于具有特殊的代数结构，PH曲线与一般的曲线相比具有重要的计算优势。例如，PH曲线的弧长可以表示成参数的多项式函数，因而可以被精确地计算出来。PH曲线的等距曲线是相对低阶的有理曲线。PH曲线具有精确的弧长和等距线表示，即当它们是多项式或有理参数曲线时，相应的弧长函数、等距线等也是多项式或有理的。

本文提出了一种基于Pythagorean—Hodograph（PH）曲线的路径规划方法，此方法将产生具有连续曲率的无人机飞行路径。应用遗传算法对PH路径、路径曲率标准差以及兼顾二者的情况进行优化，在无障碍平面内得到最短PH路径、曲率标准差最小路径以及兼顾上述二者的Pareto最优路径。

1 PH曲线

曲线r (t)的长度为：

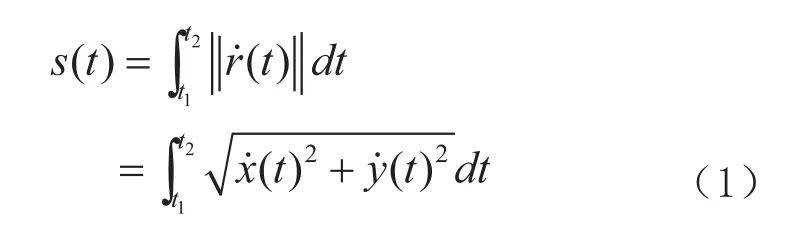
公式（1）中根号内为速度的平方和，如果根号内的项可以表示为多项式的平方，记为σ (t)2，那么式（1）可转换为：

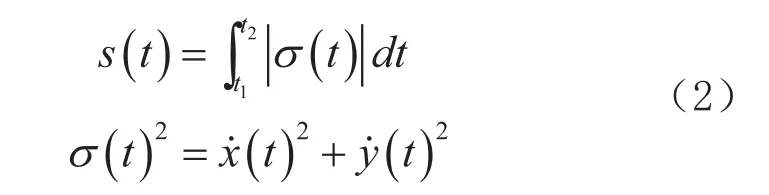
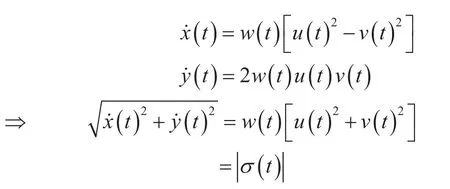
其中，u (t)和v (t)为正素多项式，w (t)＝1，并且σ (t)为n-1次多项式。

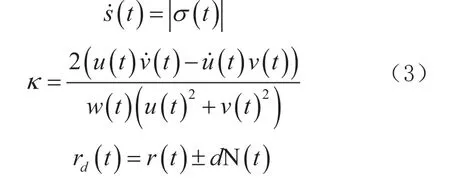
由（3）式可知，PH曲线的参数速率的求解问题可转换为多项式求根问题。曲率为有理形式。

2 基于PH曲线的飞行路径构造

由于PH曲线独特的优点，提供有效可靠的方法来构造、分析和控制PH曲线是非常必要的。因为PH曲线的定义包含多项式u(t)、v(t)等的乘积与平方，所以决定这些多项式的系数使其满足给定的离散数据(点、切向量等等)，必然引起具有多解的非线性问题。

能体现PH行为的曲线至少为三次PH曲线。因为三次PH曲线没有拐点，所以在设计应用中受到限制。与经典三次曲线具有类似的形状复杂度的是五次PH曲线。因此，这里使用五次PH曲线对无人机进行路径规划（以下简称为PH路径）。起始点和目标点位置分别为(xs，ys)和(xf，yf)，对应的方向角分别为θs和θf，这些参数可作为路径的边界值。

为使PH路径具有数值稳定性，这里将其写成Bézier形式。N阶的多项式公式其Bézier形式为：

五次PH曲线能插值任意一阶Hermite数据。在路径的起始点以及目标点坐标和方向已知的前提下，使用一阶Hermite插值。带入t=0和t=1的位置坐标，形成路径的一阶微分，控制点b0，b1，b2，b3，b4，b5可由以下公式计算得出：

曲率计算公式如下：

给定控制点参数的PH曲线以及曲率变化如图1、图2所示。基于PH曲线构造的PH路径与Dubins路径的比较如图3所示。

图1 PH曲线

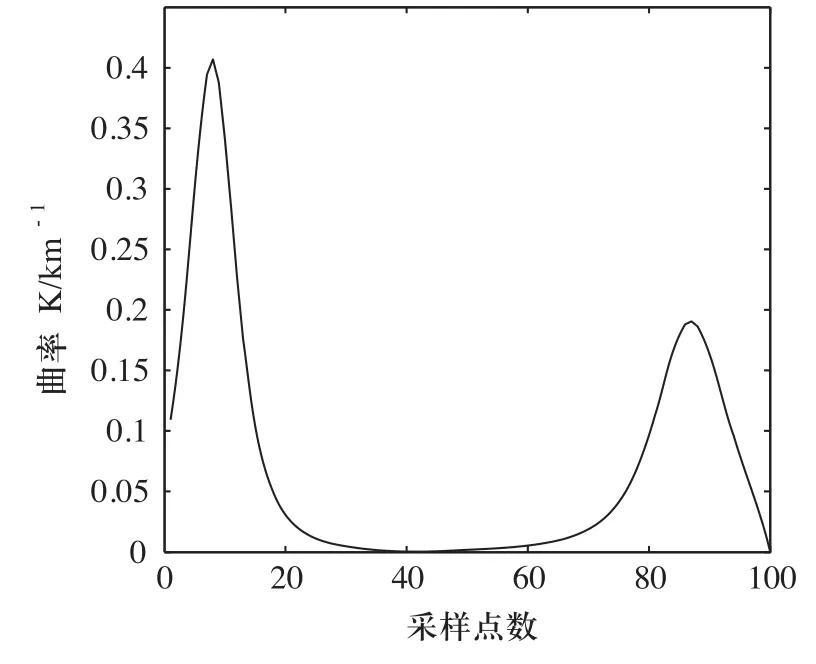
图2 PH曲线曲率变化

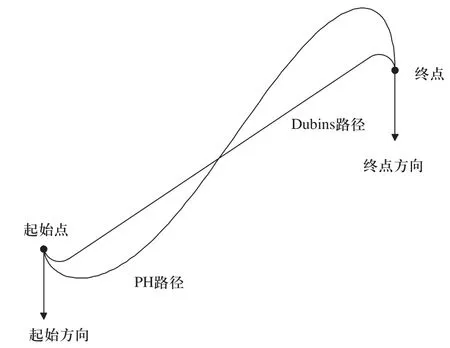
图3 PH路径与Dubins路径比较

现在，问题转换为找到满足PH条件的参数θ1、θ3、n1、n2、n3和 n4值构造适合的 PH 曲线。

3 基于遗传算法的PH路径优化方法

基于以上构造算法，下面进行优化处理。在起始坐标、起始方向、终点坐标以及终点方向已知的情况下，在曲率满足最大曲率限制的条件下，确定6个相关参数对以下三个目标进行寻优：

1） 优化PH路径，使其路径长度最短；

2）优化曲率的标准差，使其路径曲率变化最小；

3）同时优化以上两个目标，找到满足以上两个目标的Pareto最优解。

目标函数分别为：

1）min L(r)即min L(θ1,θ3,n1,n2,n3,n4)

2）min E(k)

3）min (L(r)∪E(k)

约束条件：

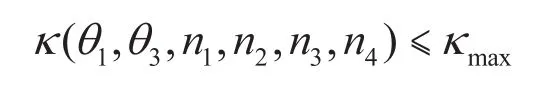
由于参数较多，在一定精度范围内使用穷举法对此问题进行求解，运算量巨大。遗传算法则可大大提升求解此问题的效率。

3.1 遗传算法

Holland创建的遗传算法（GA）是一种概率搜索算法，在许多领域中得到了大量的应用[6,7]。GA可以在可行解决方案的决策状态空间进行有效的搜索。该方法包括可行解种群的迭代操作，称为染色体，来获得更好解的种群。GA染色体编码是优化过程的重要组成部分。该算法包括以下步骤：1）初始化——产生初始种群；2）适应度——评估种群中每个染色体的适应度；3）解算——满足停止条件则停止，否则继续；4）得到新的解——通过遗传算子生成新的候选染色体，从而模拟进化过程；5）替代——用新的染色体替换就得染色体；6）循环——回到步骤2）。

本文采用二进制编码对优化参数（θ1,θ3,n1,n2,n3,n4）进行编码，编码长度分别为θ1,θ3为十位，精度为π/211。n1,n2,n3,n4分别是二十位，前十位为x轴方向对应的参数，后十位为y轴方向对应的参数。精度为500/211。本文使用的是单点交叉算法。对交叉概率pc和变异概率pm设计如下：

其中，ζmax为群体中个体适应度的最大值。ζavg表示逐代适应度的平均值。ζ'为两个交叉个体的适应度的较大值。ζ为变异个体适应度的值。

3.2 仿真分析

本文针对初始位置为（0，0）、终点位置为（100km，20km）、初始方向和终点方向均为-90度的情况进行仿真。

3.2.1 最短PH路径

不考虑曲率方差最短PH路径仿真结果如图4、图5、图6所示：

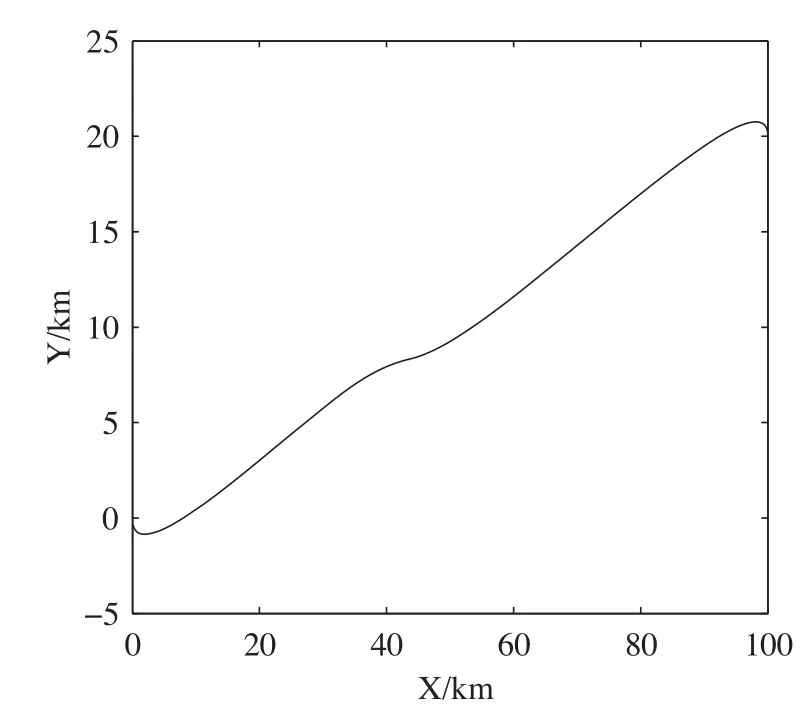
图4 最短路径

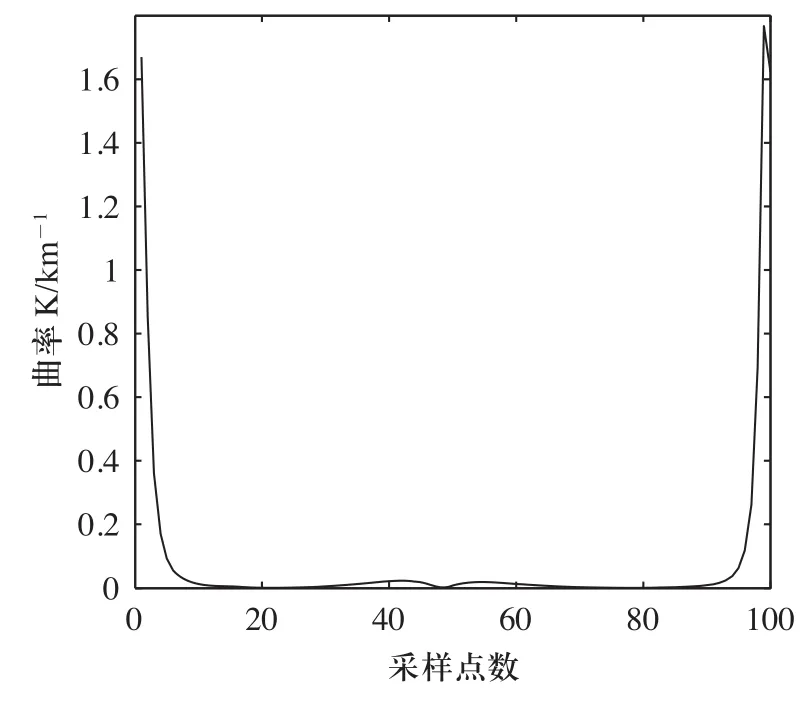
图5 最短PH路径的曲率变化

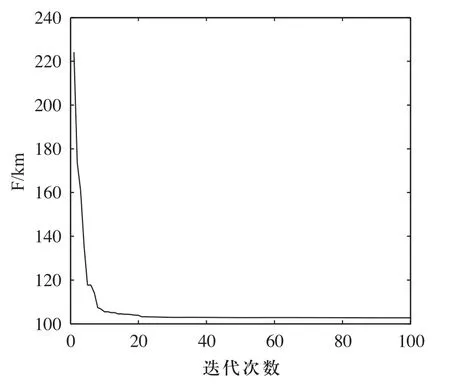
图6 计算PH最短路径的遗传算法收敛曲线

图7 最小曲率标准差情况下的PH路径

图5表明了构造的最短PH路径符合无人机最小转弯半径的约束，即此路径为可飞路径。图6表明了构造的最小PH路径长度收敛在102.8km，具有最短路径特征的Dubins路径长度为102.77km。根据多种情况下的仿真，这里就不一一列举，最短PH路径的长度相比最短Dubins路径长度长出2%。

3.2.2 稳定PH路径

考虑到控制系统的稳定性，要求PH路径的曲率变化应相对平稳，这里用曲率的标准差来表征曲率的变化程度，曲率标准差计算公式如式11所示。

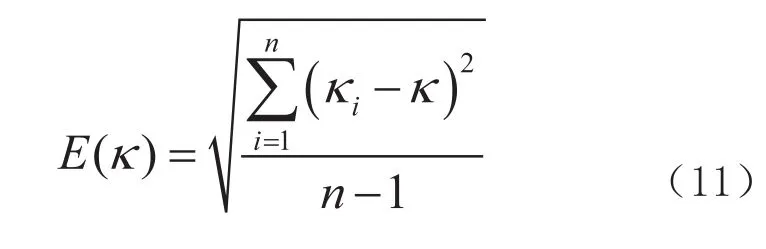
针对曲率标准差的PH路径仿真结果如图7、图8所示。

稳定PH路径仅仅对曲率标准差进行了优化，因此其路径长度较长，仅仅满足控制稳定的需求。

3.2.3 稳定最短PH路径

同时对路径长度以及曲率的标准差进行寻优，属多目标优化问题。对于求解多目标优化问题的Pareto最优解，本文主要使用并列选择法进行求解。先将种群中的全部个体按子目标函数的数目均等地划分为一些子种群，各自选择出一些适应度高的个体组成一个新种群，然后分别进行交叉和变异运算，然后将子种群进行随机合并成一个完整的新种群，如此不断地进行“分割—并列选择—合并”操作，最终可求出多目标优化问题的Pareto最优解[8]。

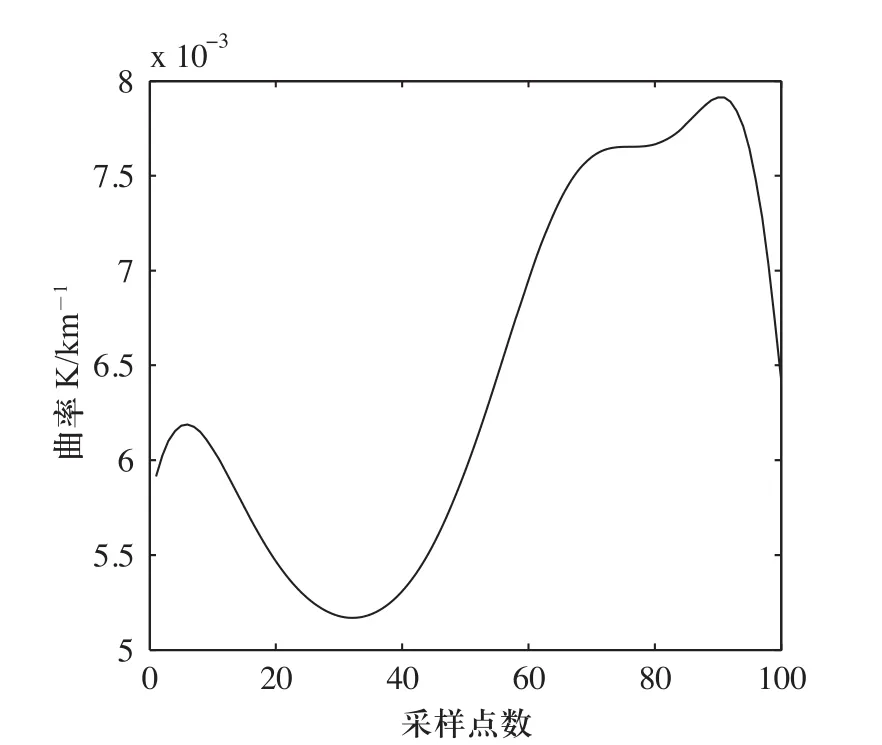
图8 最小曲率标准差情况下的曲率

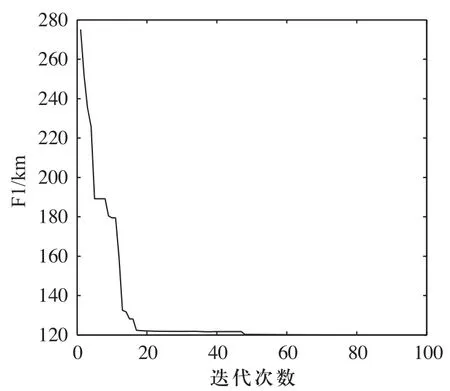
图9 多目标路径收敛曲线

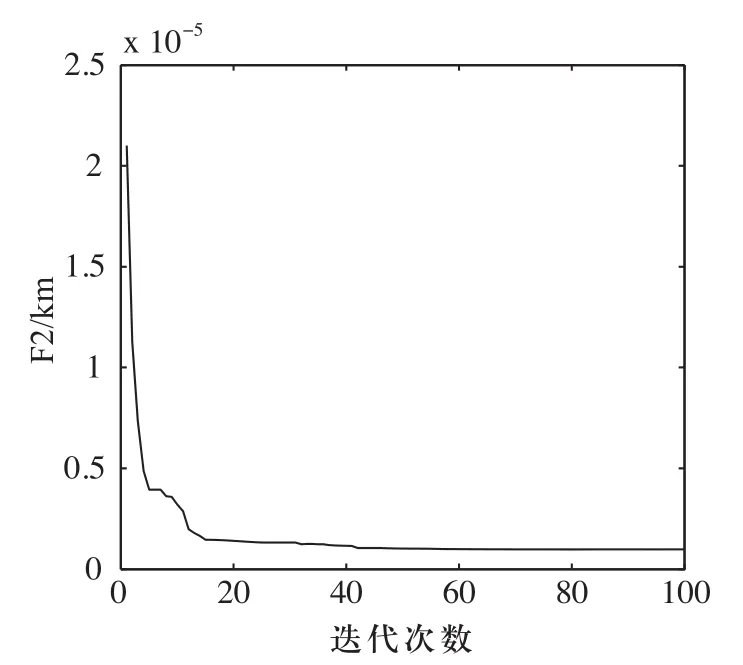
图10 多目标曲率标准差收敛曲线

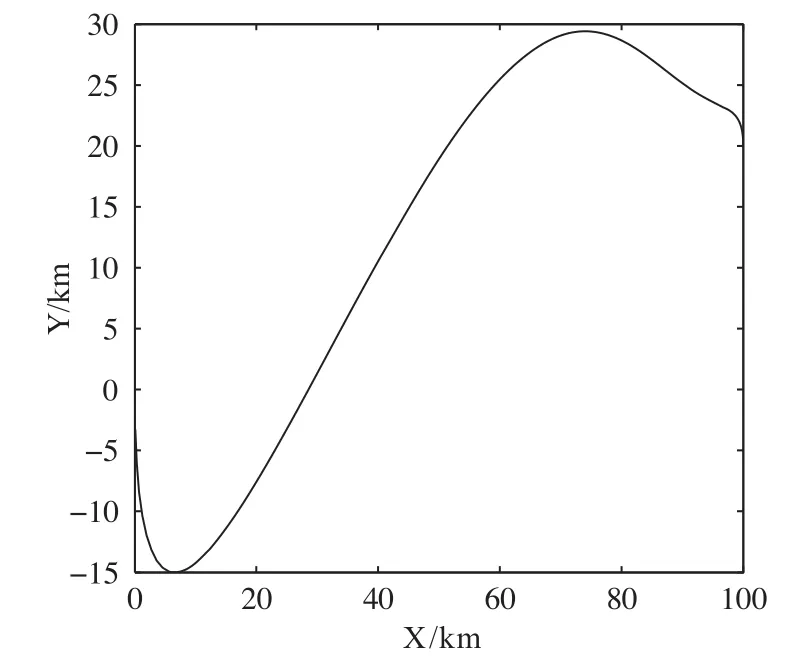
图11 两目标优化后的PH路径

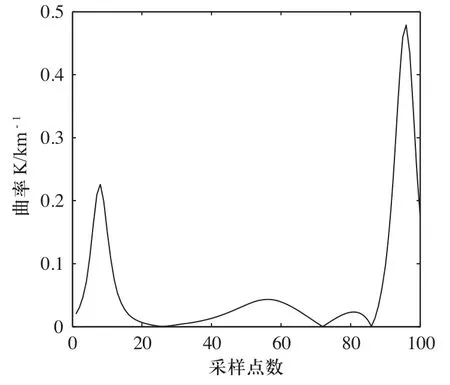
图12 两目标优化后的曲率

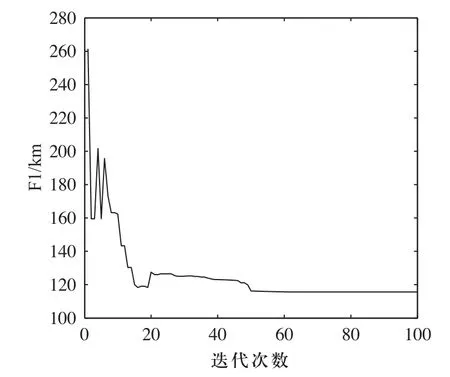
图13 多目标路径收敛曲线2

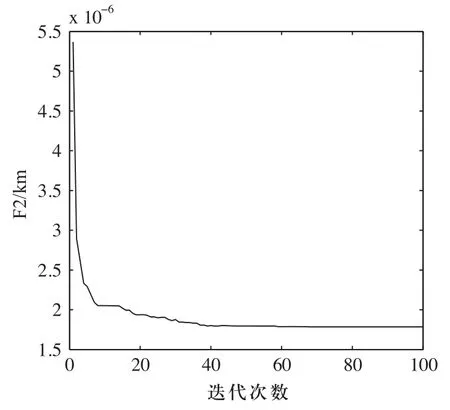
图14 多目标曲率标准差收敛曲线2

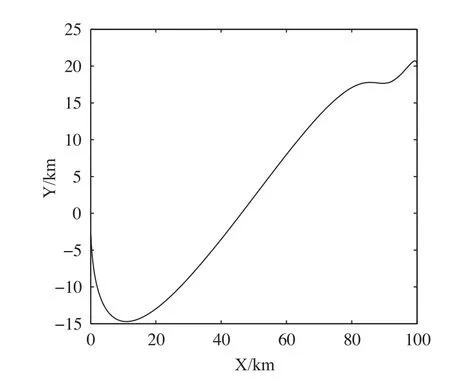
图15 两目标优化后的PH路径2

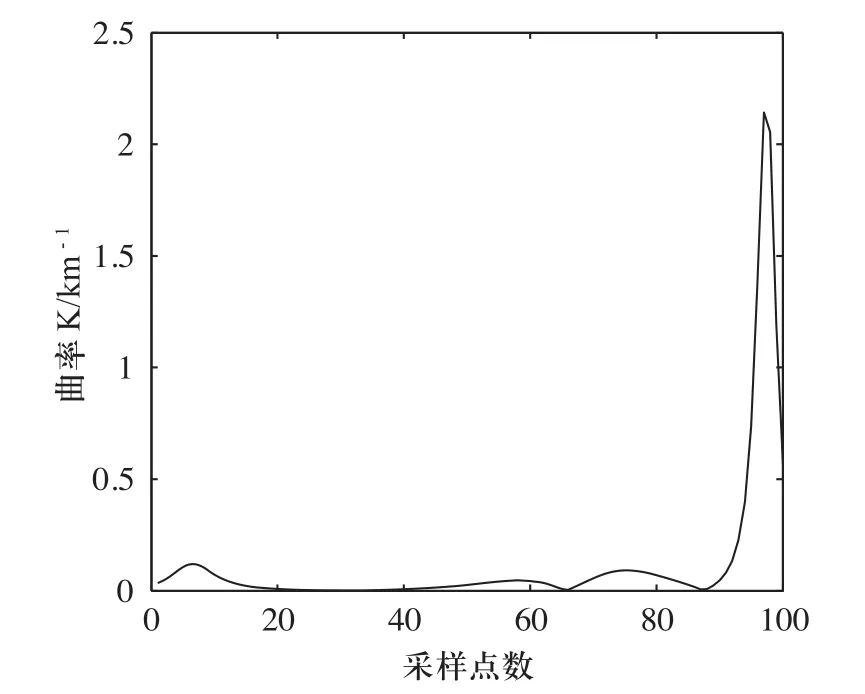
图16 两目标优化后的曲率2

如图9～图16所示，稳定最短PH曲线存在多种情况，Pareto最优解是一个最优解集它是由那些任一个目标函数值的提高都必须以牺牲其他目标函数值为代价的解组成的集合。

4 结论

本文提出了一种基于PH曲线的无人机路径优化规划方法，该方法使用遗传算法对基于PH曲线的无人机路径进行了优化，在无人机最小转弯半径（即曲线曲率的倒数）的约束下，优化的内容包括对最小化PH路径的长度单目标优化、最小化曲率标准差单目标优化、同时最小化PH路径和曲率标准差的多目标优化。仿真结果表明使用本方法可以为无人机提供一种曲率连续且标准差最小，且路径相对较短的飞行路径。

[1] 温瑞,王航宇,谢君,一种移动机器人路径规划方法[J]. 兵工自动化,2009(12)： 60-63.

[2] 毕慧敏,董海鹰. 改进遗传算法在机器人路径规划中的应用[J]. 兵工自动化,2006(4)： 53-54+66.

[3] Savla,K.,F. Bullo and E.Frazzoli. The coverage problem for loitering Dubins vehicles[C].Decision and Control,200746th IEEE Conference.2007. p. 1398-1403.

[4] Chao,Y. and E.J. Barth,Real-time Dynamic Path Planning for Dubins'Nonholonomic Robot[C].Decision and Control,200645th IEEE Conference.2006. p. 2418-2423.

[5] 王琦魁,陈友东,李伟等. 基于PH曲线的数控拐角过渡方法[J]. 航空学报,2010(7)： 1481-1487

[6] 严浙平,黄宇峰,李锋. 遗传算法在AUV局部路径规划中的应用研究[J]. 应用科技,2009(2)： 46-51.

[7] 徐剑,周德云,黄鹤. 基于改进遗传算法的多无人机路径规划[J]. 航空计算技术,2009(4)： 43-46.

[8] 雷英杰,张善文,李续武等. MATLAB遗传算法工具箱及应用[M]. 西安： 西安电子科技大学出版社. 2005.