试论中韩股市收益的动态相关性——基于DCC-GARCH模型

朴 基 石

(延边大学经济管理学院,吉林延吉133002)

一、研究中韩股市收益动态相关性的意义

随着中国金融改革的不断深化及国际资本市场的全球一体化,特别是 QDII及QFII的实施,我国的资本市场与国际金融市场之间的联系越来越紧密,越来越多的国内投资者寻求在国际资本市场组合投资,以实现高收益与低风险的目标。国际资产间的组合投资行为,必然是在不同国家的资产收益及波动间进行权衡。根据组合投资理论,不同资本市场的收益率之间的相关关系与组合投资的风险(分散投资风险的能力)密切相关,因此深刻了解中国与国际股市之间收益的联动性,不仅对于国际投资者有效构造投资组合,分析投资风险具有重要的意义,而且对相关部门监管和预防源自外部的金融危机也具有重要的意义。

随着中韩经济交流合作的不断深入以及近年来中国在资本上的“走出去战略”,资本流动已由单向流入向双向流动转变。源于人缘与地缘上的特点,延边地区与韩国有着广泛的合作与交流,这必然在金融领域里有所体现。特别是在韩工作的中国人员逐年增多,并且这些工作人员的知识结构、理财投资理念也在提升,在中韩两国资产上组合投资不再是投资机构独有的行为,而有平民化的趋势。依此视角,研究中韩两国资本收益的特征与相关关系对个体、机构投资者都具有重要的指导意义。此外,韩国又是金融危机的“易感体”,因此准确把握中韩两国股票市场收益的联动关系,对政府的金融危机管理也具有重要的参考意义。

二、文献回顾

不同市场收益间的相关性(联动性)一直是机构投资者及学者们关心的问题,对国际证券市场间联动性做了大量实证分析。Hamao等人(1990)采用多变量 GARCH模型研究了美国、英国、日本三国股市的相互影响,实证结果发现1987年10月之前,存在从美国股市到日本股市、从英国股市到日本股市、从美国股市到英国股市的单向波动溢出效应。[1]Jang等人(2002)使用格兰杰因果检验和协整方法研究了泰、韩、印、日、新、港、台的股市联动效应,认为1997年金融危机后各国股市的联动效应比较明显。[2]Worthington等人 (2004)采用多变量GARCH模型对1998年1月到2000年10月间香港、日本、新加坡、印尼、韩国、马来西亚、菲律宾、泰国、台湾股票市场进行了分析,并将这些市场分为两类,即香港、日本、新加坡为发达的金融市场,其余为发展中金融市场。分析结果表明,“发达的金融市场”与“发展中的金融市场”存在明显的溢出效应,或称联动效应,但是在发展中市场之间效果不明显。[3]Arouri等人(2008)运用动态相关-条件异方差模型(DCC-GARCH)对拉美6个市场间及这些市场与国际市场的联动性进行了研究,研究表明,拉美市场与国际市场间的联动性还很弱。[4]虽然国际学者对国际金融市场间的联动性问题研究很多,但国内对此研究相对较少。陈守东等人(2003)认为,2003年之前我国股票市场与国际市场联动性很弱。[5]徐有俊等人(2010)将中国股票的影响因素分为国际因素及区域因素,并通过中印股市的对比研究,认为中国与国际股市的联动性较小,但有增强之势,特别是2007-2009年全球金融危机以后更明显。[6]

从已有文献可知,对中国股票市场与国际股票市场之间联动性研究不多,且在这不多的研究中主要针对的是中国与美国、英国、日本、新加坡等大的金融中心,鲜有对韩国与中国股票市场的研究,本文将补充这一研究空隙。

三、DCC-GARCH模型

Engel(2002)提出的DCC-GARCH模型为研究多变量条件异方差问题中所用的最前沿的研究工具之一,在研究国际股市联动性方面应用较多,能够通过金融市场之间的动态相关系数掌握市场间的联动性。[7]

设r为k个观测样本为 T均值为零的时间序列,且服从多元正态分布,如方程(1)所述:

DCC-GARCH模型可用如下式(3)、(4)、(5)、(6)来定义。

上式中 It-1为至 t-1期可用于预测下一期 rt的情报集合(information set),∑t为t期 r的协方差矩阵。根据协方差的定义,∑t可分解为对角化的方差矩阵与相关关系矩阵的乘积,如式(2)。Dt为对解矩阵,其对解上的元素为各时间序列的标准差,Rt为相关系数矩阵。式(3)描述的是各时间序列方差服从 GARCH过程。为了兼顾拟合能力与模型的简洁性,本文直接设定 GARCH(1,1)过程。

上述的DCC-GARCH模型的似然函数(对数)可表述为:

似然函数(7)又可以拆分成波动部分(LV(φ,θ))与动态相关部分(LC(φ))似然函数的和,即LL=LV(φ,θ)+LC(φ) 。

根据Engel(2002)所述,此模型可以采用二阶段方法进行参数估计,首先估计波动部分的参数(φ,θ),即估计式(8)中的参数 ,然后在上一阶段的基础上估计余下动态相关部分的参数,即估计式(9)中的参数。需要说明的是,上述的说明是基于时间序列为正态分布假定上进行的,在序列为“厚尾态(fattail distribution)”时 ,常采用 Quasi-ML E(QML E,也称pseudo MLE)方法估计。本文采用 QMLE方法。

四、实证分析

(一)样本数据选取及其统计特征

本文采用中国上证综指SSE及韩国 KOSPI的周数据系列来分别代表中国和韩国的股票价格指数,研究选取的样本时间为2000年1月的第1个星期到2010年10月的第1个星期。文中所有数据均来源于雅虎金融网(http://finance.yahoo.com/)。收益率的计算以每周五收盘价为标准,并将收益率转化为百分比,即:

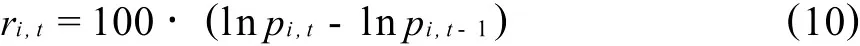
上式中,ri,t代表i股市t期的年收益率,pi,t代表i股市t期的价格指数,i为中国或韩国股市。

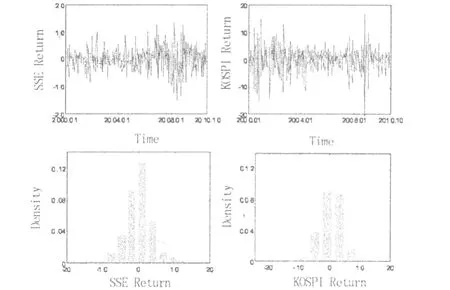
图1中韩股市收益的统计特征

图1直观地展示了SSE与 KOSPI的收益率变化及其分布。在2000年初,KOSPI的波动比较强烈,而后趋缓,与之相反,SSE则于2000年后期波动相对强烈。更为详细、具体的统计特征收录在表1中。中韩股市收益的均值无明显差异,分别为0.12、0.13,但其风险则相差比较明显,SSE的方差为13,而 KOSPI的方差为17。就整体而言,这样的差异与风险要求收益作为补偿的金融理论基本一致。

表1 中韩股票收益率的统计量

(二)平衡性检验

如果时间序列是非平稳,则可能出现伪回归现象。所以在对时间序列建模之前首先要进行平稳性检验,即单位根检验。单位根检验中常使用Augmented Dickey-Fuller(ADF)和 Phillips-Perron(PP)等单位根检验方法,但是每个单位根检验方法都有其局限性,所以本文同时采用ADF和PP单位根检验方法。检验结果见表2。检验结果表明,SSE与 KOSPI在1%的显著性水平下拒绝零假定(H0:存在单位根),表明SSE和 KOSPI收益率为平衡的时间序列。

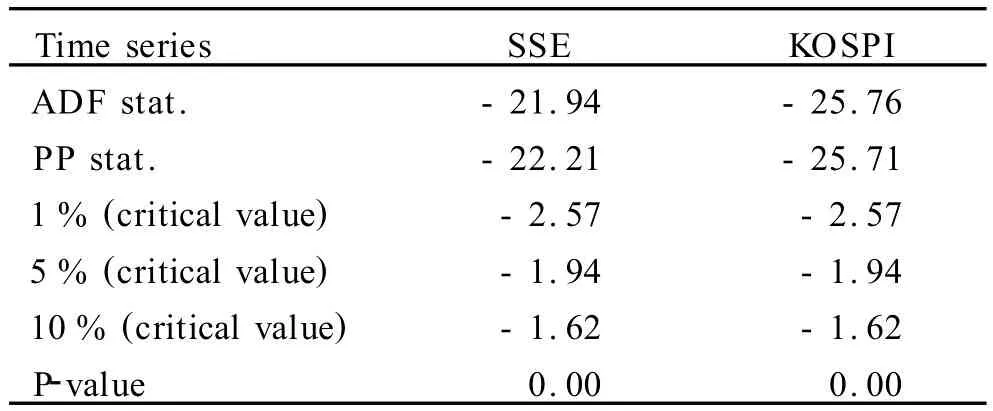
表2 平稳性检验

(三)ARCH 检验

上图1显示SSE与 KOSPI的收益率具有金融序列常有的特征——大幅波动尾随着大幅波动的集聚现象,即ARCH性,更为正规的ARCH检验采用Engel检验方法,检验结果列于表3(见表3)。

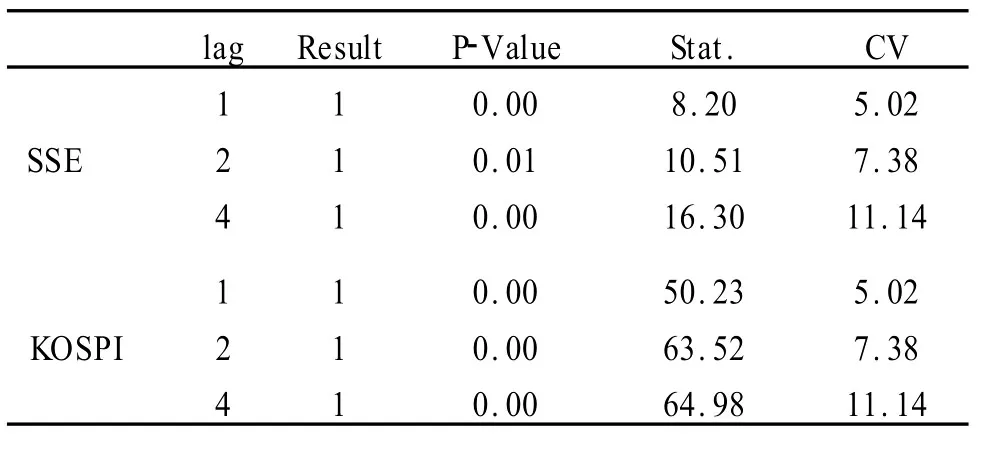
表3 Engel ARCH检验

表3中的第二列(lag)为异方差检验所对应的滞后期,第三列(Result)为拒绝零假设的结果,1代表拒绝零假设,相反0代表不能拒绝零(或称接受零假设),①第四列(P-Value)为 P统计量,即拒绝零假定的概率(显著性水平),第五列(Stat.)为 ARCH检验的统计量,而第六列(CV)为给定显著性水平上的临界值。ARCH检验表明,存在明显的ARCH效应。

(三)参数的估计

在均值方程采用2阶滞后的向量自回归过程,但所有均值方程的系数估计值在统计上不能拒绝零假定,故未在此列出。波动部分及动态相关部分的参数估计及其标准差整理见表4。ω、α、β分别代表各序列的常数项、ARCH参数和 GARCH参数。A和B分别代表DCC方程残差与自回归项的系数。波动部分的参数估计值与均值方程不同,除SSE方程中ARCH参数αSSE外,所有的参数在统计上显著不为零,说明各序列的方差及序列间的相关性有较强的时变及持续性。

表4 波动部分与相关部分的参数估计值

下图2为在上述参数估计值基础上计算出的SSE和 KOSPI间的动态相关关系。由图2可见,SSE与KOSPI收益率的相关系数于样本初期(2000年)就呈下降趋势,这种趋势止于2002年,触底即刻快速反弹,尔后规律性地持续走高,呈V字型。

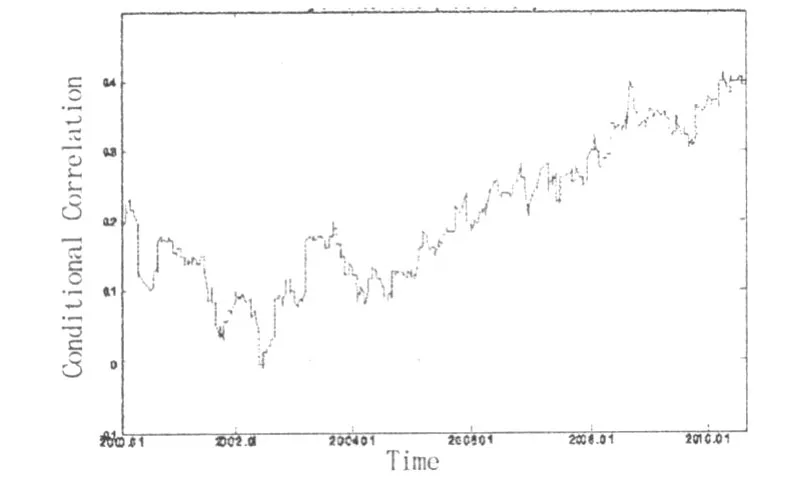
图2基于DCC-GARCH的动态相关关系

(四)实证结果

中韩股市收益的相关性变化趋势可以从国际金融市场一体化的趋势、中国金融市场的日益开发、越发密切的中韩经济交流及1997年亚洲金融风暴对亚洲金融市场的影响中找到大部分答案。

首先,就整体而言,本世纪初全球的金融市场不仅日益融合,而且还有加速之势。各国的金融市场、资本收益的联运性日益上升,此外,中国金融市场的改革开放,使中韩股票市场收益率相关系数长期快速向上攀升。

其次,1997年亚洲金融危机重创了韩国经济,从实物商品到金融领域无不深受其害,股票收益自然是首当其冲。学者对其影响的持续时间说法不一,最保守的意见也是持续到2000年以后。事实上,因金融危机引发的一系列金融、货币改革于2002-2003年才正式完成。从这个视角而言,1997年亚洲年金融危机引发的系列影响于2002-2003年后才完全消除,而这与图2中相关系数变化的转折期相符。反观其对中国经济的影响,其害则远弱于韩国,就金融市场而言,因中国的金融管制严格,更轻于实物经济。

值得关注的一个现象是在2007-2009年美国次贷危机引发的全球金融危机期间,SSE与 KOSPI收益的相关系数并无明显的变化。2007-2009年的全球性金融危机使全球的金融体系受到严重的冲击,唯有中国受到的冲击仍然最小。②但相关关系保持如此稳定的发展说明,这次金融危机对中国与韩国股市的冲击是对称的,这也是中国金融市场与国际金融市场融合程度已经上升到一定程度的标志。中国已经不能像1997年亚洲金融危机爆发时那样“独善其身”了。

五、稳健性分析

在实践中多采用数值优化(Numerical optimization)来估计条件异方差模型的参数,(不好的)参数的初始值可能影响最终估计值的准确性,即可能导致局部优化而不是全局优化,进而影响分析结果及结论的准确性。为了检验DCC-GARCH实证分析结果的稳健性,笔者使用滚动样本无条件相关系数及对角VEC-GARCH模型计算的条件相关系数与之进行比较。

(一)基于滚动样本的相关关系

利用滚动样本求得的相关系数为无条件相关系数,而不是前面分析的条件相关系数,但是当样本适当时,可近似表现相关关系的变迁趋势。下图3为使用25、50、80、100个滚动样本所计算的 SSE与KOSPI收益率相关系数。在这四个滚动样本下,相关系数的变化非常相似,虽然与前文所述的条件相关关系系数相比极为不稳定,但也印证了一些共同的特征,即2002年前相关关系系数是先呈下降趋势,而后是逐渐走高。

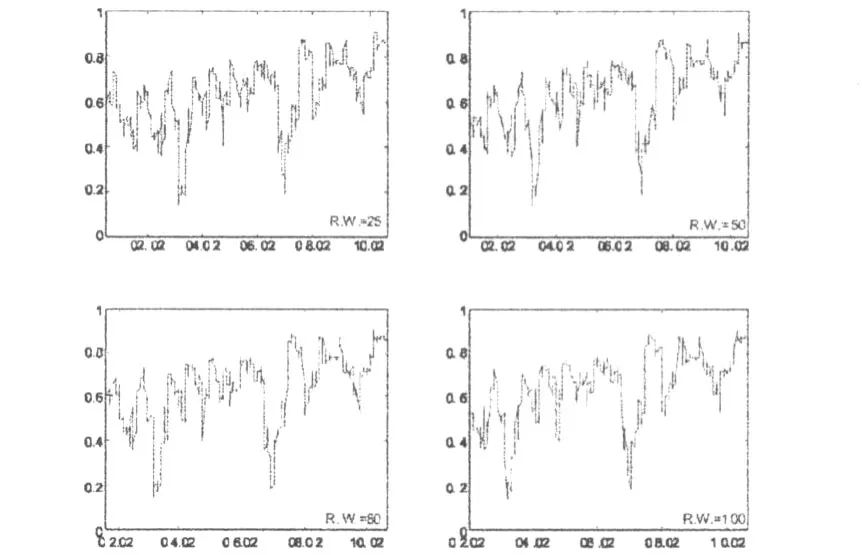
图3基于滚动样本的无条件相关关系

(二)基于对角VEC-GARCH的相关关系

VEC-GARCH也是研究多变量条件异方差问题中常使用的模型之一,为了检验DCC-GARCH模型的结果与结论,本文亦采用相同的均值方程及ARCH结构设定并估计其参数,进而计算相关关系系数。由下图4可见,由VEC-GARCH得出的相关系数与前文采用DCC-GARCH得出的结果非常相似,2002年“冰点”以后,相关系数持续上升,且在2007-2008年全球金融危机期间无显著变化。

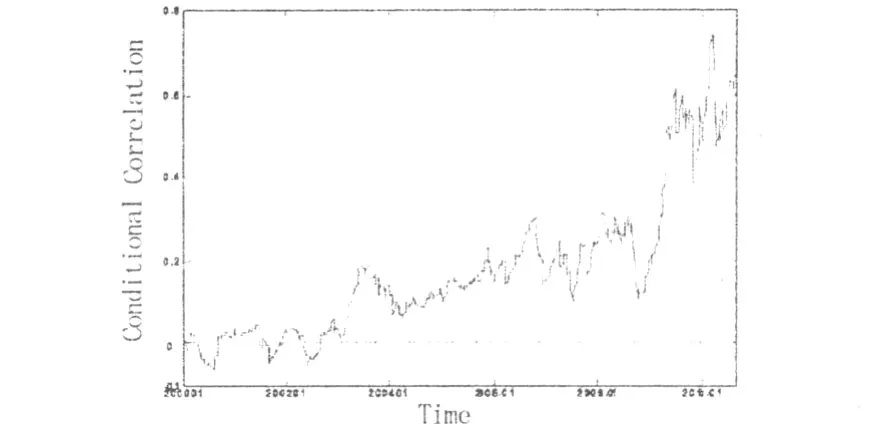
图4基于VEC-GARCH的相关关系

以上的滚动样本无条件相关分析及VECGARCH分析结果表明,基于DCC-GARCH的动态相关关系结论充分值得信赖。

六、结论及建议

本文通过采用DCC-GARCH模型对2000-2010年间的中国与韩国股票市场收益的相关关系进行了实证分析。分析结果表明,中韩两国的股票市场收益间的相关性呈逐年上升趋势,并且上升速度非常快。这表明,1997年亚洲金融危机与2007年美国次贷危机引发的全球金融危机对中韩证券市场相关关系的影响大相径庭:1997年亚洲金融危机的余波使中韩证券市场的相关关系减弱,而2007-2009年全球金融危机期间则无明显下降或上升变化。这种现象更多地源自中国的金融开放与国外证券市场间的融合。

根据本文实证分析的结果,笔者提出以下建议:其一,对中韩两国证券进行组合者而言,应充分注意两国之间日益快速上升的相关性,因组合投资的风险分散能力越来越小,可适当减持一方的份额。其二,鉴于韩国是易受金融危机感染的国家,应加强危机管理机制,当发生金融危机等外部冲击时,可及时向资本流动的齿轮中加入“砂子”,减轻外部资本价格波动对国内股市的传染。最后,适当调整金融开放速度,在金融开放条件下,国内金融机构要平等地直面国际金融冲击,但是抗击金融冲击的能力不仅与经济、金融的基础条件相关,而且也需要应对金融冲击的实践经验,乃至与国际金融机构间的协作能力,这一切都需要时间和(金融)事件来加以强化。

注释:

①Engel ARCH test中的零假设为不存在ARCH效果(no ARCH effects)。

②另有部分学者认为中国是2007-2008年全球金融危机受益者,但无正式的研究成果支持此观点。

[1] Hamao,Y.Masulis,R.W.and V.Ng.Correlations in Price Change and Volatility across International Stock Markets[J].Reviews of Financial Studies,1990,(3):281-307.

[2] Jang,H.and Sul,W.The Asian Financial Crisis and the Co-Movement of Asian Stock Markets[J].Journal of Asian Economics,2002,(13):94-104.

[3] Worthington,A.and Higgs,H.Transmission Of Equity Returns And Volatility In Asian Developed And E-merging Markets:A Multivariate Garch Analysis[J].International Journal of Finance and Economics,2004,9(1):71-80.

[4] Arouri,M.E.H.,Jawadi,F.and Nguyen,D.K.International Stock Return Linkages:Evidence from Latin American Markets[J].European Journal of Economics,Finance and Administrative Sciences 2008,(11):54-65.

[5] 陈守东,韩广哲,荆伟.主要股票市场指数与我国股票市场指数间的协整分析[J].数量经济技术经济研究,2003,(5):124-129.

[6] 徐有俊,王小霞,贾金金.中国股市与国际股市联动性分析——基于DCC-GARCH模型研究[J].经济经纬,2010,(5):124-128.

[7] Engel,R.Dynamic conditional correlation[J].Journal of Business and Economic Statistics,2002,(3):339-350.