具有生物控制的非自治n种群竞争系统的全局吸引性

李玉辉

（北方工业学校数学教研室，辽宁盘锦 124021）

0 引 言

具有重要实际意义的多种群生态系统动力学性质历来受到学术界的重视，现已取得了大量的研究成果[1-5]。在具体的生态问题中，人们为了达到对生态系统的控制，采用了一种有效的办法即是引入反馈控制变量。对于下述反馈控制系统:

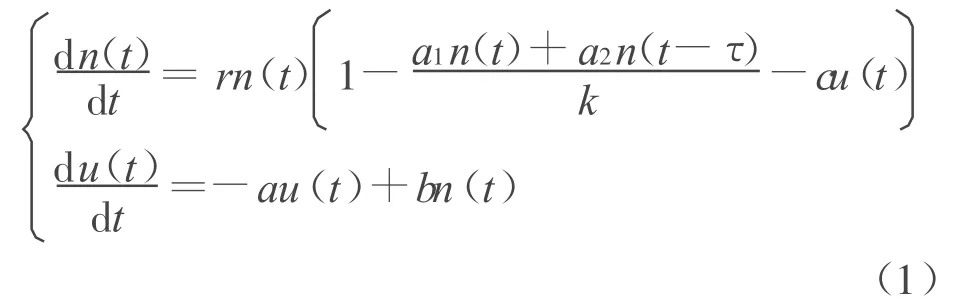
式中:n（t）——t时刻种群的密度;

u（t）——t时刻反馈控制变量。

文献[6-7]研究了该模型正平衡点的稳定性，给出了全局渐近稳定的充分条件。基于以上工作，文中考虑如下具有生物控制的非自治n种群Lotka-Volterra竞争系统:

式中:xi（t） ——第i个相互竞争种群（即食饵种群）在时刻t的密度，i=1，2，…，n;

u（t）——控制变量（即捕食者种群）在时刻t的密度;

aij（t），bi（t），ci（t），di（t），fi（t）（i，j=1，2，…，n）——皆为关于t∈R+=[0，∞）的连续且恒正有界函数。

系统（2）的生态意义是:当n个相互竞争种群的增长率较高时，引入一个捕食者种群实施生物控制，借以实现对系统的整体控制，使人们能够在生态平衡中获益。由于生物控制代表人类的干扰作用，所以研究生态系统（2）的动力学性质更有实际应用价值。

设

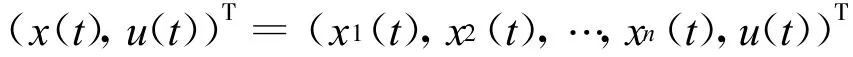
是系统（2）的任意解，初始条件为:

文中记:

式中:g（t）——连续有界函数。

近年来，具有生物控制的生态系统备受关注[8-9]。据悉，至今尚未有学者研究系统（2）满足正初值条件（3）的动力学性质。文中首先运用微分方程中比较原理研究系统的一致持久性，然后通过构造Lyapunov函数得到系统全局渐近稳定的充分条件，最后应用文中定理对实例的动力学行为进行了判定。

1 持久性

定义1 如果存在一个紧区域D⊂Rn+1+，使得系统（2）满足正初值条件（3）的每一解最终进入并保留在区域D，则称系统（2）是一致持久的。

引理1 Rn+1+是系统（2）的正不变集。

证明 系统（2）等价于

可见，当xi（t0）＞0，u（t0）＞0（t0≥0）时，必有xi（t）＞0，u（t）＞0，i=1，2，…，n。证毕。

证明 根据引理1，设（x（t），u（t））T=（x1（t），x2（t），…，xn（t），u（t））T是系统（2）满足正初值条件（3）的任意解，由系统（2）的第一式有

由比较定理知，存在T1＞0，Mi≥M*i，当t＞T1时，恒有xi（t）≤Mi，i=1，2，…，n。

当t＞T1时，由系统（2）的第二式有

同样地，存在T2＞T1，R≥R*，当t＞T2时，恒有u（t）≤R。

当t＞T2时，由系统（2）的第一式有

由比较定理知，存在T3＞T2，m*i≥mi＞0，当t＞T3时，恒有xi（t）≥mi，i=1，2，…，n。

当t＞T3时，由系统（2）的第二式有

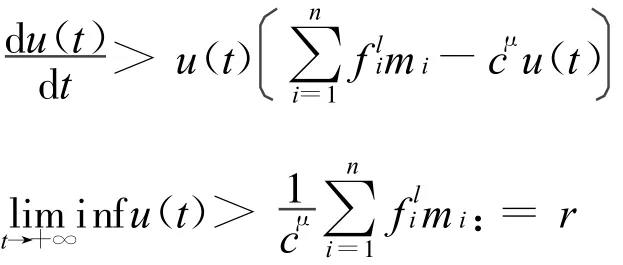
可知，存在T＞T3，r*≥r＞0，当t＞T时，恒有u（t）≥r。

综上，当t＞T时，恒有

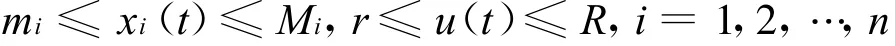
据此，获得紧集

是系统（2）的正向不变集和最终有界区域。证毕。

2 全局吸引性

定义 2 设系统（2）的一个正解为（y（t），v（t））T，任意正解为（x（t），u（t））T，如果

则称系统（2）是全局吸引的。

定理2 设系统（2）满足正初值条件（2）和定理1条件，如果

证明 设系统（2）的一个正解为（y（t），v（t））T，任意正解为（x（t），u（t））T由定理1条件知，当t＞T时，恒有mi≤xi（t），yi（t）≤Mi，r≤u（t），v（t）≤R，i=1，2，…，n。构造Lyapunov泛函

沿着系统（2）的解直接计算Vi（t）的右上导数，得到

取Lyapunov泛函

沿着系统（2）的解直接计算W（t）的右上导数，可得

再构造Lyapunov泛函

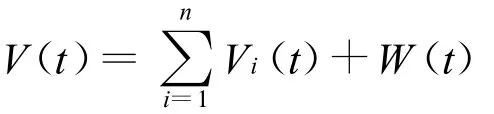
沿着系统（2）的解估计V（t）的右上导数，获得

据此，从T到t积分得

从而

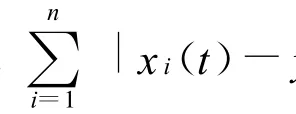
由引理2知

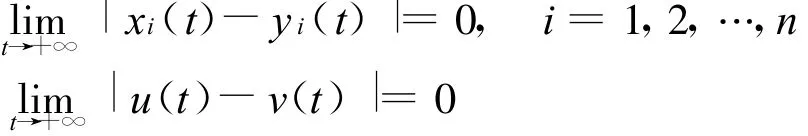
即

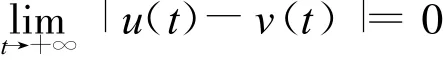
故系统（2）正解（y（t），v（t））T是全局吸引的。证毕。

3 应用举例

根据系统（2），考虑如下具有生物控制的非自治两种群Lotka-Volterra竞争系统:

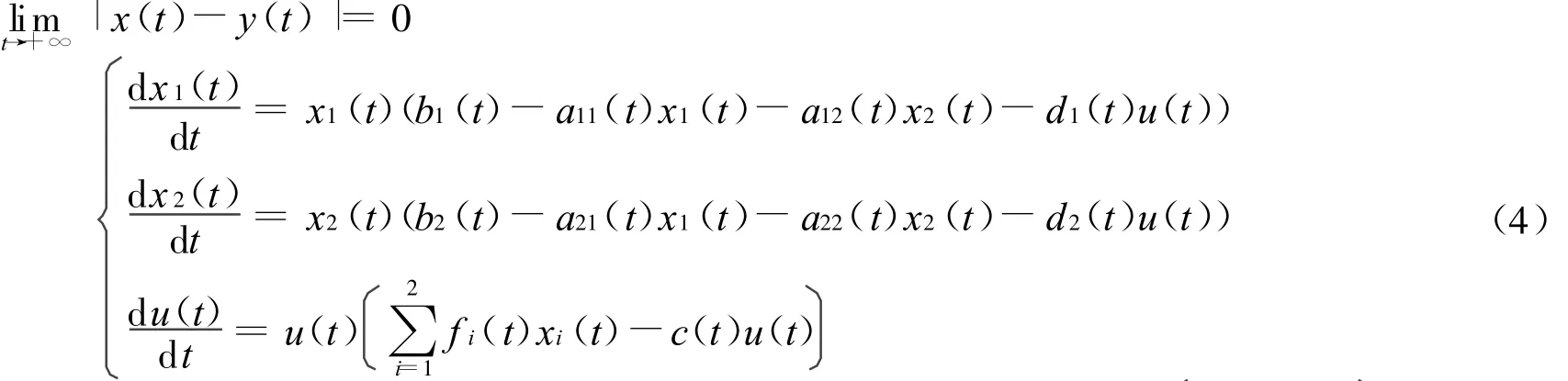
其中

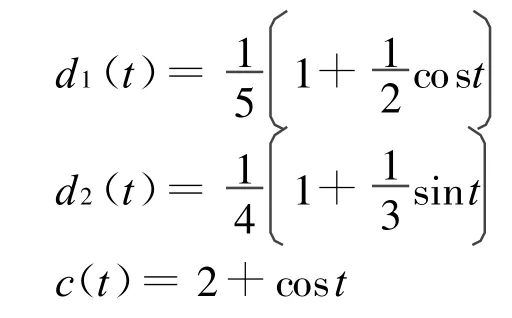
于是，有

经计算，得到

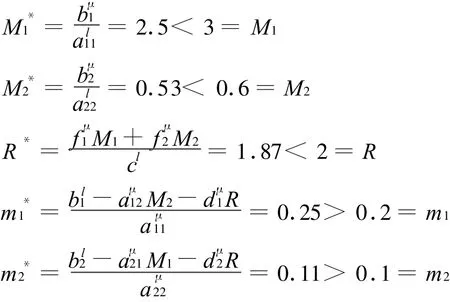
则由定理1知，系统（4）是一致持久的。

由于

故由定理2知，系统（4）是全局吸引的。

[1] 陈兰荪，陈键.非线性生物动力系统[M].北京:科学出版社，1993:102-130.

[2] Ruan S，Xiao D.Global analysis in the predatorprey system with non-monotonic functional response[J].SIAM J.Appl.Math.，2001，61（1）: 1445-1472.

[3] 程荣福，常亮.具无限时滞和非单调功能性反应捕食系统的多周期解[J].吉林大学学报:理学版，2010，48（5）:761-765.

[4] 张正球，王志成.基于比率的三种群捕食者-食饵扩散系统的周期解[J].数学学报，2004，47（3）:531-540.

[5] 黄玉梅.具HollingⅡ型功能反应的时滞扩散模型的全局稳定性[J].生物数学学报，2006，21（3）:370-376.

[6] Gopalsamy K.Stability and oscillations in delay differential equation of population dynamics[M].Boston:Kluwer Academic Publishers，1992.

[7] Gopalsamy K，Weng Pei-xuan.Feedback regulation of logistic growth[J].Internat J Math.and Math. Sci.，1993，16:177-192.

[8] 程荣福，孙吉荣.具生物控制的时滞阶段结构种群模型的稳定性[J].北华大学学报:自然科学版，2008，9（2）:97-103.

[9] 程荣福.一类具生物控制的多滞量捕食模型正周期解的存在性[J].北华大学学报:自然科学版，2010，11（1）:1-6.

[10] Barbalat I.System dequation differentilles doscilltion nonlinears[J].Rev.Math.Pure.Appl.，1959（4）:267-270.