二部竞赛图中的最长圈问题
雷万鹏, 刘凌晨, 韩 静
(山西大学商务学院理学系,山西太原 030051)
0 引 言
文中所使用的术语和记号与文献[1]一致。
设T(X,Y,A)为一个 p×q阶二部竞赛图,(X,Y)是T(p,q)的一个划分,令|X|=p,|Y|= q。分别用d+T(v)和d-T(v)表示v在图T中的出度和入度。
如果T(p,q)满足条件:uv∉E且存在点w,使得uw∈E,wv∈E⇒d-(u)+d+(v)≥k,则称T(p,q)满足L(k)条件。
如果T(p,q)满足条件:uv∉E,d+(u)+ d-(v)≥k,则称T(p,q)满足O(k)条件。利用条件O(n)[2],Jackson[3]证明了以下关于二部竞赛图中最长圈的问题。
定理1[3]如果T(p,q)满足O(n)且强连通,则T包含一条长至少2n的圈。
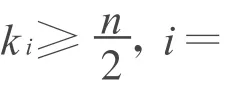
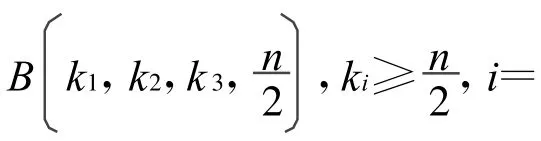
进一步引入定义,设v∈V(T),S⊆V(T),定义
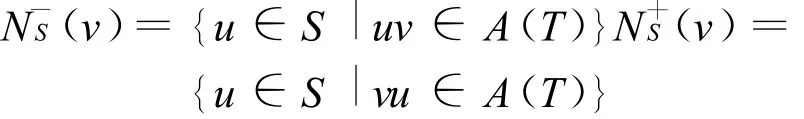
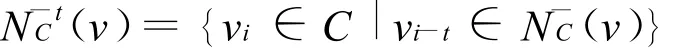
以及
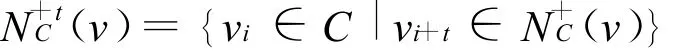
对于所有x∈X1,y∈Y,若X1∈X,Y1∈Y,且xy∈A(T),则将其写为 X1⇒Y1,反之亦然。如果X1={x},那么可改为x⇒Y1。对于u,v∈V(T),u~v表明(u)=(v)且(u)=(v)。
1 主要结论
在证明结果以前先证明一个推论。
推论1 令C=v1v2…v2kv1为二部竞赛图T中一条最长圈,且P=u0u1…um为T-C中的一条路。
1)如果T是强连通的,那么T-C中无圈[4];

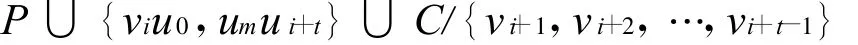
比C长,故矛盾。
则有vi-1u0,umvj+1∈A(T),不失一般性,假定j>i。令

则vsu0,u0vs+2∈A(T)。进而由3)得到vs+1um∈A(T)。因此,很容易发现C′=v1…vi-1u0vs+2vjvi…vs+1umvj+1…v1是一个比C长的圈,矛盾。
证明5):考察路P′=u0u1…um-1。因为m≥2且为偶数,那么m-1≥1且m-1为奇数,结合(um)⊆(um-1)和4),5)的结论成立。


利用这个等式和推论1中的2),得到
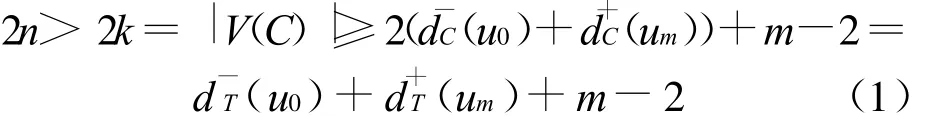
另一方面,我们观察u0和um两点。
情形1 假设m=1,则P=u0u1。我们知道u0u1∉A(T),如果存在一个点w∈T满足u1w∈A(T),wu0∈A(T)。则有(u1)+(u0)≥n。然而,我们知道如果u0u1∈A(T),那么u0,u1,不会同时属于X或Y。不失一般性,我们假设u0∈X,u1∈Y。由上述假设有 u1w∈A(T),wu0∈A(T)。由此可见,w既不属于X,又不属于Y,这与T是一个二部竞赛图矛盾。故当m=1时,不存在w∈T,使得u1w∈A(T),wu0∈A(T),即m =1时,不满足条件L(n)。
情形2 当m≥2时,可以发现 u0um∉A(T),假设对于任一个m,都存在一个点,使其u0um满足条件L(n),则得到

结合式(1)和式(2),解不等式得m≤2且|V(C)| =2n,即m=2。
当m=2时,P=u0u1u2,故至少存在一点u1,使其满足条件L(n)。故只考虑当m=2时的情况即可。
论断1[6-7]当viu0∈A(T)时,1≤i≤2n,u0⇒{vi-2,vi+2}。

即
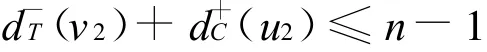
论断2[6]当u2vi∈A(T)时,1≤i≤2n,{vi-2,vi+2)⇒u2。
将每条弧的方向颠倒并结合论断1很容易得到。
结合推论1中的3)以及论断1和诊断2,可以得到结论,当n为偶数且不失一般性,将T中顶点以下列方式重排:
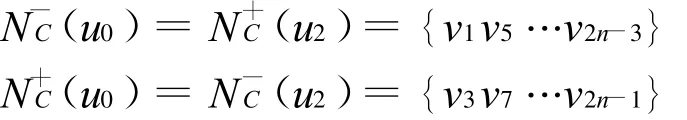
由推论1中的3)得到
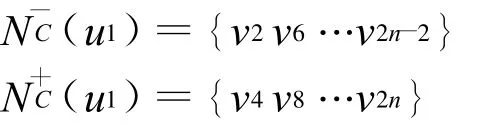
论断3
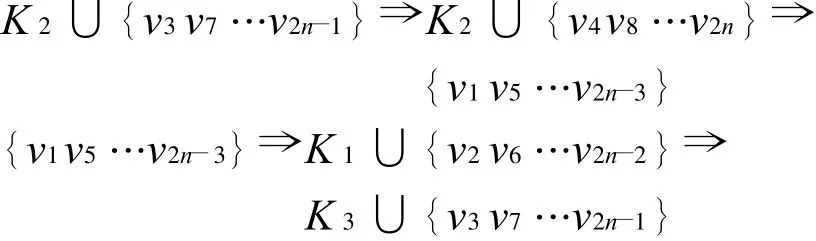
设圈
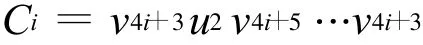
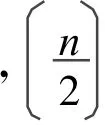
因此
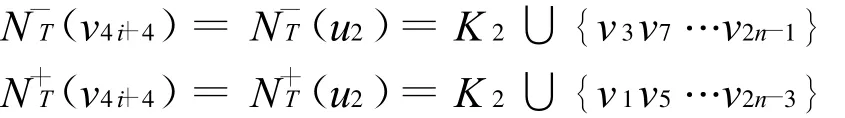
另外,我们很容易发现对uK3∈K3有uK3~u2。故

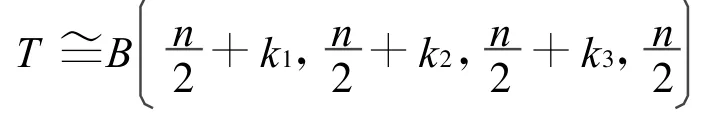
定理证毕。


[1] J A Bondy,U S R Murty.Graph theory with applications[M].New York:Macmillan,1976.
[2] Wang Jianzhong.On arc even pancyclicty in diregular bipartite tournaments[J].Kexue Tongbao,1987,1:76.
[3] B Jackson.Long paths and cycles in oriented graphs [J].J.Graph Theory,1981,5(2):149-157.
[4] Y Manoussakis.Extremal problems in directed graphs[D]:[Ph D Thesis].[S.l.]:University Parix-XI,1987.
[5] J Ayel.Degrees and longest paths in bipartite digraphs[J].Ann.Discrete Math.,1983,17:33-38.
[6] D Amar,Y Manoussakis.Cycles and paths of many lengths in bipartite digraphs[J].J.Combin.Theory Ser.B,1990,50:254-264.
[7] R Haggkvist,Y M anoussakis.Cycles and paths in bipartite tournaments with spanning configurations [J].Combinatiorica,1989,9(1):51-56.

