一种基于最大最小特征值的协同频谱检测算法
康安康, 何 斌
(1.秦皇岛91404部队,河北秦皇岛 066000; 2.中国科学院长春光学精密机械与物理研究所,吉林长春 130033)
0 引 言
随着从单一的语音通信向无线多媒体以及Web类型应用的转变,对更高数据率的需求正不断增加。然而,目前留给新系统、业务和技术的频谱非常少,甚至没有频谱可以分配。可用频谱的匮乏已经成为制约无线通信新技术发展的最大障碍。
认知无线电作为一个解决频谱拥挤问题的尝试而出现。自1999年瑞典的Jeseph Mitola[1]博士提出认知无线电的概念以来,认知无线电迅速成为无线通信领域的研究热点。认知无线电技术成为解决目前频谱资源紧张的有效手段。
当前许多新的单节点频谱感知方法陆续被提出。文献[2]提出了一种宽带多步频谱检测方法,该方法将整个的频谱检测工作分为两步进行,即粗检测方法和细检测方法;文献[3]提出了一些基于GLRT(广义似然比检验)的有效频谱感知方法。单节点的最大最小特征值检测法[4-5](Maximum and Minimum Eigenvalue,MME)是由新加坡电信研究院提出的。这种算法同能量检测一样具有复杂度低,不需要先验信息的优点,同时还能克服噪声不确定性的影响。文中在分析了上述方法的基础上,提出了一种基于最大最小特征值加权的协同频谱感知算法。该算法保持了单节点MME算法的优点,并且进一步提高了检测概率。
1 系统模型
在基本的发射机端检测中,系统模型[6]如下:

1)H0:接收信号只存在噪声(没有发射信号);
2)H1:接收信号中同时存在信号和噪声。
式中:ηi——噪声,这里假设N个样点上叠加的都是独立同分布的高斯白噪声,且ηi~N(0,σ2);
xi——授权用户信号的第i个样点,表示认知用户检测到的第i个信号;
h——信道增益。
对于各参与感知的节点,假设信号是数字调制并且为过采样的。设s(n)为数字调制的源信号,并且定义其符号周期为T0,通过滤波和传输信道得到的信号为:

其中,h(t)由发射滤波、信道响应和接收滤波共同作用形成。假设h(t)具有有限支撑[0,Tu]。假设接收信号为过采样的,并且过采样因子为M,即采样周期为:

定义:

式中:n=0,1,…;i=1,2,…,M。
可以得到:

式中:N=Tu/T0。
则构成采样矩阵表达式为:
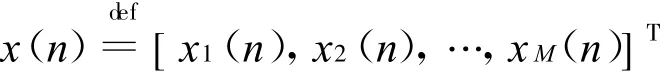
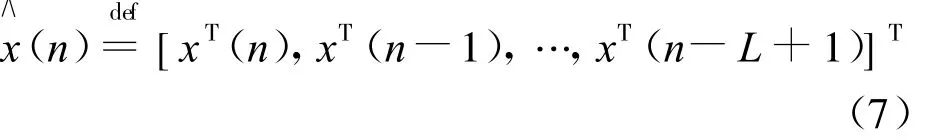
即:

2 加权系数的选择
采用数据融合方法中的软判决算法,对各单节点检测的最大最小特征值进行加权与判别阙值进行比较,从而判断信号的存在性。因此,加权系数的选择成为重点。
2.1 信号因素
电磁波在自由空间内传播发生的能量损耗,考虑到天线辐射的方向性、接收与发射天线的极化特性匹配情况等因素,假定接收天线处于最佳接收状态下,在距离发射天线d处,接收天线的接收功率[7]表示为:

式中:Pt——发射功率;
Gt——发射天线增益;
Gr——接收天线增益;
λ——电磁波波长,m;
d——接收机与发射机之间的距离。
自由空间中,信号从发射机到接收机只沿一条路径传播。现实环境中,特别对于移动通信传播环境,由于传播路径上存在各种不同类型和尺寸的地物,这些地物对电磁波的反射、散射和吸收是普遍存在的,因此,无线电波传播的功率衰减比自由空间中的速率 d-2快得多,在室外一般取d-4。
2.2 噪声因素
传感器网络中,有一种最优加权方法[8],它的原理是基于能量检测的,因此在频谱检测中也同样适用,其推导的估计表达式的均方误差为:

3 算法实现
通过第2节的分析可以得出以下结论,从信号和噪声方面考虑,加权系数可以用主用户与子节点之间的距离d和噪声功率来表示,距离衰减通常采用d-4,因此,文中采用d-4来表示信号功率因素。
加权系数表示为:

式中:di——子节点i到主用户的距离;
由以上分析可以得出特征值比值融合的CMME算法实现步骤如下:
1)各子节点进行L点信号采样并发送至主节点,构成采样数据矩阵;
2)记R(NS)为收到信号的样本协方差矩阵,根据步骤1)的采样数据矩阵计算得出协方差矩阵:

3)计算协方差矩阵R(NS)的最大最小特征值比值θi;
4)根据

计算判别阙值γ;
5)各子节点将计算所得的最大最小特征值比值θi发送至主节点;主节点按照各子节点加权系数计算加权后的特征值比值,计算方法如下:

式中:n——子节点总数;
6)按照下面规则判决:

式中:H0,H1——分别为信号不存在和信号存在的情况。
4 仿真与分析
仿真了节点采样点数为1 000和2 000的情况下,最大最小特征值比值融合的协同频谱感知方法的检测概率随信噪比变化的曲线,分别如图1和图2所示。
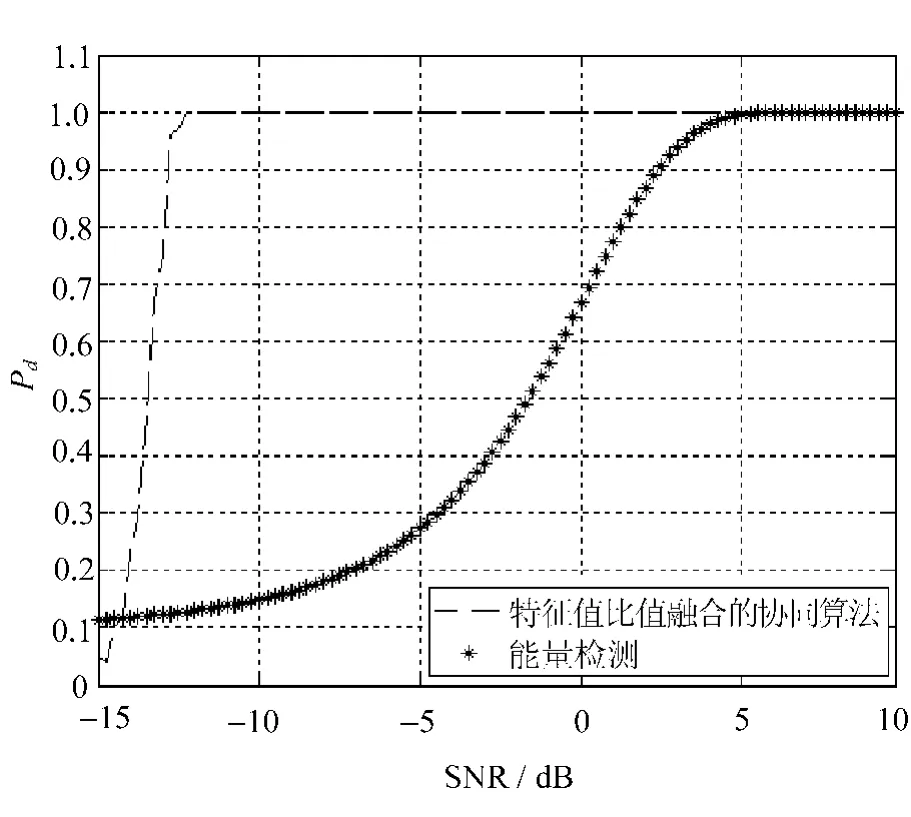
图1 采样点数为1 000的CMME算法性能仿真图
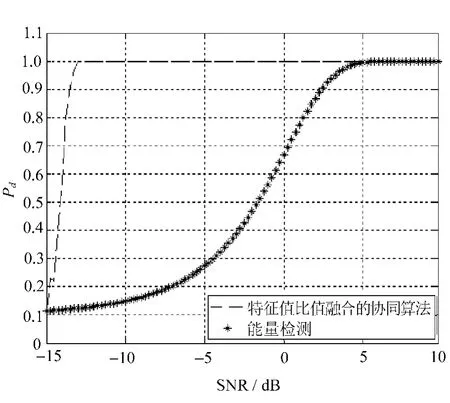
图2 采样点数为2 000的CMME算法性能仿真图
仿真环境设定各子节点虚警概率为0.10,能量检测虚警概率也为0.10,信噪比范围是-15~9.75 dB。
从图中可以看出,能量检测在信噪比达到5 dB以后,检测概率才达到100%,而采样点数分别为1 000和2 000的最大最小特征值比值融合方法的检测概率在-12 dB以下时,即开始收敛至100%,其中,采样点数为1 000的曲线比采样点数为2 000的曲线更快地收敛到1。
在和能量检测对比情况上(见图2),两条曲线都收敛于1之前,采样点数为2 000的最大最小特征值比值融合的感知方法的仿真曲线一直在能量检测曲线之上,即其检测效果要远远好于能量检测。图1中所示的两条曲线中,在低信噪比情况下,采样点数为1 000的最大最小特征值比值融合的感知方法仿真曲线有一小段在能量检测之下,其检测效果比能量检测的效果要差,这也说明了各子节点的采样点数Ns对最大最小特征值比值融合的感知方法有着很大的影响,当采样点数越多时,信号检测概率也就越大。
下面从接收机操作特性曲线(ROC)方面比较新算法与能量检测算法的优劣。接收机操作特性曲线是在一定的信噪比情况下,虚警概率与检测概率的关系曲线,文中的新算法ROC曲线是在SNR=-15 dB的情况下得到的,能量检测算法是在SNR=-3 dB情况下得到的。3个检测节点的SNR值都为-15 dB的情况下,特征值比值融合的协同感知方法与能量检测算法比较如图3所示。

图3 接收机操作特性曲线
图中,基于特征值比值融合的协作频谱感知算法的不同检测概率和虚警概率是通过改变γ因子得到的,而能量检测算法不同的虚警概率和检测概率是通过改变单节点的能量检测的判决门限值得到的。从图中可以看出,在一定的虚警概率下,文中提出的检测算法的检测概率要高于能量检测的检测概率,检测性能比能量检测算法有很大的提高。
5 结 语
提出了一种基于最大最小特征值比值融合的协同检测算法,该算法继承了单节点最大最小特征值算法不需要先验信息,同时还能克服噪声不确定性影响的优点,也进一步提高了检测概率。仿真证明,该算法与能量算法相比具有很大的优越性。
[1] Rieser C J.Biologically inspired cognitive radio engine model utilizing distributed genetic algorithms for secure and robust wireless communications and networking[D]:[Ph D Thesis].Augest:Virginia Tech,Blacksburg,VA,2004.
[2] Lim T J,Zhang R,Liang Y C,et al.GLRT-based spectrum sensing for cognitive radio[C]//IEEE GlobeCom.New Orleans,USA:[s.n.],2008.
[3] 朱江.频谱感知算法及授权用户用频行为研究[D]: [硕士学位论文].武汉:华中科技大学,2010.
[4] Zeng Y H,Liang Y C.Maximum-minimum eigenvalue detection for cognitive radio[C]//The 18th IEEE Intern.Symposium on Personal,Indoor and Mobile Radio Communication Proceedings.Athens Greece:[s.n.],2007.
[5] Zeng Y H,Liang Y C.Eigenvalue based spectrum sensing algorithms for cognitive radio[C]//IEEE Institute for Info Comm Research.November:[s.n.],2009.
[6] 石磊.认知无线电中空闲频谱检测技术的研究[D]: [硕士学位论文].哈尔滨:哈尔滨工业大学,2010.
[7] 周文安.无线通信原理与应用[M].北京:电子工业出版社,2006.
[8] 景博,孙勇.基于集中式最优加权算法的多传感器数据融合[J].电子测量与仪器学报,2004(s4): 1143-1147.

