二阶串联谐振系统Matlab/Simulink仿真

陈 雪

（太原师范学院物理系，山西太原 030031）

0 引 言

信号与系统分析在电子与信息领域中占据着重要的地位[1-2]。传统的理论分析方法是通过数学方法建立方程求解而得出分析结果，需要大量的数学运算。而在现代工程中，随着计算机技术和仿真软件的发展，人们通常利用仿真技术建立数学模型，对实际系统进行模拟，分析不同的信号输入和系统参数改变时系统响应或性能的变化[3]。Simulink作为Matlab的工具箱之一，是交互式动态系统建模、仿真和分析的图形环境，在信号处理领域得到了广泛应用[4-8]。

文中以RLC二阶串联谐振系统为例，利用Simulink动态仿真软件建立了电路形式和框图形式的两种仿真模型，而这两种模型，都可以直观方便地显示系统回路的电流响应曲线。通过模拟仿真可以看到，将Matlab运用到信号与系统的分析中，不但简化了大量的数学运算，而且使系统分析更为简便高效。

1 二阶串联谐振系统的建模

RLC二阶串联谐振系统是连续系统分析的典型研究对象，理论上经常讨论此系统有关回路电流i（t）为响应的问题。文中选取电路参数L= 1 H，C=1 F，用ω=1 rad/s的正弦信号作为激励e（t），首先建立系统的数学模型。根据基尔霍夫电压定律，可建立回路方程

方程左右两边分别求导，得

对上述方程左右两边进行拉式变换，并求得系统函数

其中，极点位置是

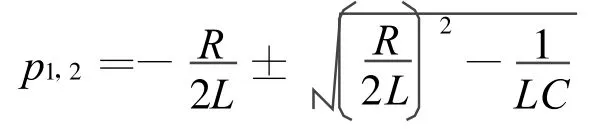
2 基于Simulink的二阶串联谐振系统仿真分析

2.1 电路模型仿真

运用Simulink可以建立二阶串联谐振系统的电路模型，如图1所示。

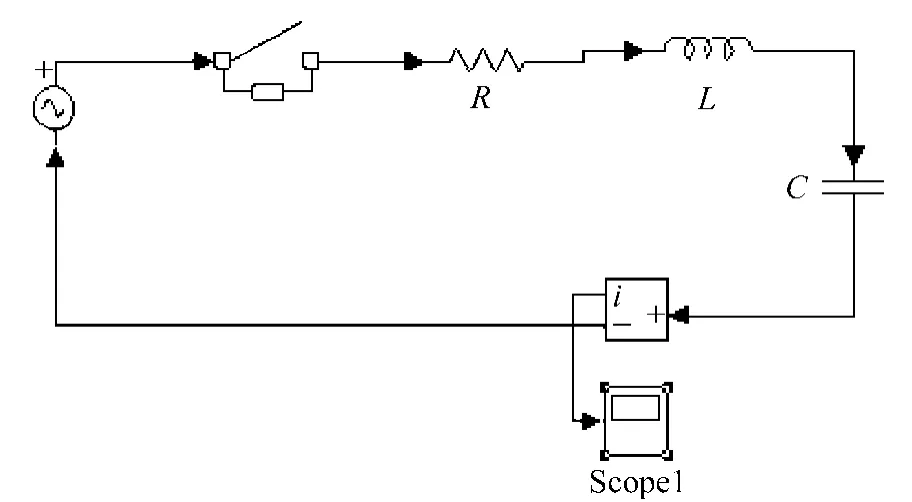
图1 基于Simulink的二阶串联谐振系统电路模型

模型中用ω=1 rad/s的正弦信号作为激励，通过改变电阻的阻值可以改变衰减因子α的取值，从而可以直观地观察不同损耗时的系统i（t）波形。

RLC无损系统（α=0）的i（t）波形如图2所示。

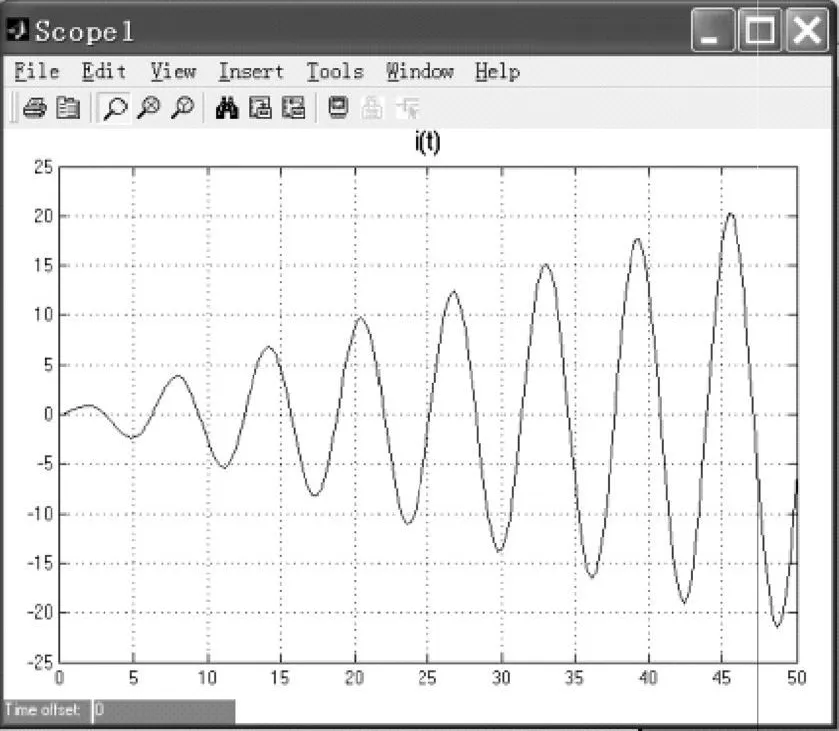
图2 α=0时无损电路正弦激励电流响应

由图可见，由于电路发生了谐振，它的包络为线性增长的同频正弦信号。

另外，通过改变衰减因子α的值，可以更直观地去研究系统正弦稳态过渡过程。同信号激励RLC有损系统（α=0.25，α=1）的i（t）波形如图3和图4所示。

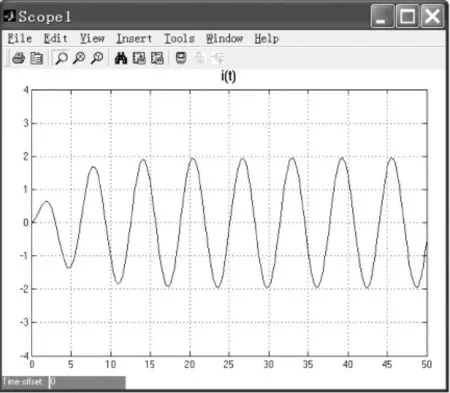
图3 α=0.25时有损电路正弦激励电流响应

图4 α=1时有损电路正弦激励电流响应

可见随着t的增大，i（t）中的暂态响应迅速结束，电路很快进入正弦稳态。

2.2 系统模型仿真

为了对线性时不变（LT I）系统进行分析，需要首先建立与系统相对应的系统函数。以α=1的二阶串联谐振系统为例，取电路参数L=1 H，C=1 F，R=2 Ω，建模后其系统函数可以表示为:

根据梅森公式，上式的分子可以看作是1条前向通路的增益，分母可以看作是2个回路组成的特征行列式，而且各回路都互相接触，由此可以构建系统模型。在Matlab/Simulink运行环境中选择相应的模块，在model板上构建出系统模型，设置相应的参数进行仿真，用直接型和级联型实现的二阶串联谐振系统模型分别如图5和图6所示。

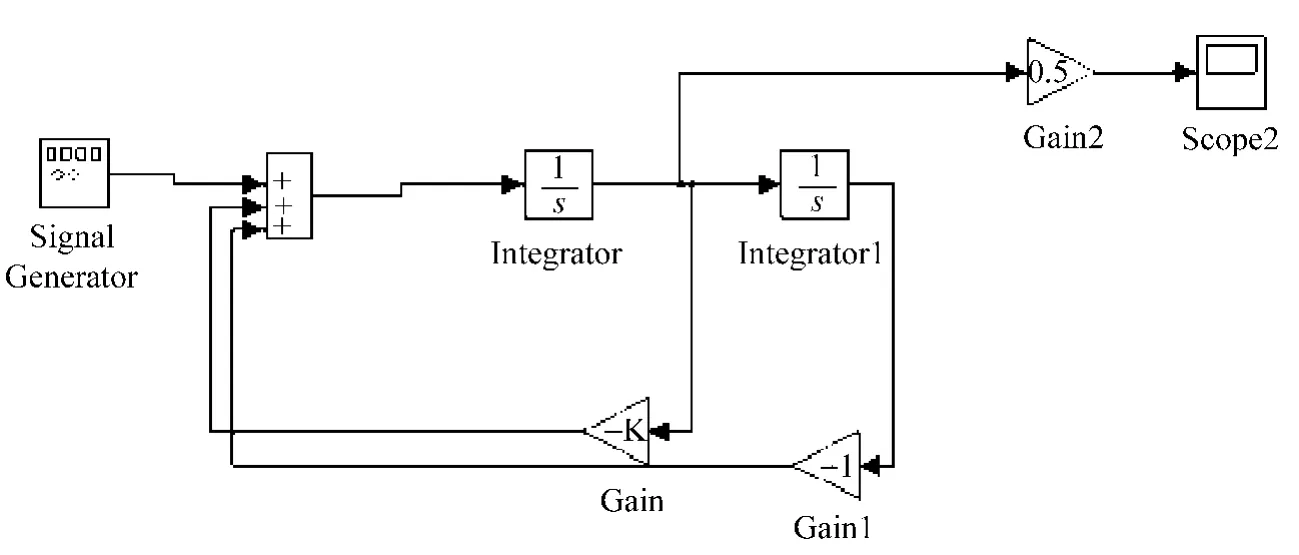
图5 基于Simulink的直接型二阶串联谐振系统模型

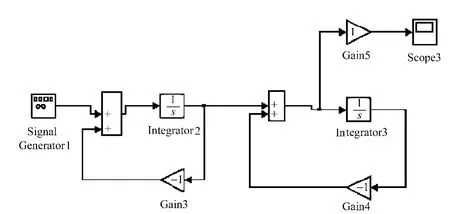
图6 基于Simulink的级联型二阶串联谐振系统模型

双击示波器scope显示正弦激励信号的电流响应结果如图7所示。

通过与图4比较发现，利用系统函数建立的系统模型与实际的电路仿真得到的响应是一致的，体现了利用Simulink进行二阶串联谐振系统建模的准确性。

3 结 语

以RLC二阶串联谐振系统为例，分析了线性时不变系统的建模方法。并利用Simulink动态仿真软件建立了电路形式和框图形式的两种仿真模型，而这两种模型都可以直观方便地显示系统回路的电流响应曲线。通过模拟仿真可以看到，将Matlab运用到信号与系统的分析中，不但简化了大量的数学运算，而且使系统分析更为简便高效，对理论研究和工程应用都具有重要意义。

[1] 郑君里，应启珩.信号与系统[M].2版.北京:高等教育出版社，2004.

[2] 吴大正.信号与线性系统分析[M].3版.北京:高等教育出版社，2003.

[3] 姚俊.Simulink建模与仿真[M].西安:西安电子科技大学出版社，2005.

[4] 谢守清.基于Simulink的“信号与系统”课程教学方法探索[J].宁波工程学院学报，2007，19（4）:100-102.

[5] 张猛，王晓峰.信号与系统建模与仿真[J].长春大学学报:自然科学版，2010，20（8）:63-65.

[6] 党华丽.M atlab/Simulink仿真在信号与系统分析中的应用[J].信息技术，2010（3）:126-127.

[7] 李涛.Simulink仿真在《电路分析》课程教学中的应用[J].中国科教创新导刊，2010（2）:98-99.

[8] 李露，史振威，周付根.基于Matlab/Simulink的幅度调制与解调综合实验设计[J].实验室研究与探索，2011，30（1）:96-99.