基于MATLAB的平面五连杆机构的运动学分析
王锡霖, 严日明, 李 举, 许文艺
(中国地质大学(武汉)机械与电子信息学院,湖北武汉 430074)
0 引 言
连杆机构的应用十分广泛,在生产机械中应用连杆机构可以转变原动机的运动形式,如插齿机中的曲柄滑块机构,在蜘蛛仿生机械中的蜘蛛脚也是连杆机构,还有诸如工业应用中的机械手的传动机构,人造卫星的展开机构、人体假肢等都有广泛应用。对平面连杆机构的运动分析方法有矢量方程图解法和解析法等,其中解析法又分为复数矢量法和矩阵法。矩阵法可以方便地运用标准计算程序或方程求解器等软件包来求解,这里只介绍矩阵法[1]。
1 五连杆机构运动的的数学模型
五连杆机构的结构简图如图1所示。
其中AB长为l1,与固定机架AE的夹角为;BC长为l2,与水平方向的夹角为;CD长为,与水平方向夹角为;DE长为;EF长为与水平方向夹角为;FA长为;机架AE长为。杆件BF为原动件,角速度为,做等角速度运动。

图1 五连杆机构的结构简图
1.1 位置分析
由于有五个杆,因而需要有两个封闭式方程来表示该机构的数学模型[1]。由封闭形ABCDEA与AEFA得到的封闭矢量方程式为:

即

写成两个坐标方向上的投影式,得到该机构的位置方程:

1.2 角速度分析[2]
用1.1中得到的位置方程对时间求一次导数,可得:

1.3 加速度分析
用1.2中得到的角速度方程式再求一次导数,得:
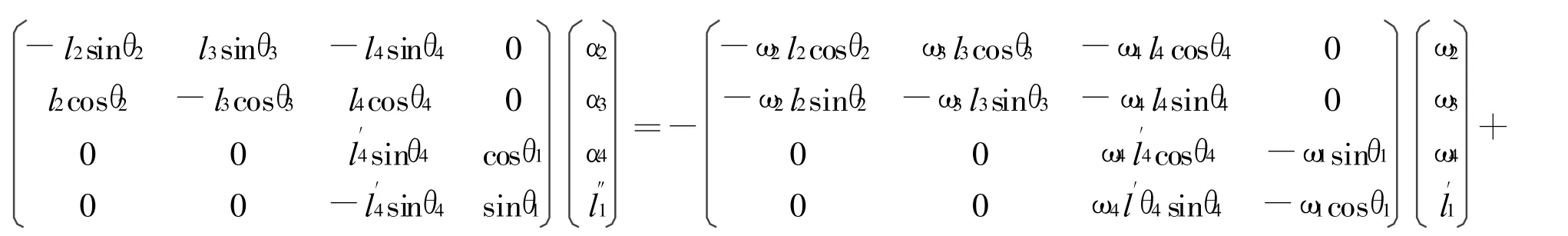

2 三角函数非线性超越方程的解法
前面得到的三组方程都是关于三角函数的非线性超越方程,求解的方法有多种,这里用牛顿-辛普森方法来求解。牛顿-辛普森方法是一种迭代法,它从某一个给定的初始向量开始不断地给以增量直到足够接近精确解。迭代增量是通过非线性方程的级数展开式计算求得,接近精确解的程度就由数值精度要求来确定。求解过程中要用到非线性方程的雅克比矩阵J[3-4]。
在MATLAB函数编写中用到了while条件循环语句,编写了名为rrrposi的M函数,可以求解1.1中的位置函数,再利用for循环语句得到随原动件BF运动其它构件的位置图像[5-8]。
rrrposi函数程序[5]如下:

接下来在MAT LAB命令窗口中运行如下程序,就可以得到BF连续运动时各个构件的位置:


表1 P矩阵
同样利用这个步骤中求得的各个未知数的解,再利用牛顿-辛普森方法对角速度方程组进行求解,之后再对加速度方程组进行求解。
3 输出图像
输出各个杆的角位置图像,程序如下:
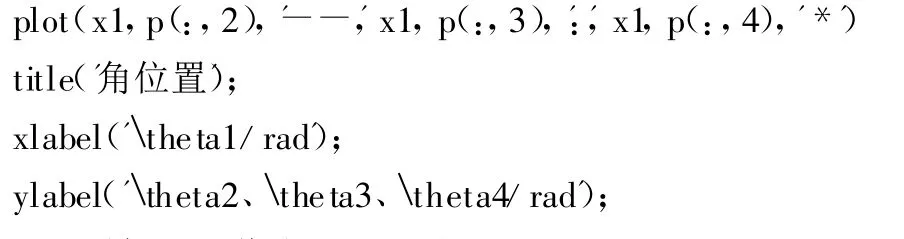
输出图像如图2所示。
用相同的方法输出杆AF长度的变化图像如图3所示。
输出各个杆的角速度图像如图4所示。
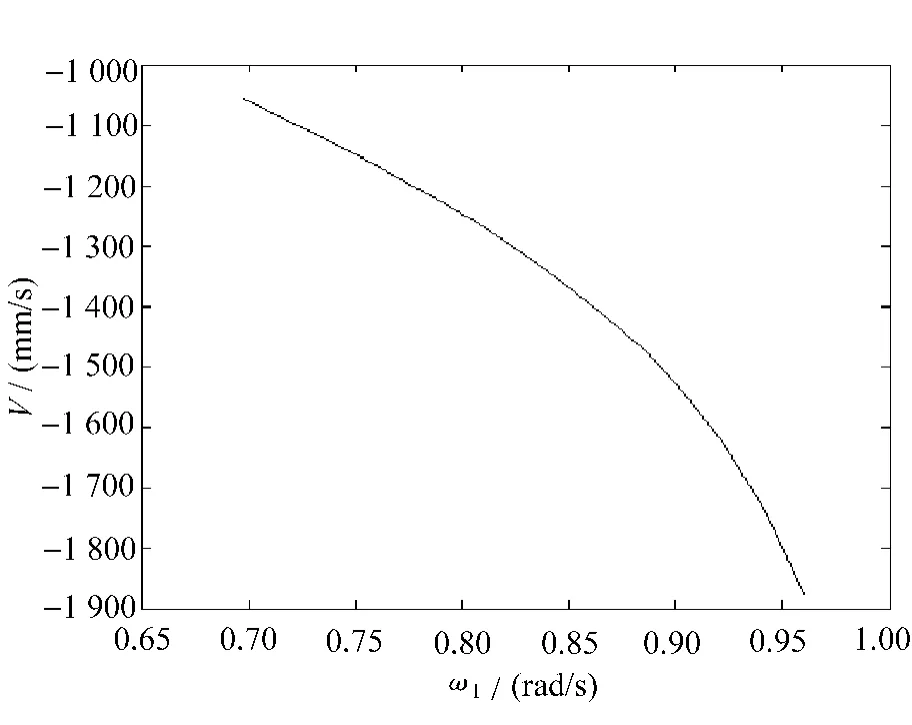
图2 角位置图像

图3 AF长度的变化图像

图4 各杆角速度图像
滑块速度图像如图5所示。
各个杆的角加速度图像如图6所示。
滑块的加速度图像如图7所示。

图5 滑块速度图像

图6 角加速度图像

图7 滑块运动加速度
4 结 语
对平面正弦连杆机构进行动力分析,并且依据其数学模型运用MAT LAB编程,绘制出了曲柄在连续360°的运动过程中各个运动副变化规律及平衡力偶的变化规律曲线图,使得设计过程中力与位置的关系直观易懂,对实际设计有一定指导意义。
[1] 孙恒,陈作模,葛文杰.机械原理[M].北京:高等教育出版社,2006.
[2] 同济大学数学系.线性代数[M].北京:高等教育出版社,2009.
[3] 曲秀全.基于MAT LAB/Simulink平面连杆机构的动态仿真[M].哈尔滨:哈尔滨工业大学出版社,2007.
[4] 李团结,贾建援,胡雪梅.机械工程中两类非线性方程组的完全解[J].西安电子科技大学学报:自然科学版,2005,32(1):71-74.
[5] 郭仁生.机械工程设计分析和MATLAB应用[M].北京:机械工业出版社,2008.
[6] 高会生,李新叶,胡志奇.MATLAB原理与工程应用[M].2版.北京:电子工业出版社,2006.
[7] 周品,何正风.MAT LAB数值分析[M].北京:机械工业出版社,2009.
[8] 雷培,刘云霞.基于M ATLAB的四连杆机构运动分析[J].机械工程与自动化,2009(4):74-76.

