基于Butterfly细分规则的虚拟作物DFFD形态建模

林金花， 刘晓东， 刘国荣， 陈满林

(1.长春工业大学软件职业技术学院，吉林长春 130012; 2.西安交通大学电信学院，陕西西安 710049)

0 引 言

对虚拟作物进行动态外观改变及静态分析是虚拟作物研究的重要组成部分。目前变形方法有很多种，传统的非自由变形技术可以生成许多类型的三维几何形状，容易编辑，但是仅能用于特定的几何形体的变形，变形灵活性差，不能实现复杂物体的变形。在80年代提出的基于三维网格控制的自由变形技术(Free-Form Deformation，FFD)[2]采用不同的基函数定义映射关系，即均匀B样条基函数有理Bernstein基函数、NURBS基函数等，适用范围比较广泛，但是变形算法比较复杂，计算量大，不易操作。针对以上不足又出现了基于参数曲面的自由变形算法，这种方法空间开销小，变形速度快。但采用B样条张量积曲面控制的矩形网格是规则网格，难以贴合拓扑复杂的农作物植株外形，控制手段不够灵活。

近年来，细分曲面技术[3]和自由变形方法快速发展并得到了广泛的应用。DFFD方法将Voronoi图和Sibson局部坐标系引入变形过程中，具有更大的变形灵活性和通用性;细分曲面是通过用低分辨率的控制网格和定义在控制网格上的细分规则来表示光滑曲面的，规则简单，拓扑适应能力强。而虚拟作物的形态相对于其它规则物体比较复杂，使用传统的变形方法就需要初始控制网格足够细致，计算量成倍增加，采用细分技术可以实现用较少的控制点变化来控制物体的整体变形，使得变形具有控制网格为任意拓扑结构的FFD方法的灵活性，又保持了基于细分曲面控制的变形技术的低计算开销。文中基于Butterfly细分规则来对虚拟作物进行DFFD形态建模，针对传统DFFD方法的局限性，对其控制点集构造方法进行扩展，运用Butterfly细分方法对初始网格模型进行细分，选取出控制点集，并在细分后曲面上使用新的距离计算规则，用来模拟三维曲面的变形特征。因此，文中通过用Butterfly细分规则扩充DFFD方法更好地模拟了虚拟作物植株形态特征。

1 Butterfly细分规则及DFFD方法扩充

蝶形(Butterfly)细分算法是 1990年由Dyn[4]等人提出的一种基于三角网格的插值型细分曲面算法。算法在每一次细分过程中将三角形面片一分为四，只对每条边生成新的边顶点，保留上一次细分的网格顶点，使得一个三角片变成4个三角片。为获得更加逼真的建模，Zorin[5]等人对蝶形细分进行了改进，使得奇异点处具有更好的光滑性。

文中针对作物植株的特征，利用蝶式细分思想在DFFD方法基础上扩充了控制点集和Sibson坐标的构造方法，通过改变物体点坐标重新计算Sibson邻居中与该点关联的细分后控制点坐标实现变形。下面对文中采用的细分规则和扩充DFFD方法进行详细描述。

改进的Butterfly细分模板如图1所示。

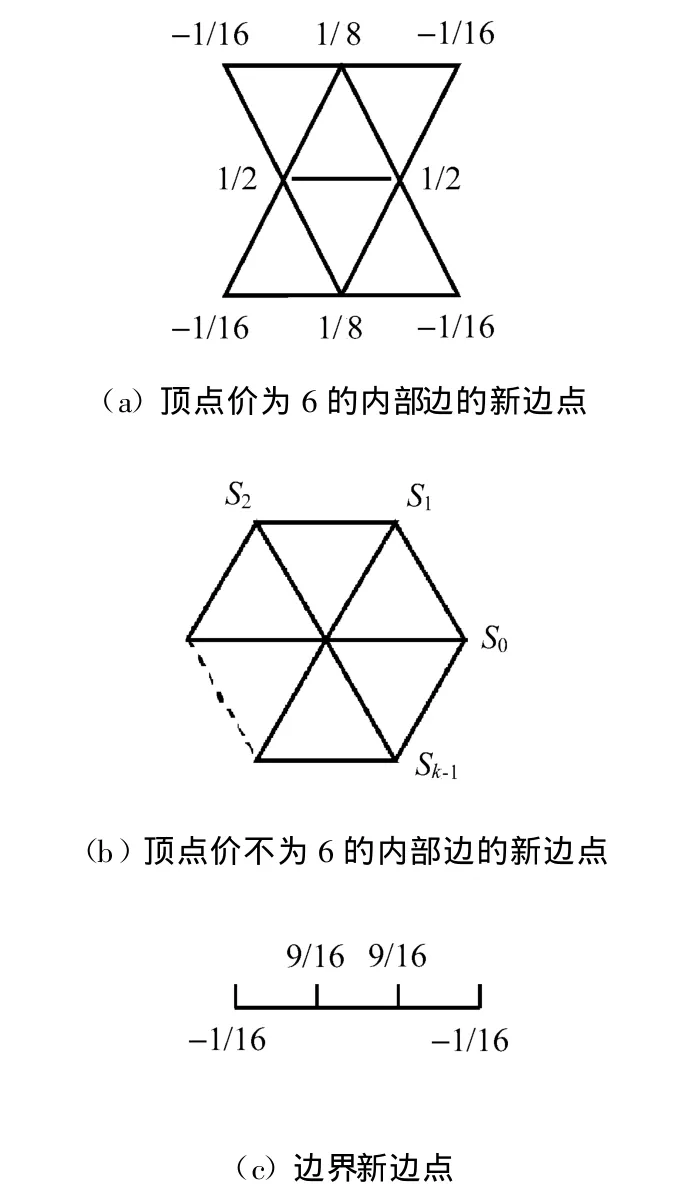
图1 改进的Butterfly细分模板

对Butterfly细分规则的描述如下:

1)连接的两个顶点的价均为6的边。对于该类边的8点格式来获得对应这类边的新顶点(见图1(a))。

2)连接的两个顶点，一个顶点的价为6，另一个顶点的价n≠6的边(见图1(b))。对于该类边，Q=0.75是对应顶点价为6的权值，而对应价n≠6的顶点的权值表示为:

式中:n——点的个数。

3)连接的两个顶点的价均不为6的边。对于这类边，分别以该边的两个顶点为参考点，在该边算得两个新顶点，然后取这两个新顶点的平均值作为对应该边的新顶点。

4)如果给定的三角形网格是带有边界的(见图1(c))，那么Butterfly细分算法在边界上产生的新点采用4点细分格式，计算新边点的公式为:

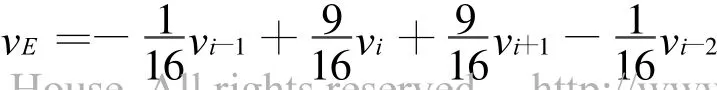
文中扩充的DFFD方法描述如下:

1)利用Butterfly插值细分方法的原点不变性，筛选出控制点与非控制点集。算法首先对初始网格上的每个顶点建立其邻接顶点的逆时针顺序表以及邻接顶点的权重系数列表;其次对三角面片应用Butterfly细分规则，将坐标不动点填加到控制点集，进行阈值设定和曲面求交确定与物体点相关联的控制点集(Sibson邻居);最后，重新计算每个面和顶点的法向矢量，生成新的网格模型。

2)重新计算Sibson坐标[6]。算法首先设 pi为要移动的物体点，计算pi所在的Voronoi[7]单元面积(即点集所组成三角面片的面积之和)，以及pi的Sibson邻居在细分前的Voronoi单元与pi在细分后的Voronoi单元的交集的面积;其次，改变物体点坐标，计算控制点偏移量Δp;最后得到pi的新位置坐标p′为:

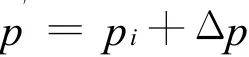
算法的工作流程如图2所示。

图2 算法框架

根据Sibson坐标，对细分后模型中与每个非控制点相邻的控制点进行偏移量的计算，最终生成的新坐标就是变形后物体点的坐标值。

2 虚拟作物的形态模拟

选取作物模型的局部器官组成初始模型，利用扩充的DFFD方法对初始模型进行变形，来模拟作物模型的局部特征，采用Java3D API进行绘制渲染。下面以小麦叶和水稻植株的形态模拟为例来说明基于Butterfly细分规则的虚拟作物的DFFD建模过程。首先建立原始小麦叶模型，选取得到初始控制点集，然后对小麦叶进行变形，模拟单个水稻植株穗，最后将单个植株组装成完整的水稻植株[8]。

2.1 小麦叶建模

小麦叶模型是由很多网格构成的多面体，我们将组成网格的三角面片的主线和边缘部分进行采样，组成初始控制点集，渲染后形成待变形物体的初始模型。首先初始化一组中心基线的控制点坐标，建立一组支撑线矢量[9-10];然后通过坐标旋转到新的坐标系即X′O′Y，得到变换矩阵，可以计算出由支撑线决定的边缘点的绝对坐标;最后计算得到边缘线上的所有点的坐标。经过渲染之后的小麦叶效果如图3所示。

图3 初始小麦叶模型

2.2 单植株变形

对初始小麦叶模型进行Butterfly细分，可以得到除控制点外的物体点坐标，将其作为变形操纵的非控制点集，再将叶片宽度偏移量设为0.01，叶片长度偏移量为-0.8，叶面弯曲点偏移量为0.1，叶面弯曲角偏移量为-20，叶鞘宽度和叶鞘长度设为0.01，根据偏移量计算生成物体点上新的Sibson坐标，经过渲染后生成的效果如图4所示。

图4 生成水稻单植株效果图

通过设置不同的偏移量来控制小麦叶变形，生成各种不同形态的水稻单植株叶片，效果如图5所示。

图5 小麦叶与4组水稻单株效果图

2.3 组装成水稻植株

通过设置不同的变形参数偏移量，应用文中算法，可用小麦叶来模拟各种形态的水稻单植株显示效果，一方面将这些单植株模型以Z轴方向设置绑定关系;另一方面通过设置多种参数使得单植株更具有真实感。绑定后的水稻植株效果如图6所示。

图6 小麦叶模拟的水稻植株

3 结 语

提出的一种基于Butterfly细分规则的虚拟作物DFFD建模方法能够对形态结构较为复杂的虚拟作物进行变形模拟，并且通过Butterfly细分规则选取变形控制点，实现了对DFFD方法的扩充，进而解决了三维虚拟作物的变形模拟问题。实验生成的用小麦叶模拟的水稻植株较为逼真，能够满足虚拟环境的需要。

[1] Moccozet，Thalmann N M.Dirich let free-form deformation and their app lication go hand simu lation [J].Proceeding of the Com puter Animation，1997: 93-102.

[2] Sederberd T W，Parry S R.Free-form deformation of geometric models[J].ACM SIGGRAPH，1986，20:151-160.

[3] Su Z X，Li B J，Liu X P，etal.Rapid evaluation o f regular quad-mesh interpolatory subdivision surfaces based on parametric decomposition[J].Journa l o f Softw are，2007，18:18-25.

[4] LiB J，Liu X P，Yu BW，et al.Exactevaluation of interpo latory subdivision surfaces at rational parameters[J].CKJC，2008，18:175-179.

[5] H u SM，Zhang H，Tai C L，etal.Directmanipulation of FFD:Efficient explicit solutions and decomposiblemultip le point constraints[J].The Visual Computers，2010，17(6):370-379.

[6] 李桂清.细分曲面造型及应用[D]:[硕士学位论文].北京:中国科学院计算技术研究所，2007.

[7] 张景峤.细分曲面生成及其在曲面造型中的应用研究[D]:[硕士学位论文].杭州:浙江大学，2007.

[8] 郭际香，黄晓蓉，章毅.三维空间中的Dirichlet自由变形算法[J].电子科技大学学报，2007，36(3):24-27.

[9] 王金生，韩臻，施寅.几种经典网格细分算法的比较[J].计算机应用研究，2009，21(6):45-48.

[10] 陈玉国，李宝军，苏志勋，等.Butterfly细分曲面的快速求值[J].工程图学学报，2009，33(3):124-128.