基于WVD的调频引信瞬时频率估计算法

袁汉钦，张向龙

（1.海军驻景德镇地区航空军事代表室，江西 景德镇 333001；2.海军驻绵阳地区军事代表室，四川 绵阳 621900）

0 引言

调频引信系统中的差频信号在时间和频率两个方向都包含有目标的距离信息。因此，调频引信系统设计中的一项重要的工作就是研究差频信号的瞬时频率估计算法[1]。传统的调频引信对差频信号的频率估计是以时不变系统为基本模型的，估计结果存在固定误差，无法实现连续测距[2-3]；而利用时频分析的方法，可得到信号在时间和频率上的二维能量分布信息。因此，将时频分析应用于引信差频信号的瞬时频率估计，可得到差频信号随时间的连续分布，进而能够更加精确地检测出弹目距离。

1 WVD最大值提取信号瞬时频率的算法

时频分布种类很多，其中，Wigner-Ville分布(WVD)就是一种最常用的时频分布。

信号f的Wigner-Ville分布 Wf(u,ξ)定义为[4]：

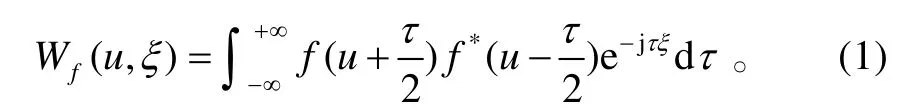
它能精确地定位信号f的时频结构。如果f的能量在时域上集中在u0，在频率上集中在ξ0，则Wf的能量集中在(u0,ξ0)，其时频宽度与f的相同。记fa是f的解析函数，可写成 fa(t)=a (t)exp[jϕ (t)]，则瞬时频率

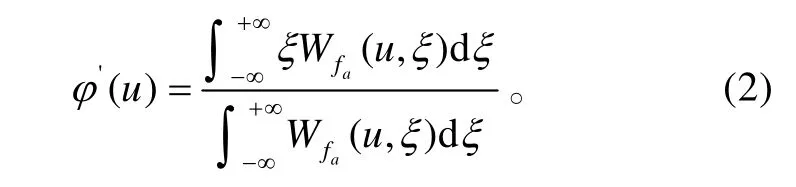
式(2)说明，对任意固定的u，Wfa(u,ξ)的能量主要集中在瞬时频率 ξ=ϕ'(u)的邻域内。因此，可以直接使用Wfa(u,ξ)的谱峰检测来估计瞬时频率，即WVD分布中每个时刻最大值对应的频率点就是信号在此时刻的瞬时频率。所以此算法的基本思想为提取WVD 每个时间点最大函数值对应的频率点为该时间点的瞬时频率估计值，这在高信噪比条件下有很好的估计性能，而且运算量较小[5-6]。

然而在低信噪比条件下，噪声的影响会使得最大值所对应的频率点偏离信号瞬时频率的真实值，引起较大的估计误差，具体的算法流程如图1所示：

图1 WVD最大值法流程图

使用最大频偏为30 Hz，周期为4 s的三角波调制频率为100 Hz，振幅为3 V的载波，并假设回波信号比发射信号延迟0.1 s，将回波信号和本振信号进行混频滤波，得到差频信号。在信噪比为−3 dB的条件下进行了仿真试验，对信号用WVD最大值法进行了处理，在采样频率为10 Hz时，得到的结果如图2和图3所示。

图3中虚线代表瞬时频率估计值，实线代表瞬时频率真实值。由图可看出由于信噪比降低，边缘效应和噪声的影响都很大，瞬时频率估计值与真实值之间的误差很大，所以在低信噪比条件下，此方法已经无法完成信号的瞬时频率估计。

图2 WVD结果

图3 IF估计结果

由图可看出，由于信噪比较低时，边缘效应和噪声的影响都很大，瞬时频率估计值与真实值之间的误差很大。所以在低信噪比条件下，此方法无法完成信号的瞬时频率估计。

2 SPWVD最大值提取差频信号瞬时频率的算法

尽管Wigner-Ville分布具有时频能量聚集性高等好的性质，然而从上节分析中可以看出交叉项干扰的值甚至可能比有用信号分量的值大，严重影响了对有用信号的分析和提取。采用SPWVD可有效降低交叉项的影响，该方法在时域和频域同时对WVD结构做平滑[7-8]，其定义为

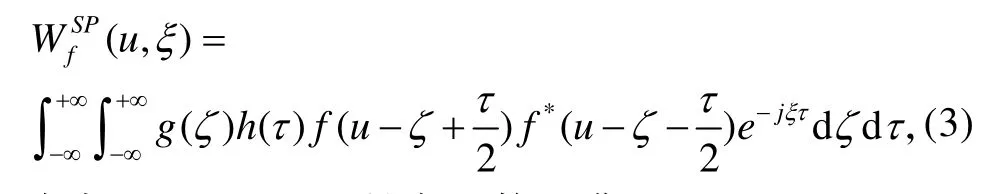
式中：h (t)和g (t)是窗函数，满足 h(0)=G (0)=1；G (f)表示 g (t)的傅氏变换。

得到SPWVD后，再提取SPWVD每个时间点最大值对应的频率值作为信号的瞬时频率估计值，具体算法流程如图4所示。

图4 SPWVD最大值法流程图

采用和上节一样的仿真条件，虚线代表瞬时频率估计值，实线代表真实值，如图5～6所示。

图5 SPWVD结果

图6 IF估计结果

由图6可以看出SPWVD有效的抑制了噪声，从而降低了交叉项干扰，由于此算法提取的是最大值，所以时聚性的降低对估计效果影响不大，通过比较可以得出：在相同信噪比条件下，SPWVD最大值法的估计性能明显优于WVD最大值法。

3 SPWVD与Viterbi相结合提取差频信号瞬时频率的算法

3.1 Viterbi算法

此算法的基本思想来源于数字图像处理，原理与连接地图上两点使得其长度和高度变化都尽可能小的原理相似。[9-10]

考虑时间间隔 n ∈[n1,n2]，n1、n2之间的所有路径属于K，瞬时频率估计即为使得下面表达式最小的路径

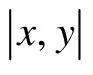
式中：p (k (n);n1,n2)是由 n1到n2沿路径 k (n)的代价函数g (x,y)与f (x) 之和。函数关于是非减的(两个连续点x=k (n)，y=k (n−1)的瞬时频率值)，f (x)是关于 x=SPWVD (n,k (n))的非增函数。这样，就能保证在某时刻SPWVD的较大值更有可能成为信号的瞬时频率值。

在某时刻n，函数f (x)通过下面的过程形成：把所有时刻点的SPWVD值SPWVD (n,ω)按从大到小的顺序排列

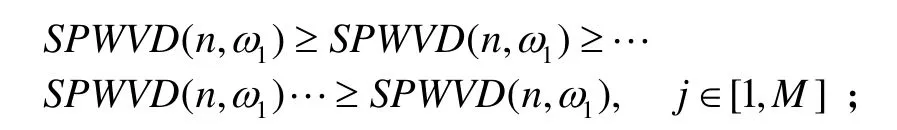
M为信号频率点数，则f (x)的形式定义为

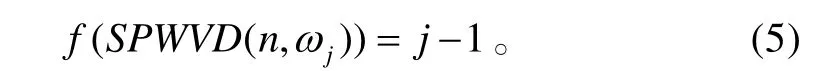
这样可以保证SPWVD的较大值作为瞬时频率估计值，使用这种形式的原因是SPWVD在强噪声环境下，瞬时频率值是第j个最大值的概率随j 线性降低。由于信号和噪声的参数是时变的，f (x)与SPWVD的值无关。

若 g (x,y)=const，方程(3)的瞬时频率估计为SPWVD的最大值，即函数f (x)完全确定式(3)的最小值，本文采用线性形式的g (x,y)：

式(6)中：Δ的最优选择为两个连续点瞬时频率变化的最大期望值，即对于较小的瞬时频率变化代价函数为0，在试验中选取较小的Δ(如Δ=3)可以得到很好的效果，当Δ →∞时为估计WVD的最大值。注意，上面提到的式(4)和式(5)只是代价函数f (x)和g (x,y)的一种形式。

3.2 SPWVD与Viterbi相结合的算法

利用平滑可以有效抑制噪声的优点，将SPWVD与Viterbi算法结合进行差频信号的瞬时频率估计。首先，在WVD后进行平滑，得到SPWVD处理结果；然后，进行门限处理；最后，通过Viterbi方法得到差频信号的瞬时频率估计结果，具体算法流程如图7所示。

图7 Viterbi-SPWVD算法流程图

仿真结果如图8所示，信噪比为−3 dB，虚线为估计差频信号瞬时频率，实线为真实频率。可以看出采用该算法估计差频信号与实际信号误差很小，能很好地抑制噪声和交叉项的干扰。

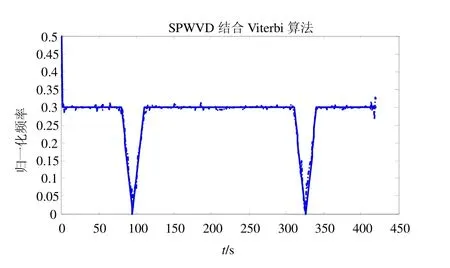
图8 IF估计结果(SNR=−3dB)

4 结束语

将调频引信差频信号在不同的信噪比情况下分别进行400次Monte Carlor仿真，得到瞬时频率的估计值方差随信噪比变化的关系图如图9所示(虚线为基于WVD最大值法的估计方差，点线为基于SPWVD最大值法的估计方差，点实线表示基于Viterbi-SPWVD 算法的估 计 方 差)。基 于Viterbi-SPWVD算法提取瞬时频率在信噪比不低于−1 dB时可以较精确的估计差频信号频率，WVD最大值法、SPWVD最大值法分别在2 dB和4 dB条件下可以估计差频信号频率。可见，利用时频分析的方法可有效检测出引信差频信号的瞬时频率，进而得到距离的连续估计，其中Viterbi-SPWVD算法在低信噪比情况下的性能更为优越。

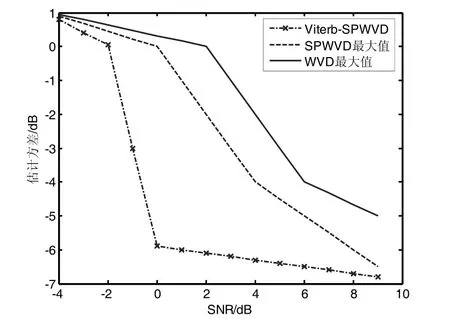
图9 瞬时频率估计方差

[1]路翠华,李国林,熊波.基于变步长LMS算法的线性调频引信噪声抑制[J].海军航空工程学院学报,2010,25(5):549-551.

[2]崔占忠.调频测距信号分析[J].探测与控制学报,2006,28(5):1-3.

[3]周祖国,李元光,刘芒龙,等.基于瞬时相位的三角波调频差频信号数学模型[J].探测与控制学报,2009,31(3):77-80.

[4]BOASHASH B,WHITE L,IMBERGER J.Wigner-ville analysis of non-stationary random signals[C]//ICASSP.Tokyo,Japan:IEEE,1986:2323-2326.

[5]胡旭娟.时变信号检测与瞬时频率估计方法研究[D].西安:西北工业大学,2007.

[6]STANKOVIC L J,STANKOVIC S.An analysis of instantaneous frequency representation using time-frequency distribution-generalized Wigner distribution[J].IEEE Transaction on signal processing,1995,42(2):245-266.

[7]SI WENRONG,LI JUNHAO,YUAN PENG.Study on time-frequency characteristic of PD pulse using Wigner-Ville Distributions[C]//ISEI.Vancouver,Canada:IEEE,2008:355-358.

[8]AMIRMAZLAGHANI M,AMINDAVAR H.Modeling and denoising Wigner-ville distribution[C]//DSP/SPE Marco Island,FL:IEEE,2009:530-534.

[9]LOU H.Implementing the Viterbi algorithm[J].Signal Processing Magnine,1995,12(5):42-52.

[10]栾海妍.基于时频分析的跳频信号检测与特征提取[D].郑州:解放军信息工程大学,2007.