防空武器系统火力兼容模型研究

由大德，张发强，余鹏飞

（1.西北工业大学航海学院，西安 710072；2.海军大连舰艇学院导弹与舰炮系，辽宁 大连 116018）

单武器系统防空作战模式已经远远不能适应水面舰艇的现代作战环境，要求必须充分使用全舰的防空火力，综合协同使用所有防空武器以达到对空袭目标(尤其导弹目标)进行最密集和最有效的火力抗击。但是由于不同防空武器的特性不同，需要多种防空武器合理协同使用，以避免武器间的火力冲突现象，从而提高整体防空效果。研究避免防空武器系统火力冲突现象发生的问题属于为火力兼容问题[1]，通常可以从空域和时域两个方面进行分析[2]。

本文以防空导弹与火炮武器协同使用情况为例，从防空武器弹道交叉情况入手，在分析防空武器系统的火力兼容要求的基础上，建立防空武器系统的火力兼容模型。

1 防空武器系统协同使用时的火力兼容要求

对空防御作战中，防空导弹与火炮弹丸相互冲突、弹道交叉的判断条件并不是射弹在空中完全相遇或发生撞击，而是两种射弹在不同的弹道位置都要求存在某一特定的距离。当外界干扰进入这个距离范围以内时，就可能对射弹的正常飞行和最终的抗击效果产生影响。因此，不同防空武器实际弹道之间的空间距离在同一时刻必须不小于要求的特定距离值，否则就认为它们的火力是不兼容的，可将这个特定距离称为火力兼容的弹道最小安全距离。

为了使防空导弹和火炮弹丸之间互相不造成影响，要求在射弹飞行过程中的任意时刻，防空导弹和火炮弹丸两者之间的距离 ΔD 要始终不小于安全距离 Lmin。这可近似看作是以不同运动规律运动的两个质点之间的最短距离问题[3-5]。

建立任意空间直角坐标系OXYZ，如图1所示，(xd(t1),yd(t1),zd(t1))表示 t1时刻的防空导弹位置坐标；(xP(t2),yP(t2),zP(t2))表示 t2时刻的火炮弹丸位置坐标。

图1 防空武器火力兼容判断示意图

则上述问题可以表达为：

实际情况中，防空武器弹道的计算是复杂繁琐的。但由于防空导弹与其他防空武器协同使用时的火力冲突通常发生于直飞段，所以可以近似以防空武器的理论弹道为研究对象[3]，而且研究的重点也在于防空导弹直飞段与火炮武器的火力兼容问题。如果以防空导弹的发射时刻为零时刻，防空导弹的直线段飞行时间为T，防空导弹和火炮的发射时刻间隔为ΔT，则在t时刻的ΔD值可以表示为：

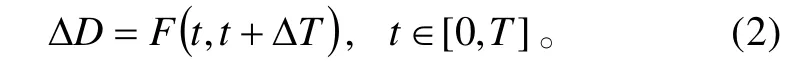
防空导弹与火炮弹道确定后，ΔT就决定了防空导弹和火炮弹丸沿各自弹道飞行过程中的距离ΔD。则火力兼容的距离要求条件就转化为对发射时刻间隔ΔT的要求，即：

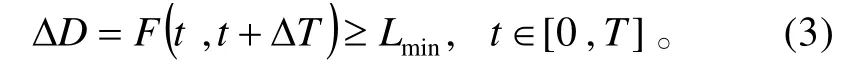
2 防空导弹与火炮武器火力兼容模型的建立

建立图2所示空间直角坐标系。

图2 防空导弹与火炮武器火力兼容示意图

图2中：坐标系OXYZ以防空导弹发射架为原点，平面OXY为水平面，以舰首方向为X轴，以左正横方向为Y轴，以垂直水平面向上方向为Z轴；坐标系O' X'Z'以火炮发射架为原点，以火炮弹道在水平面内的投影为X′轴，以垂直水平面向上方向为Z '轴，坐标系O' X'Z'中 X '轴的方向是随火炮的射击舷角变化而变化。Cd为防空导弹的射向；Cp为火炮武器射向；c为弹道交叉点；L为防空导弹发射架和火炮发射架间的距离；α为防空导弹的射击舷角；θ为防空导弹的射击俯仰角；β为火炮的射击舷角；σ为火炮武器的射角；ΔD为防空导弹弹道上任一点d与火炮弹道上任一点p 两点间的空间距离；Dd为d点对应的防空导弹飞行距离；Dp为p点对应的火炮弹丸飞行距离。

在防空导弹飞行时间T时刻，以 (xd,yd,zd)、(xp,yp,zp)分别表示防空导弹和火炮弹丸于坐标系OXYZ 内的位置坐标，(x′p,y'p)表示火炮弹丸于坐标系O' X'Z'内的位置坐标，则ΔD可以表示为

式中：

V (t)为防空导弹的实时飞行速度。

可以通过龙格库塔法解标准条件下的火炮弹道微分方程组求得p点的坐标 (x′p,y'p)[6]，此时的火力兼容模型就可表示为：

对于防空导弹：射击诸元中射击舷角α和射击俯仰角θ 确定后，防空导弹现在点坐标 (xd,yd,zd)取决于防空导弹的速度时间方程表达式 V (t)和防空导弹飞行时间T。

对于火炮武器：弹丸初速 Vo、射角 θo和弹道系数C 确定后，(x′p,y'p)取决于弹丸飞行时间[6-7]。火炮射击舷角β 确定后，则火炮弹丸的现在点坐标(xp,yp,zp)同样只是弹丸飞行时间的函数。

从上面的分析可知：防空导弹和火炮弹丸的飞行时间都是由发射时刻和速度特性确定的。当速度特性确定之后，防空导弹和火炮武器交叉射击时是否火力兼容最终由各自的发射时刻决定。所以，协调各防空武器的发射时间、确定各武器的间隔开火时间，就成为解决防空武器火力兼容问题的关键。

3 火力兼容模型简化及分析

1)火力兼容模型简化。

将图2坐标系简化为水平坐标系，坐标系OXY以防空导弹发射架为原点，以舰首方向为X轴，以水面正横方向为Y轴，如图3所示。

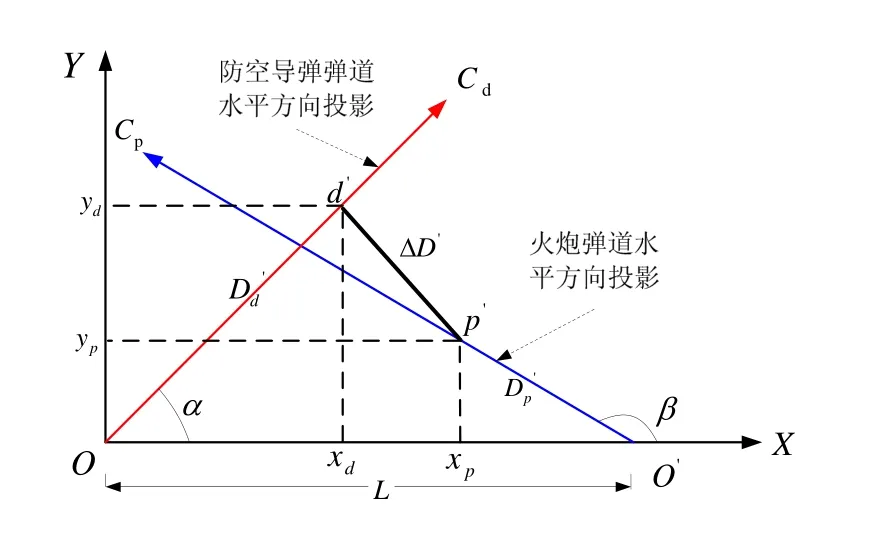
图3 防空导弹与火炮交叉射击水平示意图

图3中：Δ D'为防空导弹弹道水平投影上 d '与火炮弹道水平投影上 p '两点之间的距离；Dd'为防空导弹发射T时间后飞离发射架的水平飞行距离；为火炮开火t时间后炮弹飞离炮口的水平飞行距离。则：

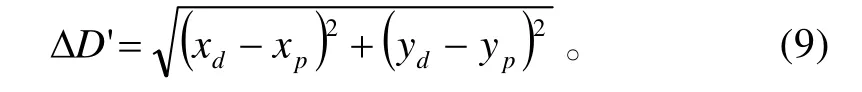
在此坐标系内，假设防空导弹和炮弹弹丸水平之间的距离ΔD' 始终满足

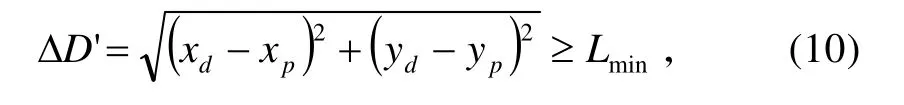
式中：

由于 ΔD ≥ΔD'始终成立，所以满足式(10)的情况必满足式(8)。因此，防空导弹与火炮武器的火力冲突问题便转化为水平射程上的相互追击问题。整理式(10)可得简化的火力兼容模型：

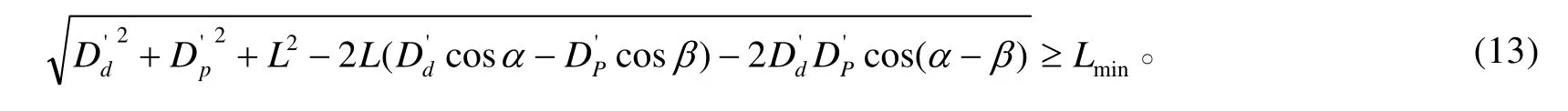
2)火力兼容基本条件求取。

防空导弹和火炮交叉射击时，如果导弹先射击，那么至少要等到导弹飞离发射架后导弹弹体与火炮发射架的距离大于安全距离 Lmin后，火炮才可以开火射击。那么当防空导弹距火炮发射架距离为Lmin时，火炮还未开火，即 D 'p为0，则：

整理可得：

式中，L、Lmin和α均为已知量。

所以式(15)是以 Dd'为未知数的一元二次方程。

假设火炮的推迟开火时间为Δt，此时T=Δt。

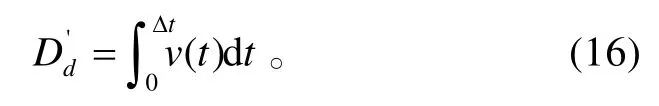
由此可见，只要知道防空导弹速度与时间方程，式(16)就是以积分上限 Δt为未知数的方程，求解方程可以得到在交叉射击情况下，防空导弹以任意的α角(防空导弹的射击方向与舰艏向的夹角)射击时，火炮的推迟开火时间 Δt。同理，可按下式求取火炮以β角(火炮的射击方向与舰艏向的夹角)先于防空导弹射击时防空导弹的推迟开火时间 Δt。

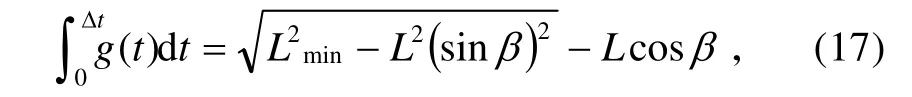
Δt 只是满足防空导弹与火炮武器火力兼容的基本条件，并不能保证两种射弹后续飞行过程中的间隔距离始终大于安全距离 Lmin。因此，既要求两种武器的发射间隔不能小于 Δ t，还需要进一步对防空武器火力兼容条件进行分析。

3)火力兼容条件求取。

对式(13)进一步整理可得到：

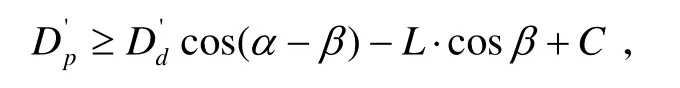
或

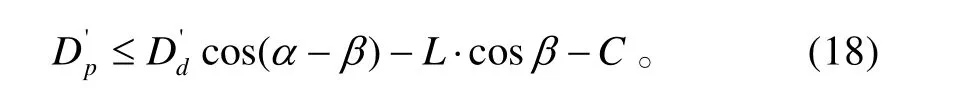
式(18)中：

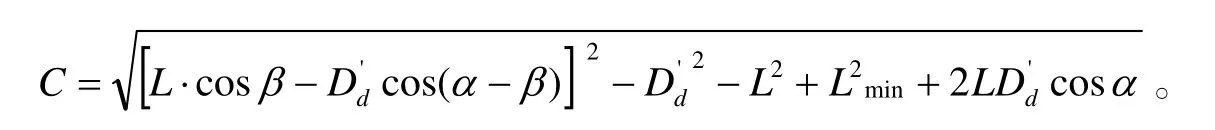
可以看出：在L、Lmin、α和β都已知的情况下，Dd'决定的取值。通过前面分析已知，如果取先发射的防空导弹的发射时刻为零时刻，T代表防空导弹的飞行时间，火炮间隔ΔT时间后开火，则有：

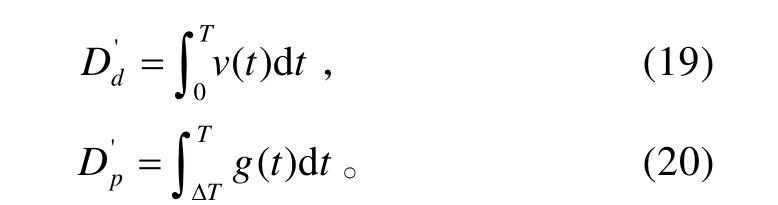
为满足防空武器火力兼容的要求，ΔT的取值应该使得在整个防空导弹飞行时间段[0，T]内的任意时间 T′(T ′∈ [0,T])，以T′为积分上限的Dd'和D'p都满足式(18)。当然，如果火炮先于防空导弹某一时间开火，而且仍然取防空导弹的发射时刻为零时刻，那么要使式(18)成立，火炮的开火时间将比防空导弹开火时间提前 ΔT[8]。

以假设型防空导弹和火炮为例，防空导弹先于火炮发射，以不同的延迟时间间隔和不同射角对水平射程进行仿真计算，图4和图5分别给出了间隔1.5 s和3 s的水平射程曲线仿真结果图。

图4 火炮延迟1.5 s发射的水平射程曲线

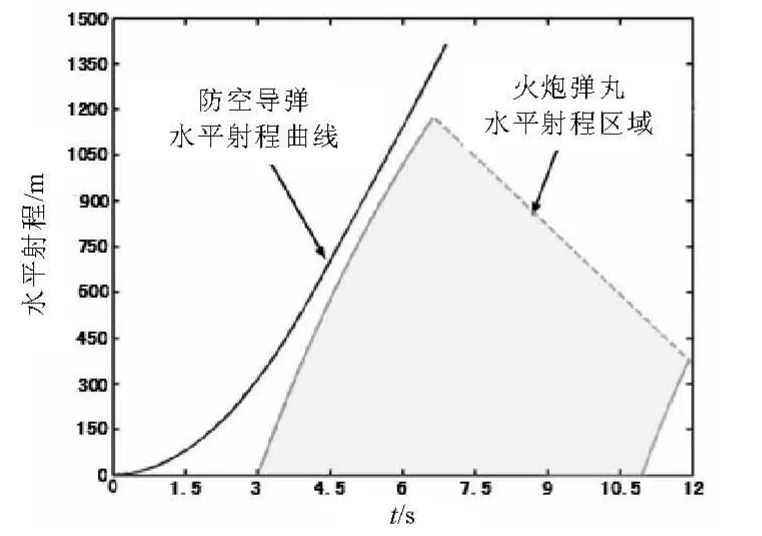
图5 火炮延迟3 s发射的水平射程曲线

可见，防空导弹发射后间隔1.5 s 火炮再发射，两种武器在水平射程上仍然存在严重的冲突，不满足火力兼容的条件；防空导弹发射后间隔3 s 火炮再发射，两种武器在水平射程不存在冲突，满足火力兼容的条件。因此，可以认为在防空导弹与火炮协同使用的过程中，满足火力兼容的条件是：如果防空导弹先发射，那么至少延迟3 s 火炮才能发射。

4 结束语

本文针对防空导弹与火炮武器使用时弹道交叉引起的火力冲突问题进行了研究，提出了防空导弹与火炮武器协同抗击时的火力兼容要求，建立了防空武器系统的火力兼容模型，并结合实际对所建模型进行简化和求解分析，所建模型客观实际、便于计算，为深入研究防空武器协同使用时的火力兼容冲突问题提供理论依据，从而提高防空导弹与火炮武器协同作战能力，具有理论和实用价值。

[1]由大德,王峰.水面舰艇防空火力兼容问题[J].火力与指挥控制,2004,29(4):49-50.

[2]于崇飞,由大德.弹炮协同火力兼容安全时间分析[J].海军大连舰艇学院学报,2008,31(5):30-32.

[3]李涛,由大德.水面舰艇防空火力兼容系统作战仿真模型[J].海军大连舰艇学院学报,2005,28(5):4-7.

[4]鲜勇.弹道并行计算的设计与实现[J].飞行力学,2003,21(1):59-61.

[5]李亦伟.水面舰艇火力兼容技术研究[J].舰船电子工程,2009,29(1):21-22.

[6]汪德虎,谭周寿,王建明.舰炮射击基础理论[M].北京:海潮出版社,1998:108-123.

[7]王建明,汪德虎.舰炮对空射击[M].大连:海军大连舰艇学院,1999:30-32.

[8]由大德,于崇飞.防空武器优先使用问题研究[J].海军大连舰艇学院学报,2008,31(4):10-12.