基于遗传算法的MIMO雷达正交编码信号波形优化

李晓明，罗钉

(1.中航雷达与电子设备研究院航空电子系统射频综合仿真实验室，江苏无锡214063;2.北京航空航天大学电子信息工程学院，北京100083)

MIMO雷达通过在不同天线上发射接收正交信号，利用目标的空间分集机制改善目标的检测性能［1，6－7］。为最大程度地发挥MIMO雷达的优势，系统对发射信号的设计提出了更高的要求:首先，与传统的单基雷达一样，要求发射信号为大时宽、宽带宽的脉冲信号，在接收端对大时宽、高带宽的信号进行压缩处理，从而得到脉冲宽度为信号带宽倒数的窄脉冲信号，解决雷达探测距离和分辨率之间的矛盾。压缩输出信号须具有高的主副瓣比，以避免弱目标被强目标副瓣淹没和副瓣带来的错误检测;其次，由于MIMO内各信号间的干扰也不容忽视，所以它还要求网络雷达系统内各发射机发射的信号互不相关，从而使雷达在不同方位获得独立的空间分集增益［6－7］，并降低雷达间干扰带来的虚警概率。

相位编码压缩和时间频率编码压缩技术是常用的脉冲压缩技术，要找到一组L个码长为N的具有高分辨特性的正交多相或多频编码信号是一个典型的非线性优化问题。基于概率模型的遗传算法［8－9］是解决非线性寻优的一种有效方法，具有智能化全局寻优，且收敛性不受初始值限制的优点。文中将MIMO雷达发射信号的自相关函数副瓣峰值和互相关函数的峰值之和作为目标函数，通过构造适应度函数，利用遗传算法实现发射信号波形优化设计。仿真结果和实验分析验证了该算法的有效性和可行性。

1 正交MIMO雷达发射编码信号模型

考虑正交MIMO雷达有L个发射天线，每个天线均发射相互正交的编码脉冲信号{sl(t)，l=1，2，3，…，L}，每个信号有N个持续时间为T1的子脉冲组成。由于信号间的正交性，那么任意两个发射信号自相关函数满足

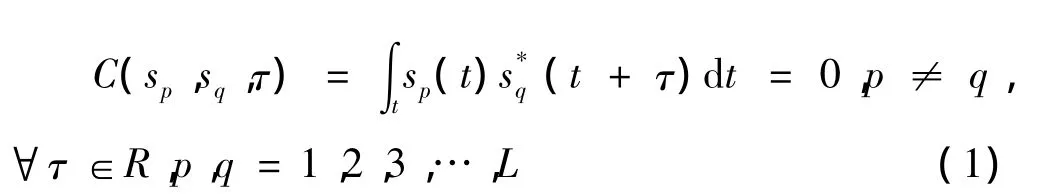
其中，“*”表示共轭运算操作符号。为使信号具有高的距离分辨力，信号的非周期自相关函数有以下形式

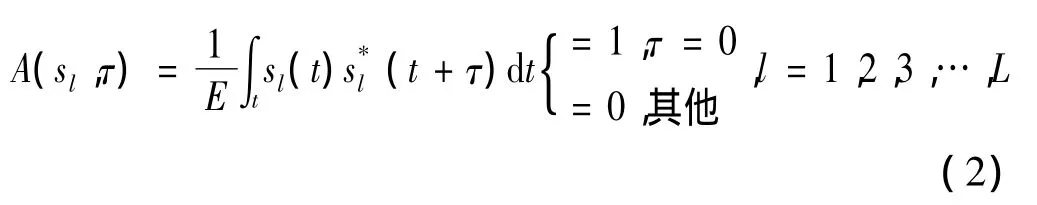
其中E为信号sl(t)能量。

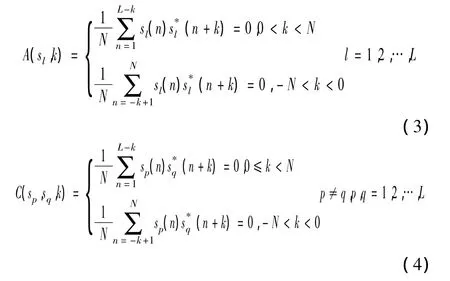
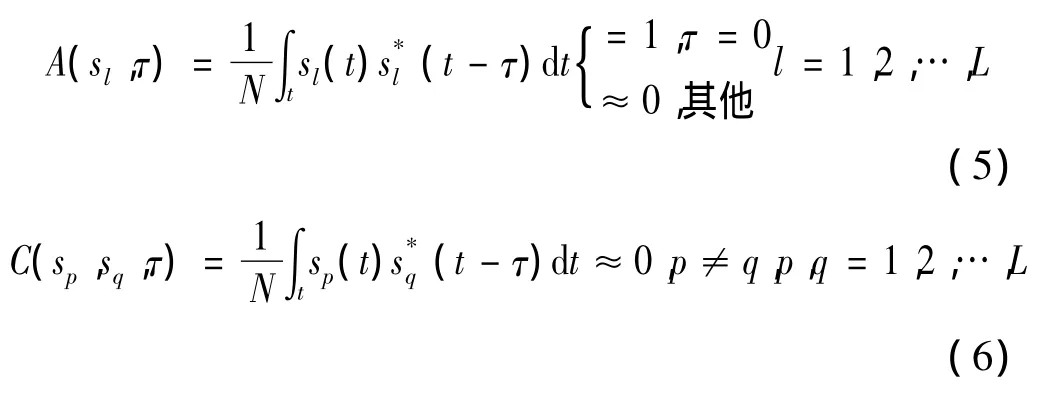
2 信号波形优化设计算法

2.1 适应度函数构造

正交信号的性能可以由自相关函数的副瓣电平峰值(ASP)和互相关函数的电平峰值(CP)表征，受ASP和CP约束的代价函数

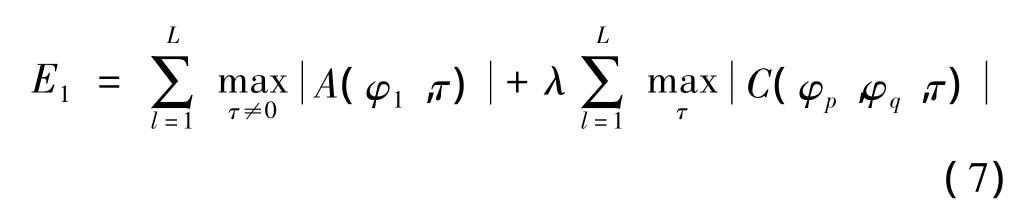
其中，λ为自相关函数与互相关函数之间加权系数。与遗传算法相结合，将代价函数转化为适应度函数

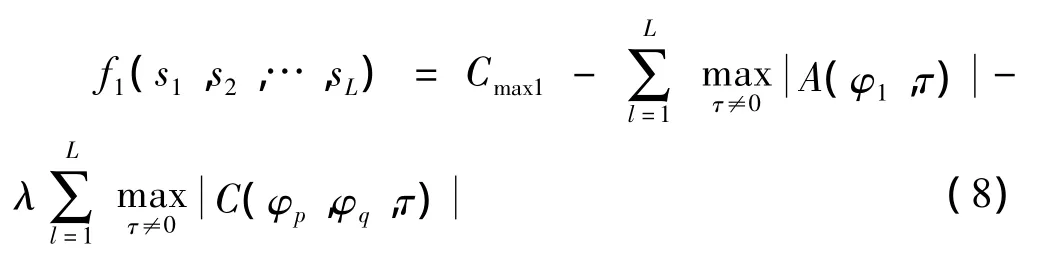
式中，λ此时为适应度因子，λ越大，表示互相关对环境的适应影响越大;Cmax1为E1的最大值，保证适应度函数的非负性。考虑互相关能量和自相关函数副瓣能量的分布，适应度函数

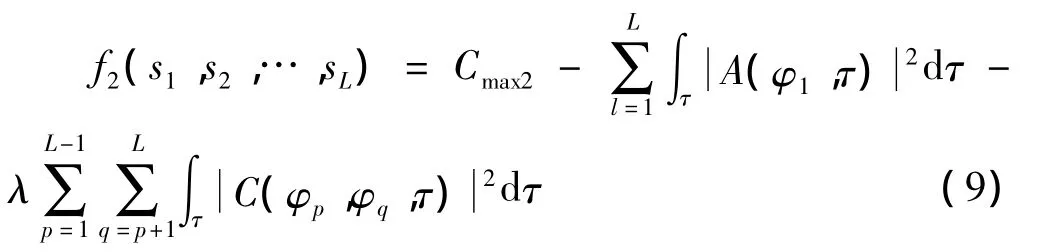
其中，Cmax2为自相关副瓣能量和互相关能量之和的最大值。适应度函数式(9)通过约束相关函数能量，均匀地分布在所有可能时刻上来最小化ASP和CP，具有良好的稳健性［10］。因此，在进行波形优化设计时，采用式(9)作为适应度函数。

2.2 基于遗传算法的正交多相编码序列优化设计

由于遗传算法主要模拟生物的进化过程进行搜索，而生物的进化过程主要通过染色体之间的交叉和变异来完成，所以需要对正交编码序列组模拟染色体进行二进制编码。鉴于多相编码序列本身就是一种多元伪随机序列，故采用二进制编码时，可以将每个相位状态向二进制数进行简单的映射。以常用的四相编码信号为例，则有，映射为二进制［00011011］，可以实现一对一映射。当相位状态M不能被2整除时，会出现2δ－M个冗余二进制编码，在交叉和变异操作中会出现二进制编码串，不能有效地编解码。为克服这一问题，当在交叉、变异操作后出现冗余编码时，在2δ－M各有效二进制编码串中随机选取一个来替代冗余二进制编码。用(0)表示初始化种群，(i)表示第i代种群。用遗传算法进行波形优化的过程如下:

Step2根据各个个体的适应度值，采用轮盘赌方式从第i代种群(i)中选择出一些优良个体遗传到下一代群体(i+1)中，并产生新的个体取代未选出的个体。

2.3 正交多频编码序列优化设计

由于多频编序列本身也是一种伪随机编码序列，在进行遗传编码时，将编码序列为的任意排列影射为一个多相编码序列。同时由于多频编码序列中每个码元的不可重复性，使得交叉操作不易进行，将采取扩大种群、加大变异概率等措施避免算法早熟。其主要步骤如下:

Step2根据各个个体的适应度值，采用轮盘赌方式从第i代种群(i)中选择出一些优良个体遗传到下一代群体(i+1)中，并随机产生新的个体更新未选出的个体。

Step3行变异操作，产生多个互异的随机变异位，然后将不同位置的码元随机互换，从而生成新的个体。为防止早熟现象，变异概率要比多相编码设计时的大，并采用自适应算法［10］进行对其进行自适应调节。

3 MIMO雷达波形优化设计结果分析

在进行正交多相编码信号设计时，主要参数为:种群大小P=100;起始交叉概率pc1=0.8;最小交叉概率pc2=0.5;起始变异概率pm1=0.05;最大变异概率为pm2=0.15;最大迭代步数为1 200。在进行正交多频编码信号设计时，主要参数为:种群大小P=150，起始变异概率pm1=0.10，最大变异概率为pm2=0.30最大迭代步数为2 000。

表1给出了L=4，N=40，M=4，λ=1时优化得到的一组正交多相编码序列的相位值，其中φl(n)∈多相编码信号的ASP和CP见表2。表2中对角线元素表示归一化ASP，其余元素表示不同信号间的归一化CP。ASP平均约为0.14或－17.2 dB，CP平均约为0.23或－13 dB。当式(9)中的λ由1变为1.5时，ASP和CP都约为0.17。实验表明，适应度因子对基于遗传算法的正交多相编码序列优化起到了有效的调节作用，增大λ意味着CP对适应度函数影响变大，使得CP降低，ASP升高。

表1 L=4，N=40，M=4设计出的正交多相编码信号相位序列

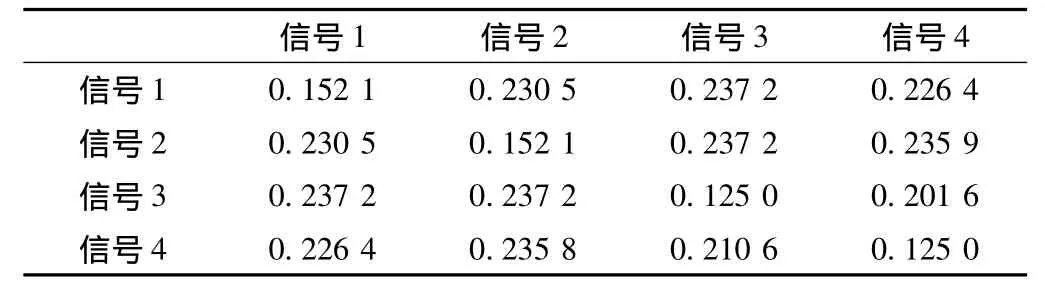
表2 L=4，N=40，M=4设计出的正交多相编码信号的ASP与CP

表3列出了L=3，N=32，λ=0.56时，优化得到的正交多频序列编码。表4给出了多频编码序列的归一化ASP和CP，其中对角线元素表示归一化ASP，其余元素表示不同信号间的归一化CP。ASP平均约为0.038 4或－28.3 dB，CP平均约为0.071或－23 dB。在其他条件相同的情况下，当式(9)中λ由0.56变为1.25时，ASP平均约为0.039 3或－28.1 dB，CP平均约为0.067 3或－23.4 dB。实验表明，适应度因子对基于遗传算法的正交多频编码信号优化起到了有效的调节作用，增大意味着CP对适应度函数影响变大，使得CP降低，ASP升高。

表3 L=4，N=32设计出的正交多频编码信号相位序列

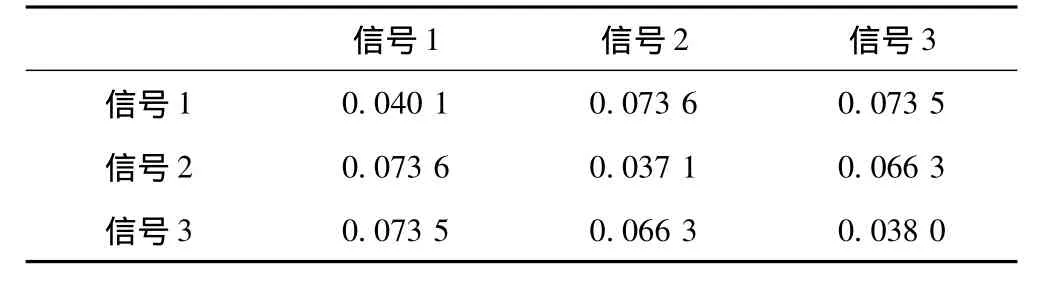
表4 L=4，N=32设计出的正交多频编码信号的ASP与CP

4 结束语

针对正交MIMO雷达对发射信号高分辨特性和正交特性的要求，提出了一种基于遗传算法为正交MIMO雷达优化设计正交编码信号的方法。它利用遗传算法具有整体非线性寻优的特性，通过非线性迭代搜索符合自相关和互相关特性要求的正交编码序列。计算机仿真和实验分析表明，采用本算法能够有效地设计出符合要求的正交多相和多频编码信号。

［1］ FISHLER E，HAIMOVICH A，BLUM R，et al．MIMO radar:an idea whose time has come［C］．IEEE International Radar Conference，Philadelphia，2004:71－78．

［2］ FISHLER E．Spatial diversity in radars－models and detection performance［C］．USA:IEEE Confress on Signal Pro，2004，4:26－33．

［3］ FISHLER E，HAIMOVICH A，BLUM R，et al．Performance of MIMO radar systems:advantages of angular diversity［C］．IEEE Trance on SignalPro，2004，56(10):303－312．

［4］ CHIZHIK D，FOSCHINI G J，GANS M J，et al．Valenzuela，keyholes，correlations，and capacities of multielement transmit and receive antennas［J］．IEEE Trans on Wireless Communications，2002，1(2):361－386．

［5］ FOSCHINIG G J，GANS M J．On limits of wireless communications in a fading environment when using multiple antennas［J］．WirelessPersonalCommunications，1998，6(3):311－318．

［6］ ROBEY F C，COUTTS S，WEIKLE D，et al．MIMO radar theory and experimental results［C］．IEEE Trance on Signal Pro，2004，56(3):555－563．

［7］ FISHLER E，HAIMOVICH A，BLUM R，et al．Spatial diversity in radars－models and detection performance［J］．IEEETransonSignalProcessing，2006，54(3):823－838．

［8］ 张文修，梁怡．遗传算法的数学基础［M］．西安:西安交通大学出版社，2000．

［9］ GOLDBERG D E．Genetic algorithms in search，optimization，and machine learning．reading［M］．MA:Addison－Wesley，1989．

［10］ SOMAINI U．Binary sequences with good autocorrelation and crosscorrelation properties［J］．IEEE Trans Aerosp E-lectron．Syst，1975，AES－11:1226－1231．

［11］ 杨丽娜，丁君，郭陈江，等．基于遗传算法的阵列天线方向图综合技术［J］．微波学报，2005，21(2):38－41．

［12］ 张明友，汪学刚．雷达系统［M］．北京:电子工业出版社，2006．