3W规则有效性仿真分析

张磊，李会武，邱紫敬，滑瑞霞，郭倩，谢俊

(1.西安电子科技大学电子工程学院，陕西西安710071;2.北京市昌平自来水有限责任公司中调室，北京102200)

随着电子产品设计的高速化和小型化趋势。如何在缩小电子系统体积的同时，保持并提高系统的性能成为一个重要课题。信号频率变高，上升时间变快，印刷电路板的尺寸变小，布线密度加大等，都越来越使得串扰成为一个值得注意的问题。

1 串扰概念和分类

远端串扰电压和近端串扰电压是衡量平行微带线间串扰大小的重要指标，因此，为了计算平行微带线间的串扰，将形成串扰的电磁耦合等效为下面两幅图。

在图1(a)所示的一小段感性耦合传输线上

图1 电磁耦合等效图

近端串扰电压

同样，由图1(b)所示的一小段容性耦合传输线上，可得到

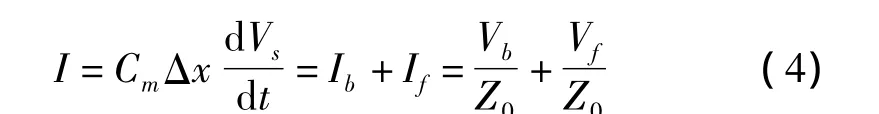
由Vb=Vf，可以得出，远端串扰电压

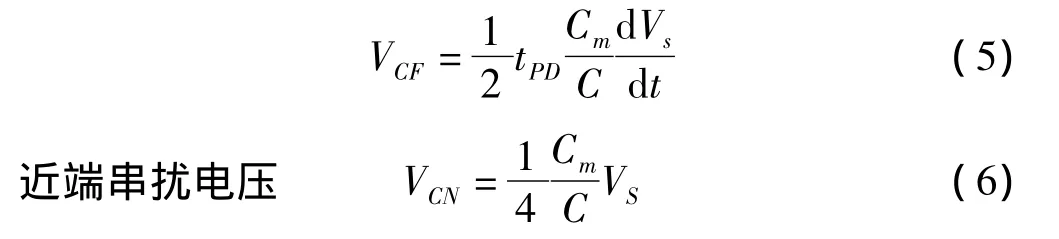
串扰电压为感性电压和容性电压之和，故总的串扰电压为

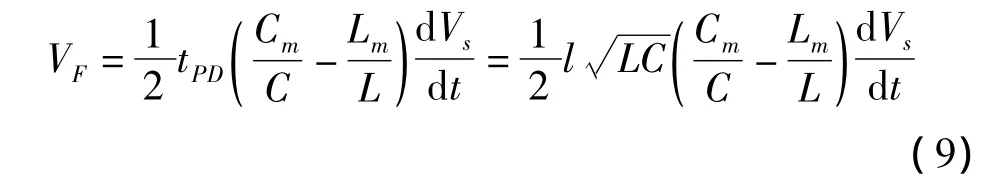
其中，l为传输线的长度;L为单位长度传输线自身电感;C为单位长度传输线自身电容。

2 仿真方法验证

为了验证该仿真方法的可靠性，选取了一组仿真结果与理论计算值进行了比较。

(1)仿真模型建立。

选取平行印制线的模型如图2所示［3］。其中，a为介质基板的宽度;w为印制线的宽度;l为印制线的长度;s为平行印制线的中心间距;h为介质的厚度;t为印制线的厚度。印制线1为干扰线;线2为受干扰线。

在HyperLynx上建立两条微带线模型［4］，如图3所示。

选取耦合微带线的参数l=100 mm，h=1.6 mm，εr=4.4，t=0.018 mm，w=3.2 mm;每个端口接匹配负载。

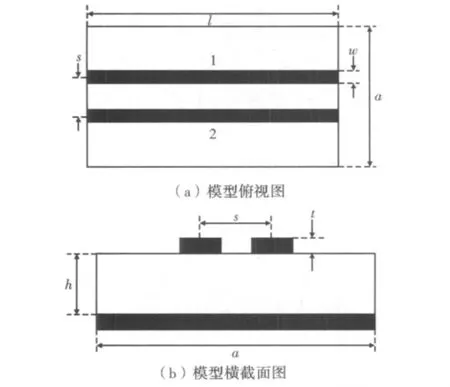
图2 平行印制线的模型

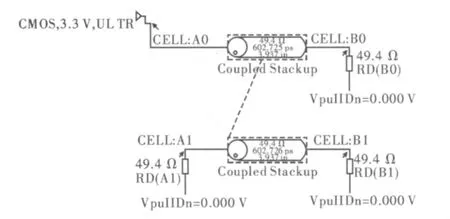
图3 HyperLynx中平行微带线的模型

(2)结果分析。

由式(7)计算得到近端串扰的理论值VN的幅值为39.3 mV。而在仿真中，当使用如图4(a)的驱动电压后，可以得到如图4(b)所示的近端串扰电压波形。从结果图4(b)可以看出:近端串扰的电压幅值约为37.89 mV，与理论计算值基本一致。因此，选取的模型和计算方法是有效的。

图4 HyperLynx仿真波形

33 W规则有效性分析

选取耦合微带线的参数l=100 mm，h=1.6 mm，εr=4.4，t=0.018 mm，w=3.2 mm;每个端口接匹配负载。

不同s时串扰计算结果如图5所示。令，即微带线的中心间距s为线宽度的n倍，也就是说n=3时，遵循3W规则。

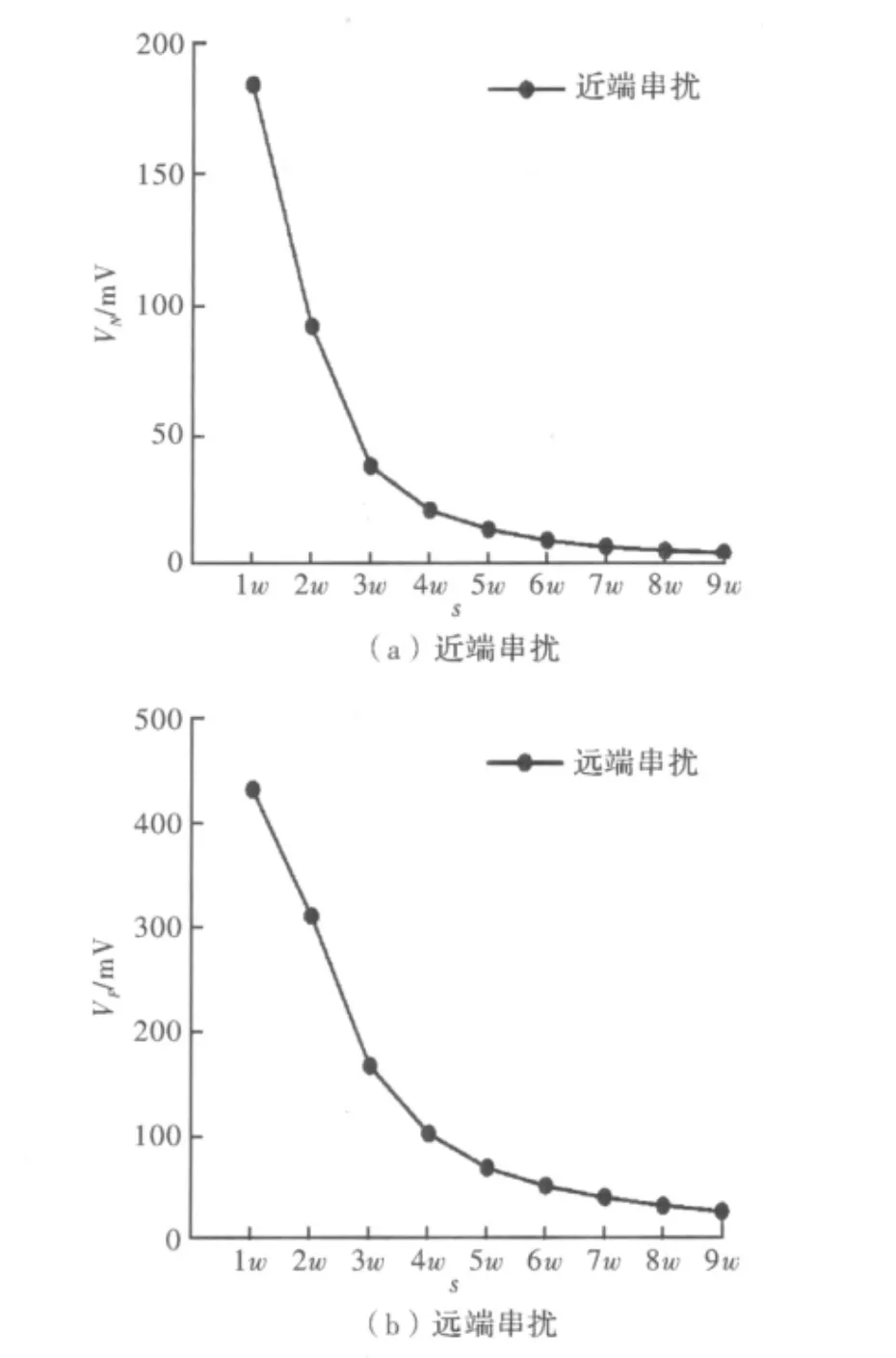
图5 不同线中心间距时的串扰

由图5可以看出，随着耦合微带线中心间距s的增大，近端串扰和远端串扰逐渐减少;微带线的中心距离＜3w时，近端串扰和远端串扰随着s的增大而急剧减少;当线中心间距＜3w时，近端串扰和远端串扰随着s的增大而缓慢减少。

这是因为s对耦合微带线之间的互感和互容的影响很大。当s增大时，单位长度互感和互容减少，而微带线自身的单位长度电感和电容不变，因此串扰随着线中心间距的增大而减少。适当增大PCB上印制线之间的距离可以有效减少串扰。从图5中可以更加清楚地看到3W规则能更好地把串扰限制在一定范围内。微带线在不受其他影响的情况下，遵循3W规则能更好地减少串扰。而为了使3W规则发挥作用，下面分析3W规则在不同线间参数条件下对减小串扰的作用情况。

4 不同线间参数条件下3W规则的有效性分析

为了验证3W规则在不同条件下对减小串扰的贡献大小，即在什么条件下，可以大幅度的降低串扰。假设线中心间距为2w时的串扰作为平行微带线的原始串扰，将其与3W时的串扰做比较，找出在哪些情况下，应用3W规则可以使平行微带线间的串扰尽可能地远低于原始串扰。因此，定义应用如式(10)所示。

其中，V3w为微带线中心间距为距为3w时的串扰幅值;V2w为微带线中心间距为距为2w时的串扰幅值。当Ψ越小时，说明应用3W规则可以使线间串扰越低，即应用3W规则的效果越好。

(1)不同线长度时的串扰和应用3W规则的效率。

选取耦合微带线的参数如下:h=1.6 mm，εr=4.4，t=0.018 mm，w=3.2 mm;s分别取2w和3w时;每个端口接匹配负载。不同时串扰的计算结果如图6所示。

图6 不同线长度时的串扰

从图6(a)可以看出，对于特定的耦合微带线结构，当微带线长度大于临界长度时，近端串扰基本稳定不变;当线长度小于临界长度时，近端串扰不能达到稳定值;线间距不同时，耦合微带线的临界长度也不同。从图6(b)可以看出，远端串扰随着线长度的增大而增大。因此为了减少串扰，PCB上的平行印制线应尽可能短。

不同线长度对Ψ的影响。

由图7可以看出，随着线长度l的增大，远端串扰的Ψ缓慢上升;而随着线长度l的增大，近端串扰的Ψ将基本保持不变。并且远端串扰的Ψ比近端串扰的Ψ要大，因而当平行印制线长度l较短时，应用3W规则能够高效地减少平行印制线之间的串扰。

(2)不同介质厚度时的串扰和应用3W规则的效率。

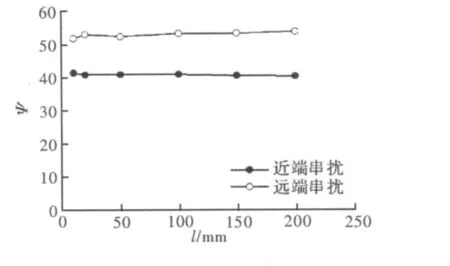
图7 不同线长度时的效率

取耦合微带线的参数εr=4.400，l=100 mm，t=0.018 mm，w=1.600 mm;s分别取2w和3w时;每个端口接匹配负载。不同介质厚度h时串扰的计算结果如图8所示。

图8 不同介质厚度时的串扰

从图8可以看出，耦合微带线的近端串扰随着介质厚度h的增大而增大;远端串扰也随着介质厚度h的增大而逐渐增大。因此减少PCB的厚度可以有效降低串扰。

由图9可以看出，随着介质厚度h的增加，近端串扰的Ψ略微下降，而远端串扰的Ψ则有上升趋势，并且远端串扰的Ψ比近端串扰的Ψ大。因此，可以看出h越小，应用3W规则越能够高效地减少串扰。

图9 不同介质厚度时的效率

(3)不同介电常数时的串扰和应用3W规则的效率。

选取耦合微带线的参数h=1.600 mm，l=100 mm，t=0.018 mm，w=3.200 mm;s分别取2w和3w;每个端口都接匹配负载。不同εr时串扰的计算结果如图10所示。

从图10可以看出，耦合微带线的近端串扰随着介质介电常数εr的增大而逐渐减少，而远端串扰随着介质介电常数εr的增大而逐渐增大。对于长线来说，远端串扰远大于近端串扰。因此从减少远端串扰的角度出发，PCB上应采用介电常数较低的介质。

由图11可以看出，介电常数εr对Ψ影响较小。但随着εr的增大近端串扰的Ψ几乎保持不变，而远端串扰的Ψ都有缓慢减小的趋势，并且远端串扰的Ψ比近端串扰的Ψ要大。因此，介电常数越大，应用3W规则能更有效地减少串扰。

图10 不同介电常数时的串扰

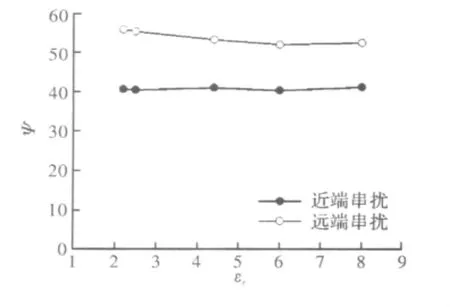
图11 不同介电常数时的效率

5 结束语

通过对PCB平行印制线的串扰仿真分析，研究3W规则的有效性。并且分析了印制电路板上平行微带线的中心边距、线长度、介质厚度和介电常数对串扰的影响。结果表明:平行微带线的中心间距s、耦合区域的线长度l、介质的厚度h以及介质介电常数εr对平行耦合微带线的串扰有很大影响。近端串扰VN随着h的增大而增大，随着s和εr的增大而减少;远端串扰VF随着l、h和εr的增大而增大，随着s的增大而减少。应用3W规则能够减少印制线之间的串扰;当线长度l较短或h较小或介电常数εr较高时，应用3W规则能有高效地减少串扰。

［1］ 李玉山，李丽平．信号完整性分析［M］．北京:电子工业出版社，2005．

［2］ 乔洪．高速PCB串扰分析及其最小化［J］．电子质量，2005(11):73－75．

［3］ SOHN Y，LEE J，PARK H．Empirical equations on electrical parameters of coupled microstrip lines for crosstalk estimation In printed circuit board［J］．IEEE Transactions on Advanced Packaging，2001，24(4):521－527．

［4］ 张海风．HyperLynx仿真与PCB设计［M］．北京:机械工业出版社，2005．