理想模型不宜运用的场景

韩静波

（浙江省路桥中学 浙江 台州 318050）

物理习题一般以理想模型开展分析，以理想模型拟合现实场景，分析解决实际问题．但有些场景会出现按照理想模型分析得出的结论和实际情况不符的矛盾．这是由于理想模型的使用是有其局限性和适用范围的．这类问题场景和理想模型的理想化条件本身存在冲突，因此不能以理想模型来求解．但此类问题场景屡见不鲜，甚至在高考题中也曾出现，导致师生分析时纠缠不清、混乱致错．如何分析和对待这类问题值得探讨．通过列举一些常见的理想模型不宜运用的场景，以引起大家关注模型的适用条件．

1 弹簧模型

【例1】（1987年高考广东卷试题）如图1，一重物m悬挂在弹簧下，再用一细绳把弹簧固定在天花板上．整个装置平衡静止后，用火烧断细绳．在绳断开的瞬间，重物m的加速度a（忽略弹簧质量和空气阻力）是

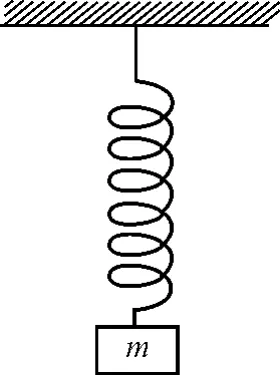
图1

A．a＜g，方向向下

B．a＝g，方向向下

C．a＞g，方向向下

D．a＜g，方向向上

答案为选项B．

当上面的细绳被烧断的瞬间，细绳对弹簧的拉力瞬间消失，弹簧的上端失去约束，弹簧瞬间恢复原状．下面重物m不再受弹力作用．所以烧断细绳的瞬间，重物m只受重力，其加速度为g，方向向下［1］．

【例2】（1999年高考上海卷试题）如图2所示，竖直光滑杆上套有一个小球和两根弹簧，两弹簧的一端各与小球相连，另一端分别用销钉M，N固定于杆上，小球处于静止状态．设拔去销钉M瞬间，小球的加速度的大小为12 m／s2．若不拔去销钉M而拔去销钉N瞬间，小球的加速度可能是（取g＝10 m／s2）

A．22 m／s2，竖直向上

B．22 m／s2，竖直向下

C．2 m／s2，竖直向上

D．2 m／s2，竖直向下

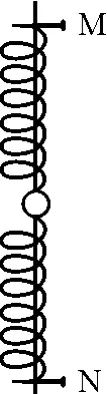
图2

答案为选项B和C．

在拔去销钉M的瞬间，对于上面的弹簧上端由于失去约束，弹簧发生长度突变，即突然恢复原状，弹力变为零．而小球由于有一定质量，具有惯性，瞬间还停留在原来的位置；下面的弹簧两端有外部条件限制，没有条件发生长度突变，所以弹力不变．拔去销钉N瞬间道理相同．

图3

【例3】（2010年高考全国卷Ⅰ）如图3所示，轻弹簧上端与一质量为m的木块1相连，下端与另一质量为M的木块2相连，整个系统置于水平放置的光滑木板上，并处于静止状态．现将木板沿水平方向突然抽出，设抽出后的瞬间，木块1，2的加速度大小分别为a1，a2．重力加速度大小为g．则有

A．a1＝g，a2＝g

B．a1＝0，a2＝g

C．a1＝0，a2＝

D．a1＝g，a2＝

答案为选项C．这是关于弹簧的弹力不能突变比较常见的一道题．

一般来说，只有当轻质弹簧两端同时受其他物体（或力）约束时，弹簧才不会发生突变．在高中阶段，轻质弹簧是不计弹簧质量的理想化模型，这在现实中是不存在的．因此关于此类理想弹簧的习题场景必须是相对有质量物体而言，才有它的相对不计的理由，而例1和例2已缺失了此先决条件，使得理想化条件被破坏，从而出现了轻弹簧突变的结果．

但笔者认为轻弹簧突变仍是不正确的，由牛顿第二定律F＝ma，由于m0，a∞，弹簧收缩所用的时间t0．而瞬间是t很小很小．这里的矛盾是瞬间是否就已经完成了收缩，能否说正收缩到一半，可否说这个瞬间太短，比很快的收缩时间还短．这里的实质是两个无穷小量的比较，哪个更小，其实难有定论．物理实际质量哪怕很小也不可能为零，故而收缩肯定需要一定时间，因此瞬间也不应该突变为零．如果这样分析，则又回到不发生突变的结论．通过这段翻来覆去的推理，笔者要阐发的意思是，这些情况下理想化条件已经出现问题，继续进行的讨论虽然符合数学逻辑，但已经不符合物理实际．在这样的前提下讨论这类习题是没有意义的．

可以从两个角度去对待这种习题：学生初学阶段避免出现；到一定程度后可以用来讨论分析．其目的是以此来认识理想化的适用条件，更加准确地把握物理这门学科理论联系实际的重要原则，切忌只进行抛弃物理实质的数学推理而得出一些似是而非的结论．

2 光线模型

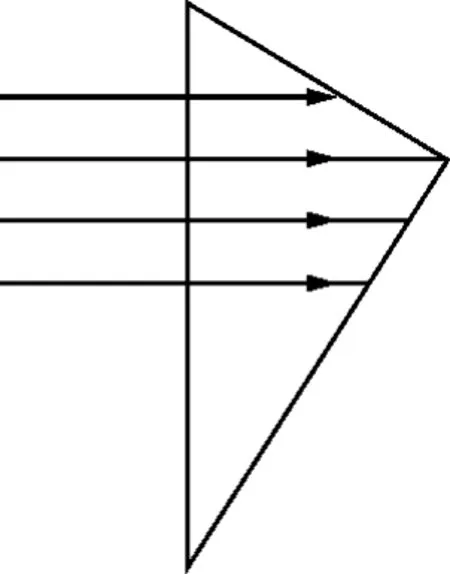
图4

【例4】如图4，水平光线射到一个直角玻璃砖上．画出光线在两条直角边上的折射、反射情况．

这是简单的习题，但问题是图4所示的第二条刚好射在直角顶点上的光线会发生怎样的折射？对此有人认为略向上一点则发生和上面光线一样的折射和反射；略向下一点则发生和下面光线一样的折射和反射；而直角位置是空缺的．另外有些人认为这一点光线发生散射．

光线是表示光的传播方向的直线，光线是一种几何的抽象，光线是不存在的，因为光是电磁波，可见光波波长为400～700 nm．把光看成线是反映光的直线传播这一性质的理想化做法，反映这一种性质的光学称为几何光学．它研究宏观层面上关于光的一些规律．实际上光具有波粒二象性，当光通过的狭缝小到1 mm左右时，光的波动性——衍射现象便显现出来．缝再小下去，光作为波的性质越显现出来．所以不能还按照光的直线传播的规律讨论光在直角顶点折射、反射问题．

3 单摆模型

【例5】如图5，细绳拴着一个圆锥形漏斗，其中装满沙子，在漏沙子的过程中，摆的周期如何变化？

图5

答案是周期先长，后短，最后复原成最初的周期．

将此装置视为单摆，其摆长为顶点到沙漏的重心位置的长度．周期先变大是因为沙子漏出去，重心降低，摆长增长；后变小是因为沙子完全漏出去后，漏斗的重心又回到几何的中心，摆长恢复为原来的长度．

以上是通常的解释．其计算结果和实验结果也相差不大．但这样处理是不妥的．历史上在研究摆的重心升降问题时，惠更斯便发现和探讨了物体系的重心问题与转动惯量问题．即考虑到重心变化的单摆已不是单摆，而是复摆．单摆的周期

而复摆的周期是

其中J为摆对轴的转动惯量，l为复摆质心到转轴的距离．

即使本题的情况与近似处理为单摆计算结果比较一致，但考虑重心升降是复摆的特性，再处理为单摆，容易造成误导．

4 质点模型

【例6】2004年雅典奥运会上，“飞人”刘翔勇夺110 m栏世界冠军．下列说法正确的是

A．刘翔在飞奔的110 m中，可以看成质点

B．教练为了分析刘翔动作要领，可以将其看做质点

C．无论研究什么问题，均不能把刘翔看成质点D．是否将刘翔看作质点，决定于所研究的问题质点是一个理想的物理模型．物体能否看成质点，关键要看所研究问题的性质．当物体的大小和形状对所研究问题的影响可以忽略不计时，可视物体为质点．本题是一个看上去十分基础的习题，但对于选项A，是否成立却有争议．当物体本身的长度远小于其运动距离时，通常可以看成质点．但在国际比赛中，短跑运动员到达终点的时刻十分接近，国际田联的规则是：在田径比赛中，所有赛跑项目参赛者的名次取决于其身体躯干（不包括头、颈、臂、腿、手或足）抵达终点线后沿垂直面为止时的顺序，以先到达者名次列前．通常的比赛都会回放录像精准分析确定名次，因此运动员是不能看成质点的．同样的110 m栏比赛，若非大赛将运动员看成质点似乎也没有关系，可方便问题研究．

为什么同样的110 m栏，有时候可以看成质点有时候不能，当没有必要考虑其形状大小时候就可以看成质点，必须要考虑其形状大小时就不能看成质点．必要和不必要有时候很清楚，但有时候却刚好是必要和不必要的过渡阶段．因此比较好的处理方式是，避免分析这类不明确的问题．

5 电容模型

对于一些带电粒子在电场、磁场及复合场中的运动，通常看起来没有问题，但只要连接成一个循环，就会发现，粒子能量可能无限增大，成了永动机．如图6所示，平行板电容器在中心处挖一个小孔，装置置于真空中，电荷不会逃走，可不考虑重力．挖了小孔后的平行板电容器内的电场分布基本不变，装置固定不动．把带正电的小球放在A处，在电场加速下到达B点，通过绝缘的光滑轨道C，绕回到A处；再次被加速，每循环一次能量增大一次，属第一类永动机．永动机是不存在的，这些粒子的能量是从哪里来的呢［2］？

我们通常认为电容器的电场只存在于两极板之间的狭窄区域，这样处理是基于电容器内部的电场远大于外部这一前提，在多数情况下，可简单处理为外部电场为零．但本问题这样处理，便出现了能量不断产生的永动机．实际上电场分布当如图7所示，电场内部，粒子从A到B，场强较大，路径较短，电场力对小球起加速作用．而通过弧︵BCA场强虽小，路径却长，电场为对小球起减速作用，两个作用的效果大小相等．电场力对从A－B－C－A的环路积分肯定为零［2］．

图6

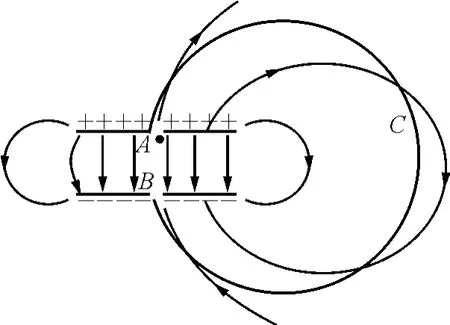
图7

6 总结

物理模型是物理规律和物理理论赖以建立的基础．模型不是实际存在的物体，它是实际物体的一种理想化的近似反映，是为了研究问题的方便而进行的科学抽象．它突出了事物的主要特征，抓住了主要因素，忽略了次要因素，使所研究的复杂问题得以简化，是一种重要的科学研究方法．但模型有其适用的条件，不能离开物理模型的适用条件绝对化地使用．物理学中的某些佯谬和错误讨论就在于没有恰当地明确适用条件．

但这类习题经常出现在辅导资料甚至高考题中．在教学中，要让学生明确理想化是一种重要的科学方法，与真实有一定差距，要注意其适用的范围和条件．

1 余良术．弹簧的弹力会发生突变吗？ 物理通报，2008（1）：61～62

2 韩静波．能量不会凭空产生．物理通报，2008（9）：18～20