基于MATLAB/Simulink转速闭环直流调速控制系统的仿真研究

钮王杰，张斌超，刘春艳

(1．运城学院机电工程系，山西运城 044000；2．阳城国际发电有限责任公司，山西晋城 048102)

直流调速系统具有调速范围广、精度高、动态性能好和易于控制等优点，所以长期以来，它一直占据垄断地位，在许多工业部门，如轧钢、矿山采掘、纺织、造纸等需要高性能调速的场合得到广泛的应用。从控制技术的角度来看，直流调速系统又是近年迅速发展的交流调速系统的基础，因而研究直流调速系统有非常重要的应用价值。MATLAB软件以其方便，快捷，高效等优点而被广泛的应用于各个领域的研究，其中Simulink平台，更是以其丰富的模块库，为各种仿真和计算提供了极大的便利[1－2]。本文以转速闭环调速系统为控制对象，采用MATLAB/Simulink平台建立系统的仿真模型，通过改变额定转速值和放大倍数的大小，来分析不同参数下直流系统的转速和转矩响应过程。

1 转速闭环调速系统的工作原理

图1 转速闭环调速系统

转速闭环调速系统的调节量是转速，所以闭环系统是在电动机轴上安装一台测速发电机TG，从而引出与转速成正比的负反馈电压Un，Un与转速给定电压比较后，得到偏差电压ΔUn，经放大器A放大后产生触发器GT的控制电压Uct，用以控制电动机的转速。这就组成了转速反馈控制的调速系统，其原理框图见图1。

系统中各环节的稳态输入输出关系如下：电压比较环节的输出为

放大器的输出为

其中，Kp为放大器的电压放大系数。

晶闸管整流器及触发装置的输出为

其中，Ks为晶闸管整流器及触发装置的电压放大系数。

晶闸管-电动机系统(V-M系统)开环机械特性为

Application of big bolting combined with anti slide pile in bedding slope support SHU Hai-ming YU Bang-jiang(88)

其中，Ce为电动机额定励磁下的电动势转速比，V·min／r；R-电枢电阻；Id为电动机电枢瞬时电流；n为转速。

转速检测环节为

其中，α2为反馈电位器分压比；Cetg为测速发电机额定磁通下的电动势转速比V·min／r；α为转速反馈系数，α ＝ α2Cetg。

直流电动机有两个独立的电路：一个是电枢回路，另一个是励磁回路。直流电动机各物理量间的基本关系式如下：

其中，U，Id为电动机电枢瞬时电压、电流；IdL为负载电流；R为电枢电阻；L为电枢电感；Te为电磁转矩；Km为转矩常量；TL为负载转矩；Cm为电动机额定励磁下的转矩电流比N·m／A。

其中，Ce为电动机额定励磁下的电动势转速比，JG为转速惯量，

其中，GD2为电力拖动运动部分折算到电动机轴上的飞轮惯量。

2 转速闭环系统的数学模型

根据图1各环节的稳态输入输出关系，可画出转速负闭环调速系统的控制结构图，如图2所示。

图2 转速负反馈单闭环调速系统稳态结构图

图2中各方块的符号代表该环节的放大系数，也称传递函数。由以上各关系式中消去中间变量，得到系统的静特性方程式为

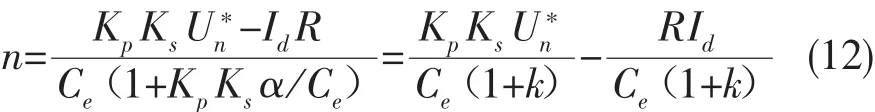
其中，K为闭环系统的开环放大系数，K＝KpKsα／Ce。

电动机转速降为

该系统在电动机负载增加时，转速将下降，转速反馈Un减小，而转速的偏差ΔUn将增大，见(1)式。同时放大器输出Uct增加，并经移相触发器使整流器输出电压Ud增加，电枢电流Id增加，从而使电动机电磁转矩增加，转速也随之升高，补偿了负载增加造成的转速降。

从稳态特性方程可以看到，如果适当增加放大器的放大倍数Kp，电动机的转速降Δn将减少，电动机将有更硬的机械特性，也就是说，在负载变化时，电动机的转速变化将减少，电动机有更好的保持速度稳定的性能。如果放大倍数过大，也可能造成系统运行的不稳定。

图3 转速负反馈有静差直流调速系统仿真模型

3 仿真分析

根据直流调速系统的组成，建立其Simulink仿真模型如图3所示。设置仿真时间为1．5 s，电动机空载起动，起动 0．5 s后加额定负载 TL＝171．4 N·m 。

直流电机的参数为如下[3－6]：

电枢电阻 Ra－ 0．21 Ω；电枢电感 Ld－ 0．00021 H；励磁电感 Rf－0 H；励磁电阻 Rf－146．7 Ω；磁场与电枢互感 Laf－0．84 H；转动惯量 J－0．57kg m2。

由仿真响应曲线图4～7可以看出，在全电压直接起动情况下，起动转矩最大，在0．25 s左右起动转矩下降为零 (空载起动)，起动过程结束，这时电动机转速上升到最高值。在起动0．5 s后加额定负载，电动机的转速下降，转矩增加，并随着时间的推移，转矩和转速响应均趋于稳态值。由图4、图5可以看出，当额定转速U*n=10时，放大倍数KP由10变为200时，系统在启动结束后，稳态转速提高，即稳态转速降减少，转速、转矩达到平稳值的时间变短，而且过度过程平稳，系统响应较好。由图6、图7可以看出，当转速降为额定转速一半即时，放大倍数KP由10变为200时，系统在启动结束后，系统的稳态转速提高即稳态转速降减少，转速、转矩达到平稳值的时间变长，而且响应过程振荡强烈，过度时间长，但转速还是稳定的，这是转速闭环调速系统中所用晶闸管整流器控制输出电压只能在0-Udmax范围内变化，尽管放大倍数很高，转速还没有出现严重的不稳定现象。

图4 =10，KP=10时转速、转矩响应曲线

图5 =10，KP=200时转速、转矩响应曲线

图6 =10，KP=10时转速、转矩响应曲线

图7 =10，KP=200时转速、转矩响应曲线

4 结论

本文以MATLAB/SIMULINK为平台，建立转速闭环直流调速系统的仿真模型，通过改变额定转速和放大倍数两个参数，来观察不同参数下系统转速、转矩响应过程。仿真结果表明：在不同的额定转速和放大系数的作用下，转矩和转速响应过程快速性、平稳性及稳态性能都比较好，系统的参数设计满足要求。

[1]陈伯时．电力拖动自动控制系统[M]．北京：机械工业出版社，2004．

[2]姚建红，戴琳，厉立国．基于Matlab/Simulink的双闭环直流系统的设计[J]．佳木斯大学学报，2006，24(4)：521-523．

[3]刘晓梅，李洪友．应用IGBT的直流调速系统的设计与研究[J]．组合机床与自动化加工技术，2 006，6(3)：64-66．

[4]徐月华，汪仁煌．Matlab在直流调速设计中的应用 [J]．微计算机信息，2003，19(8)：32-33．

[5]万里光．基于Matlab的双闭环直流电机调速系统的仿真[J]．船电技术控制计术，2011，31(2)：30-32．

[6]洪乃刚．电力电子、电机控制系统的建模与仿真[M]．北京：机械工业出版社，2010．