数码相机定位系统中系统标定模型*

张吉昕 甄 平

(黄石理工学院数理学院,湖北黄石 435003)

0 引言

数码相机定位是指用数码相机摄制物体的相片,确定物体表面某些特征点的位置。最常用的定位方法是双目定位,即用 2部相机来定位。用 2部固定于不同位置的相机摄得物体的像,分别获得该物体上的特征点在 2部相机像平面上的坐标。只要知道 2部相机精确的相对位置,就可用几何的方法得到该特征点在固定一部相机的坐标系中的坐标,即确定了特征点的位置。对于双目定位,精确地确定 2部相机的相对位置是关键,这一过程称为系统标定[1]。

1 靶标上的点到像平面的映射模型

1.1 数码相机的几何模型

在建立模型之前假设相机拍照时,不受周围环境(如温度、湿度等因素)的影响;假设该相机的成像原理符合针孔成像原理;假设该相机焦距等于 1倍相距(数码相机中相距在 1～2倍焦距之间)[2]。

数码相机的图像拍摄实际上是一个光学成像过程。根据成像原理可以将此分为 3个步骤,隶属于 4个坐标系,这 4个坐标系分别为:

1)世界坐标系——根据自然环境所选定的坐标系,因为靶标是在一个平面上,坐标值用(Xw,Yw)表示。

2)图像坐标系——坐标原点在 CCD图像平面的中心,X轴、Y轴分别为平行于图像平面的2条垂直线,坐标值用(u,v)表示。

3)像素坐标系——坐标原点在 CCD图像平面的左上角,X轴、Y轴分别平行于图像坐标系的X轴、Y轴,坐标值用(u,v)来表示,且为离散的整数值。

4)光心坐标系——以相机的光心为坐标原点,X轴、Y轴分别平行于图像坐标系的 X轴、Y轴,相机的光轴为Z轴,坐标值用(Xc, Yc,Zc)表示。由于靶标是二维图,所以光心坐标系只取 X、Y轴坐标建立与其他坐标系的二维映射关系。

为了能够确定光心坐标系与靶标(世界坐标系)之间的映射关系,首先要建立图像坐标系与靶标(世界坐标系)之间的映射关系。为了能使模型更加精确,还要建立一个由图像坐标系到像素坐标系的转换关系,从而得到像素坐标系与靶标坐标系之间的映射关系。最后得到光心坐标系与靶标坐标系之间的映射关系。

1.2 数模相机的标定过程

这一成像过程可分 3个步骤完成,3个步骤分别将世界坐标系中的信息转换到光心坐标系,再由光心坐标系转换到图像坐标系,最后由图像坐标系转换到像素坐标系。

光学成像的理论模型是针孔模型。根据这个模型由光心坐标系向图像坐标系转换过程符合中心影射或透视影射,可用齐次坐标与矩阵表示:

其中,(Xc,Yc)是光心坐标系中一空间点P的坐标,(x,y)是对应图像坐标系中P点的坐标,f是拍摄相机的焦距。由世界坐标系到光心坐标系的转换关系为:

其中,R是旋转矩阵,t是位移向量。

为了能使模型更加精确,需要建立一个由图像坐标系到像素坐标系的转换关系:

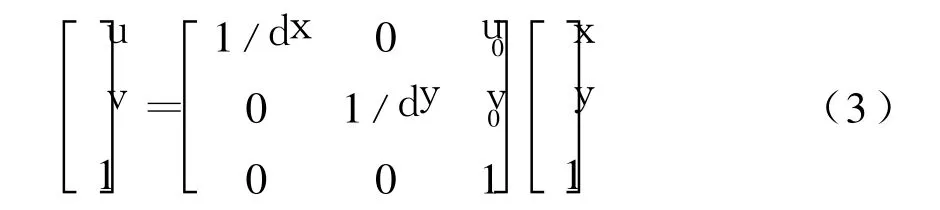
其中,(u0,v0)是坐标系原点在像素坐标系中的坐标,dx,dy分别是像素坐标系在 X方向和Y方向相邻像素间的距离。将式(1)、式(2)代入式(3)得:

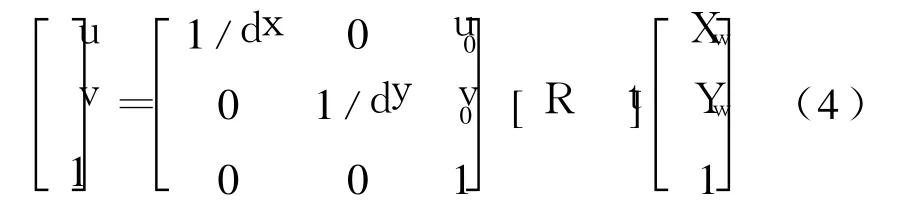
可将式(4)简化为:

N为式(4)右边第 1项,称为内部参数矩阵,显然 N为满秩矩阵,当相机的参数已知时,N是已知的。M为式(4)右边第 2项,称为相机的外部参数,Q称为投影矩阵。式(5)即为模型。

由M=N-1Q可计算光心坐标系与靶标之间的映射关系:

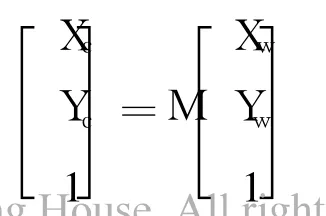
2 实验

2.1 利用实验数据求解模型

在一块平板上画若干个点,同时用2部相机照相,分别得到这些点在它们像平面上的像点,利用这 2组像点的几何关系就可以得到这2部相机的相对位置。然而,无论在物平面或像平面上我们都无法直接得到没有几何尺寸的“点”。实际的做法是在物平面上画若干个圆(称为靶标),它们的圆心就是几何的点了,而它们的像一般会变形,所以必须从靶标上的这些圆的像中把圆心的像精确地找到,标定就可实现。有人设计靶标如下:取 1个边长为100mm的正方形,分别以4个顶点(对应为A、C、D、E)为圆心,12 mm为半径作圆。以AC边上距离A点30 mm处的B为圆心,12 mm为半径作圆,如图 1所示。用一位置固定的数码相机摄得其像,如图 2所示。

图1 靶标示意图

图2 靶标的像

通过计算机编程软件 VB在图像上以图像的左上角为坐标原点建立 u-v坐标系,分别作出靶标上 4个圆的 8条公切线,并得出切线两两相交的 16个交点(图 3)在像上的坐标(由于 2条相交切线的交点从靶标映射到像上时还是该点,因此取这些交点及其对应点作为参考对象),再根据图像的尺寸5 625mm× 3 690 mm和图像的像素尺寸1 024×768,计算出它们在像素坐标系下的坐标,见表 1。

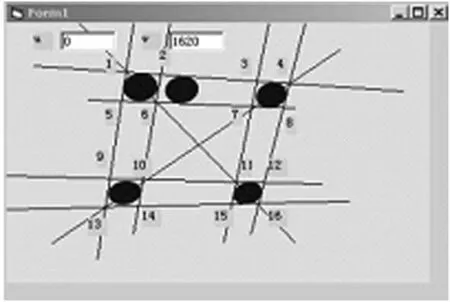
图3 靶标上点在像素坐标系下的坐标

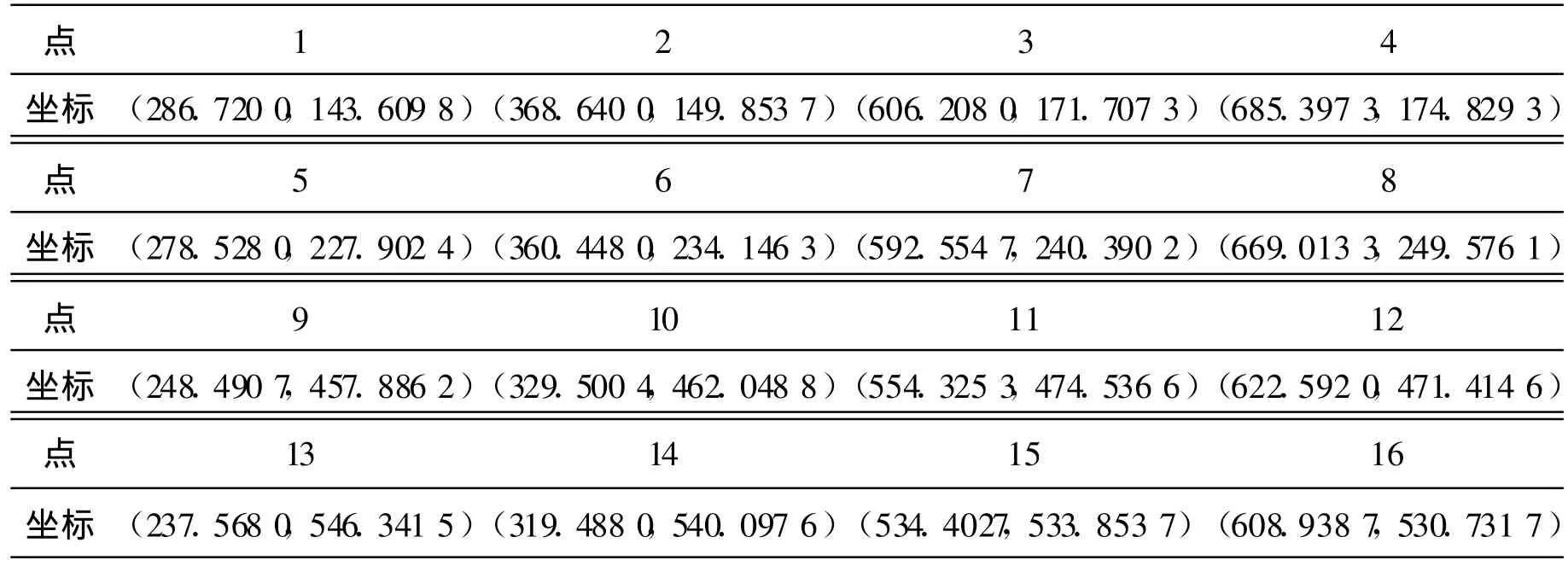
表1 切线两两相交的16个交点在像素坐标系下的坐标 (单位:像素)

以靶标上第 1条横向共切线与第 1条纵 向共切线的交点作为坐标原点,以 AC方向作为X轴方向,以AE方向作为Y轴方向建立世界坐标系。分别作 4个圆的 8条公切线,并模拟出两两相交的切线的 16个交点在像上的坐标如表 2所示。

表2 两两相交的切线的16个交点在像上的坐标(Xw,Yw) (单位:mm)

现用相机参数:像距是1 577个像素单位(1mm约为 3.78个像素单位),根据假设,这里取焦距等于 1倍像距,相机分辨率为1 024× 768,可求得:

根据以上 16个点的对应坐标,拟合得到矩阵Q,再由M=N-1Q利用Matlab计算出M:

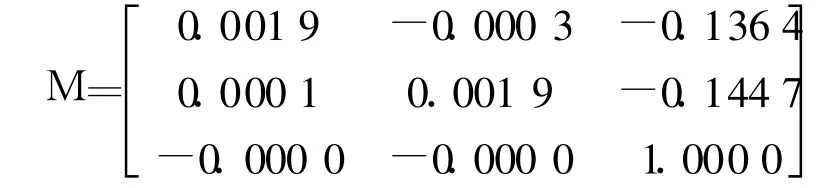
代入靶标上圆的世界坐标:A(12,12)、B (42,12)、C(112,12)、D(112,112)、E(12, 112),通过计算模型计算出它们在像上的像素坐标,再根据式(3)计算出它们的图像坐标如表 3所示。

表3 图像坐标

2.2 对结果进行误差分析

针对模型分别取对角线交点、A圆的上切点、A圆的下切点、B圆的上切点、B圆的下切点。通过计算|ΔX|=|计算值 -测量值|, |ΔY|=|计算值-测量值得出计算值与测量值之间的绝对误差如表 4所示。

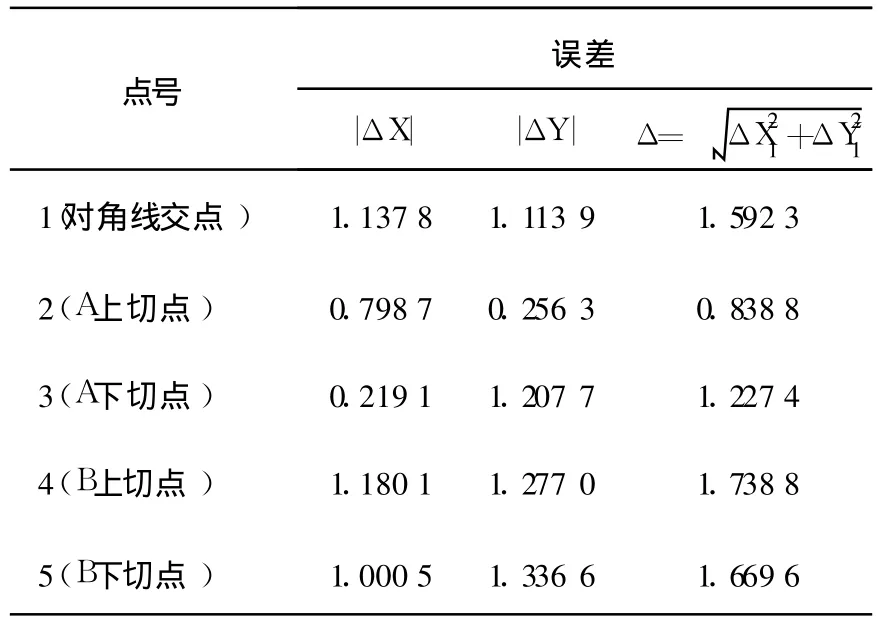
表4 计算值与测量值之间的绝对误差

靶标上若干点a,b,c,d,e,……,可以找到在其像上的对应点,分别计算出 ΔX、ΔY,运用Matlab分别进行数据拟合得到Xw、Yw与误差的函数关系f(Xw)、f(Yw)。最终靶标映射到像上的点坐标为(u-f(Xw),v-f(Yw)),从而达到减小误差的目的。

通过分析,产生误差的原因如下:

1)由于像上圆的切点坐标不容易精确标定,故在求|ΔX|和|ΔY|时可能会出现误差。

2)计算机在进行图像处理时是以像素为单位的,而在像空间坐标系中通常采用标准长度(例如m,mm)。如式(1)所示,物方单位(x,y,z)和焦距f以标准单位表示,而像方几何量(x,y;x0,y0;Δx,Δy)以像素为单位表示,比较简单,这样就在像素和标准单位的相互转换中产生误差。

3)模型是使像的所有量均以像素为单位,这样对系统误差改正数,也要以像素表示。通常数码相机在 X,Y方向上像素 dx和 dy的大小是一样的,但也存在加工过程的误差造成在X,Y方向上像素的 dx和dy大小不一致的现象。

3 结束语

本文利用数码相机采集图像的参数时,根据相机成像原理建立模型,完成数码相机的标定。该模型确定参数时只用引入相片上的参数,而不必引入具体的数码相机本身参数,所以简单、容易操作,比较通用。实验表明了这种方案的可行性,且具有一定的标定精度。

[1] 姜大志,孙闵,刘淼,等.数码相机标定方法研究[J].南京航空航天大学学报,2001(1):55-59

[2] 金刚,李德华,蔡涛,等.双相机结构光系统中两机定标与映射计算[J].华中科技大学学报:自然科学版,2002,30(10):62-64