关于复对数性质的一个问题的探讨
李明泉
(三峡大学理学院,湖北宜昌 443002)
复对数函数是实对数函数在复数域内的拓广,拓广后的复对数函数既保持了实对数函数的一些基本性质,同时又获得了一些新的特性,这是在教学中应该特别提醒学生的.例如,设z1,z2是不为 0的复数,则:
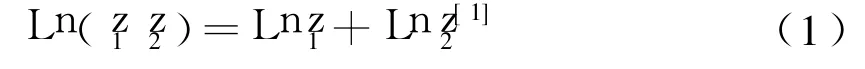
式(1)在复数范围内仍成立.由于复对数函数是无穷多值函数,因此式(1)要理解为等式两端值的全体是相同的,即对式(1)左端的任一值,在式(1)右端都可以找到一值与之相等,反之亦然.
设z是不为0的复数,考虑等式:

容易看出式(2)在复数范围内不再成立.
式(1)还可以加以推广,设复数 zi≠0 (i=1,2,…,n),则:
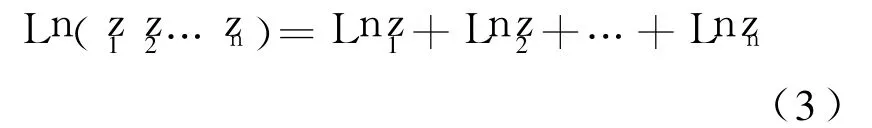
特殊的,当zi=z≠0(i=1,2,…,n)时,式(3)成为:
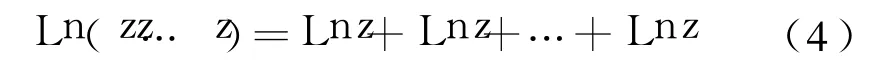
显然式(4)可记为:
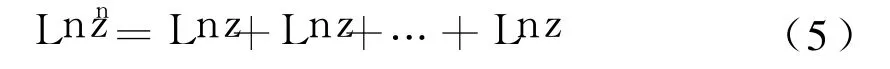
值得注意的是式(5)右端不能记为:
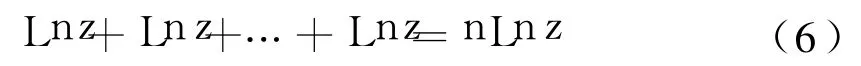
否则式(5)成为式(2),因此式(6)在复数域内是不成立的.再举一个具体例子来说明式(6)不成立,例如,取z=1,当n=2时,由式(6)得Ln1+Ln1=2Ln1[2],即:In|1|+ i(arg1+2kπ)+In|1|+i(arg1+2mπ)=2[In |1|+i(arg1+2nπ)],也就是2kπi+2mπi= 4nπi(其中k,m,n为整数),当k=0,m=1时,左端的值为 2πi,显然不存在整数 n的值,使得2πi=4nπi.
由于Lnz的主值Inz=In|z|+iargz为一单值函数,因此式(6)对主值Inz是成立的,即:
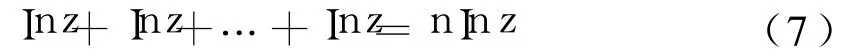
通过以上的分析可以得出结论:式(6)在复数域内不成立,而式(7)是成立的.
1 对一个证明的不妥之处的纠正
由西安交通大学高等数学教研室编写的《复变函数》(第 4版)是目前较流行的一本工科复变函数教材,很多高校都把该教材作为工科专业的教科书,该书在讲授 a与 b的乘幂ab=ebLna时指出:当a是不为0的复数,而b为正整数n时,a与b的乘幂就是通常意义的 a的n次幂,即an=a·a…a,其证明如下:
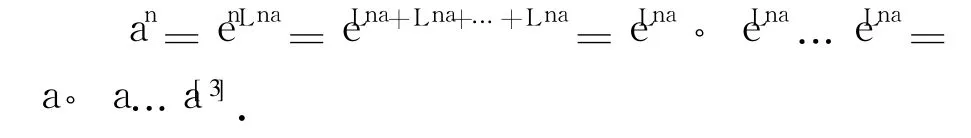
该证明过程显然用到了式(6),这是不妥当的,很容易让读者误认为式(6)是成立的,比较合理的证明为:an=enLna=en(Ina+2kπi)= enIna+2knπi(其中 k为整数).由于复变指数函数是以 2πi为周期的周期函数,因此有 an= enIna,再由式(7)得:
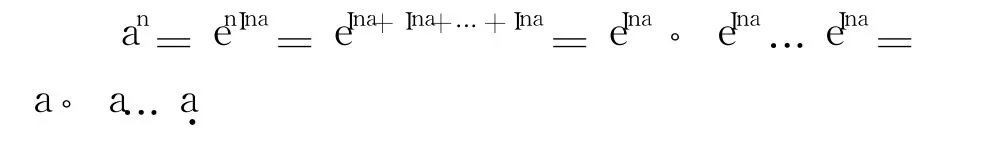
[1] 钟玉泉.复变函数学习指导书[M].北京:高等教育出版社,2004
[2] 余家荣.复变函数[M].北京:人民教育出版社, 1979
[3] 西安交通大学高等数学教研室.复变函数[M]. 4版.北京:高等教育出版社,2003

