基于十六矩阵的新型绝对式多圈光电编码器
时伟,丁洪昌,曹国华
(长春理工大学 机电工程学院,长春 130022)
光电轴角编码器基于光电检测原理,是非接触角度测量领域中一种应用广泛的传感技术,在传感器测量领域有着不可比拟的地位。根据编码方式的不同[1],大体可分为增量式、绝对式和准绝对式光电编码器三大类。其中绝对式光电轴角编码器具有绝对零点、绝对位置测量、断电信号不丢失、测量可靠性高、无累计误差等优越性,与多圈测量方式相结合,可实现直线位移、电机转速、大量程角度的精确测量,应用于智能机器、遥控、自动测量等各个行业,受到了广大使用者的青睐。
为了实现绝对式编码器的高可靠性、高精度、小型化、大量程测量,本文设计了基于十六矩阵的矩阵码编码方法,通过读数头位置的选择,2圈码道实现了19位信息的编码。其中第一圈实现了高4位格雷码,第二圈实现了低15位格雷码,该码盘构造极大的缩小了码盘空间。配合组合式机械传动结构,采用齿轮直接读圈计数方法,实现了16圈计数,多级扩展,大量程测量的功能。下面就其码盘编码、读数头放置及译码原理,多圈机械传动结构及齿轮读圈方法进行详细介绍。
1 十六矩阵码盘设计

图1 12位四矩阵编码器码盘图案Fig.1 Twelve bit and fourmatrix encoder disc design

图2 四矩阵粗码狭缝图案Fig.2 Four-matrix C/A code slit pattern

图3 11位八矩阵码盘器粗码码盘图案Fig.3 Eleven bit and eightmatrix encoder disc design

图4 八矩阵粗码狭缝图案Fig.4 Eight-matrix C/A code slit pattern
矩阵式码盘设计的编码原理是根据格雷码的编码规则,将码盘圆周划分为若干个扇形区域,每一个区域上根据位数关系,将几个不同位数的码道刻划在同一圈内,与狭缝盘相配合,将光电读数头接收到的电信号,经过放大比较、细分、译码、校正等信号处理电路转化成表征码盘旋转位置信息的自然二进制码,进而获得对应的绝对角度[2]。
目前广泛应用的矩阵式光电编码器大多为四矩阵、八矩阵编码盘[3],如图1 图4所示,将码盘圆周划分为4或8个区间,可以同时将四位、八位码道刻在同一圈上。
根据矩阵码道的编码方式[4]及应用结构,设计十六矩阵编码方式的码盘图案如图5所示,其中2为各扇形区域的刻线数。

图5 十六矩阵码盘图Fig.5 Sixteen-matrix encoder disc design
码道展开图如图6所示。码盘刻划规则:设计刻划两圈码道,实现粗码19位分辨率。内圈码道均分透光和不透光两个区域:0°~ 180°为通光区(亮区),180°~360°为不通光区;外圈码道以22.5°为间隔划分为16个扇形区间,从0°逆时针方向依次记为第1、2、…、16区,包含15位不同周期码值。其中 1区设计成 0°到 45°之间,11.25°到 22.5°之间为通光区,其余各区均按照矩阵编码的方式进行。
编码盘需要与相应的狭缝盘配合构成光栅副结构,才能精准定位。狭缝布局分内外两圈,内圈设置8个狭缝,从0°开始间隔45°依次排列,分别用标记;外圈设置16个狭缝,从0°开始间隔22.5°依次排列,分别用1,2,…,16标记,可以得到16路电信号,且每路信号包含15种不同周期的信息。

图6 十六矩阵码道展开图Fig.6 Sixteen-matrix encoder disc expansion view
2 信号处理
由粗码狭缝得到的19路电信号需经过放大、比较整形、译码、校正[5]、显示等环节,得到表征位置信息的自然二进制码及角度值。其传统电路与矩阵式绝对式编码器的部分相类似,不再详述,其中译码电路相对复杂,由狭缝内外圈得到的格雷信号如表1所示。

表1 内圈8狭缝获得码道信号Tab.1 Code channel signal from inner ring eight slit

表2 外圈16狭缝获得码道信号Tab.2 Code channel signal from outer ring sixteen slit
内圈8路信号中,A表示通光区域,与格雷码编码关系为:
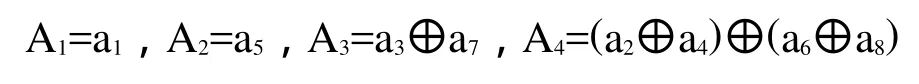
外圈16路信号如表2所示。
表中各位均不是单一周期的二进制格雷码,需根据译码原理[6],通过内圈码道 A1、A2、A3、A4将单周期信号分别分离出来。得到16路单周期信号与二进制码的关系为:

按照上述公式组(1)译码后,得到19位粗码道信号。扩展外圈可刻划2条精码道,2条校正码道,对径相加后,经单片机细分,选取适当的插补系数,得到准精码信息,通过校正码校正处理后与粗码共同构成高精度单圈角度测量值。

3 多圈传动原理及实现
传统的多圈光电轴角编码器通常采用双码盘结构[7],一个用于标记单圈角度信息,一个用于记录主轴转过的圈数。或者采用多单圈编码器组合测量多圈的系统测量方法,结构相对复杂。本设计两级齿轮传动系[8],通过末级齿轮与狭缝架组合结构,获得圈数的绝对信息,实现多圈绝对测量。二级齿轮组传动如图7所示。
采用二级齿轮组结构,选用相同的小齿轮 14齿,大齿轮28齿,模数为0.5的传动结构,两级传动,24=16系统传动比为 1:16,当主轴转过 16圈时,II末级齿轮转过1圈。通过简单译码电路及校正关系,可以实现多圈精确测量。其末级齿轮结构如图9所示。

图7 二级齿轮组传动结构示意图Fig.7 Two-stage gearing structure diagram
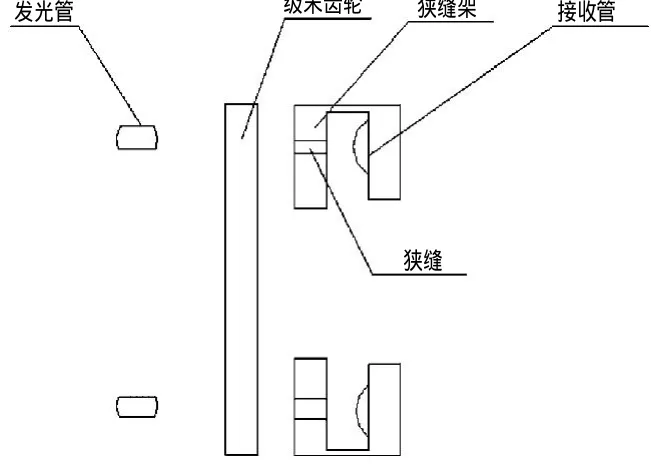
图8 读圈结构原理图Fig.8 The structure diagram of obtaining number of turns
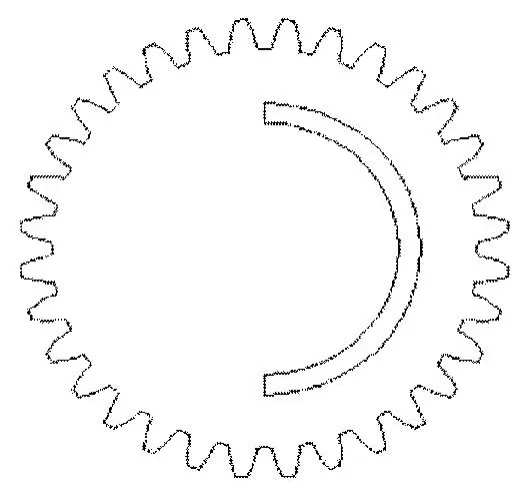
图9 末级齿轮图案Fig.9 Last stage gear design
每一组末级齿轮的狭缝架上间隔90°的双狭缝输出2位圈数信息,可记录16圈信息。通过齿轮与狭缝架的叠加信息,经译码,校正处理后,即可得到相应的圈数。
4 结论
十六矩阵码盘设计2圈粗码道,经译码可得到19位粗码的位置信息,加上精码细分、校正后高位码值,为矩阵式光电轴角编码的高精度、小型化提供了一种新的方法,具有巨大的理论和应用价值。
多圈测量方式采用二级齿轮传动的组合式结构,通过各级末端齿轮上狭缝架得到的多圈绝对位置的计数,该齿轮计数装置可实现分级计数,多级扩展,可以单圈编码器分离配合使用,通过对齿轮个数及齿轮组数的增减,实现多圈圈数的计量。该思想为多圈编码器的发展提供了新的方法,具有较好的市场前景。
[1]董莉莉,熊经武,万秋华.光电轴角编码器的发展动态[J].光学精密工程,2000,8(2):199-202.
[2]叶盛祥.光电位移精密测量技术[M].成都:四川科学技术出版社,2003.
[3]刘长顺,王显军,韩旭东,等.八矩阵超小型绝对式光电编码器[J].光学精密工程,2010,18(2):326-333.
[4]曹振夫.小型绝对式矩阵编码器[J].光学机械,1985(5):66-70.
[5]苏海水,刘恩海.单圈绝对式编码器的研制[J].光学精密工程,2002,10(1):74-77.
[6]Matszoe Y,Yoshizawa T.High-performance absolute rotary encoder using multi-track and M-code[J].Opt Eng,2003,42(1):122-130.
[7]赵志巍,陈赟.一种基于金属码盘的新型绝对式光电轴角编码器[J].传感器技术学报,2010,23(5):655-659.
[8]赵传威.一种三轴联动多圈编码器的研制[J].长春理工大学学报:自然科学版,2009,32(1):8-10.

