数学史在中学数学教育中的价值体现

亥仁古力·麦麦提

(喀什师范学院数学系,新疆喀什844008)

好的开头是上好一节课的基础,学生往往认为数学课枯燥乏味,若老师课堂开头平平而起,必然不能引起学生听课的兴趣.就培养学生的数学思维能力而言,前人数学思维发展中的经验教训是最有借鉴意义的,是因为数学知识不会离开数学史而凭空产生.为此,数学教育应当努力还原,再现这一发展过程,从数学家的废纸篓里寻找知识的源泉.因此,数学史是数学教学的重要内容,也是培养数学能力和实施数学素质教育的关键所在.《全日制义务教育数学课程标准 (试验稿)》的一个特色就是明确的将“数学思考、解决问题、情感与态度”列为课程目标,学生通过数学文化的学习,了解人类社会发展与数学发展的相互作用,认识数学发生、发展的必然规律;了解人类从数学角度认识客观世界的过程;发展求知、求实、勇于探索的情感和态度;体现数学的系统性、严密性、应用的广泛性,了解数学真理的相对性,以此来提高学习数学的兴趣.数学史对实现新课程的整体目标将发挥重要的、不可替代的作用.所以,不管是中学教师还是大学教师都要在教学中注意发挥数学史与数学教育的价值.

1 数学史在数学教育中可以开阔学生视野,培养数学学习兴趣

数学史和数学教学息息相关,在课堂教学中渗透数学知识,可以开阔视野,培养学生学习数学兴趣,展现人格魅力.就大多数学生而言,与其他学科相比,数学是较抽象、枯燥和乏味的,他们可能不知数学是一门历史性或者说积累性很强的学科.重大的数学理论总是在继承和发展原有理论的基础上建立起来的,它们不仅不会推翻原有的理论,而且总是包容原来的理论.比如,小学时学了整数,到初中阶段就先后发展到有理数和实数,最后在高中又发展到复数,而数的每一次扩展都不会推翻原来的数的运算法则,而是包含了原来的法则,这就是“数的扩张的一致性”.而其他自然科学都不乏后来的理论推翻以前理论的例子.由此可以看出,数学有不同于其他学科发展的独到之处,这也许是数学被称为基础科学而不是自然科学的一个原因.鉴于数学的这一特点,一百多年前,德国的数学史家汉克尔 (H.hankel,1839-1873)形象地指出数学与其他自然科学的显著差异：“在大多数的学科里,一代人的建筑为下一代人所摧毁,一个人的创造被另一个人所破坏.惟独数学,每一代人都在古老的数学大厦上添加一层楼.”尽管汉克尔的话有些绝对,但还是形象地指出了数学这门学科的积累特性.从这个意义上说,不了解数学史就不可能全面了解数学科学.

为了全面了解数学科学、探索数学发展的规律、数学教育的目的,都应该开展数学史的教学与研究.研究与学习数学史,可以弄清数学发展过程中的基本史实,再现其本来面貌,同时透过这些历史现象对数学成就、理论体系与发展模式做出科学合理的理解、说明与评价,进而探究数学科学发展的规律与文化本质,帮助我们掌握数学的概念、思想、方法和理论,认识数学科学与人类社会的互动关系,以及研究数学思想的传播与交流史.

2 中学生对数学史认识水平的素养调查与分析

数学史是数学教学的重要内容之一.随着新课程在全国的推进,数学史和数学文化教育正日益受到教育部门的重视.但是,从当前的中学数学教学现状来看,数学史教育并没有得到很好的推广.很多数学老师在进行数学教学时,经常把有关的数学史知识一带而过,或干脆不讲,这就大大忽视了数学史对中学数学教学的促进作用;虽然有些教师能够经常性地进行数学史教育,但他们也仅仅停留在介绍数学家的故事这个教育层面上,很少从文化价值的角度去挖掘数学史的教育价值.为了了解中学生对“数学与数学史”的兴趣,笔者曾在喀什第一、第三、第六中学112名学生中作了一次问卷调查.对这次调查的结果和问题分析如下.

(1)你们数学老师在课堂中是否讲过关于数学史方面的知识、数学家的故事对你学习数学有促进作用吗?

A.经常讲 14.2%;B.有时讲 66.1%;C.没有讲过 19.7%

(2)如果数学老师给你讲关于数学家的故事,你喜欢听吗?

A.喜欢 74.4%;B.不喜欢 12.5%;C.认为浪费时间 13.1%

(3)你喜欢读课本上关于数学家的故事吗?

A.喜欢 61.7%;B.不喜欢 13.3%;C.认为浪费时间 7.2%;D.没读过 17.8%

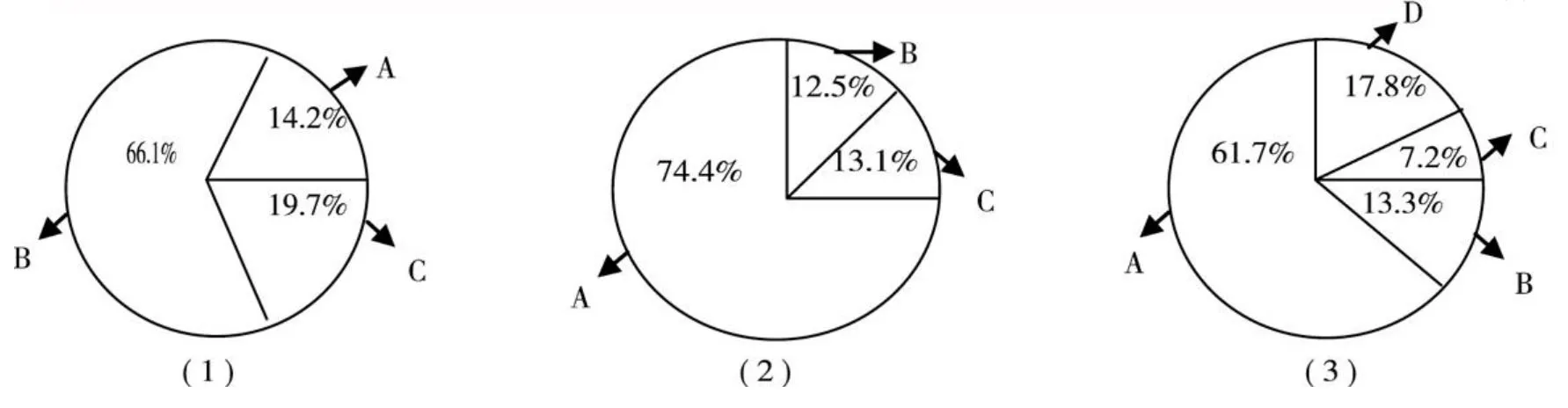
图1 学生对“数学与数学史”兴趣调查统计图

上述调查结果表明：很多数学老师在课堂上偶尔把数学史内容穿插在课堂上讲解,而大部分学生比较喜欢倾听和阅读关于数学家的故事.通过访谈记录,学生们认为,如果老师能在数学课程中对学生介绍有关数学史、数学家的故事能促进他们对学习数学的兴趣,并希望老师在课堂上能多介绍一些数学史知识、数学家的故事.通过挖掘数学史的文化价值进行教学,让数学文化的魅力真正渗入教材、到达课堂、溶入教学时,数学就会更加平易近人,数学教学就会通过文化层面让学生进一步理解数学、喜欢数学、热爱数学.因为,数学史对于揭示数学知识的来源和背景,对于引导学生体会真正的数学思维过程,创造一种探索与研究的数学学习气氛,激发学生对数学的兴趣以及培养探索精神和审美能力都有重要意义.

3 新课标指导下运用数学史进行数学教学的对策

如何运用数学史教学是国际数学教育界共同关心的问题.新课程指出：“数学文化应尽可能有机地结合数学课程的内容,选择介绍一些对数学发展起重要作用的历史事件和人物,反映数学在人类社会进步,同时也反映社会发展对数学发展的促进作用.”也就是说,要求数学教学充分反映数学的文化底蕴,从课程内容、概念形成、证明方法、习题配置等各个方面,全方位地将数学史溶入,丰富和促进数学教学.

3.1 运用数学史导入新课

运用数学史进行教学可以采用多样化的教学方式,例如教师可以在导入新课时介绍有关的文化背景;适当的介绍数学家的思想方法等有意识地强调数学的德育价值,贯穿思想品德教育.这样才能达到教学效果,更好地体现新课程精神.运用数学史导入新课可以吸引学生,激发兴趣,让学生了解相关知识的来胧去脉.

案例 (1)在讲等比数列的时候就可以出这样一道题：1420年元宵节的傍晚,浙江杭州市城内外灯火齐明,到处是一派欢乐的节日气氛,在钱塘江的一座亭子里,几位书生对着倒映在江水中五彩缤纷的美丽灯色,一边开怀畅饮,一边轮流吟诗,轮到一位少年时,他腼腆地笑了笑说：“诸位仁兄诗才横溢,妙句连篇,小弟也就不再班门弄斧”,另吟一首诗请听：“远望巍巍塔七层,红光盏盏倍加增.共灯三百八十一,试问塔顶几盏灯?”大伙听后,连连称赞,并一起注目仰望前方白塔岭上那座用灯点缀着的七层白塔,深思良久,却无人能算出答案,这位少年详细讲解后,大家才恍然大悟,大家一起举杯向他称贺,祝愿他将来在数学上取得更辉煌的成就.这位少年就是吴敬,在后来的几十年中,他果然不负众望,成为中国历史上一位杰出的数学家.这样出题,既活跃了课堂气氛,又达到了教学效果.

3.2 穿插相关的数学故事,借以发挥激励和榜样作用

在讲授数学知识时适当介绍数学家的思想方法;在讲授过程中应有意识地强调数学的德育价值.

如“历尽艰辛的负数”、“无理数的诞生与第一次数学危机”等,让学生明白这些符号或概念的产生是多么来之不易,从而萌发掌握好这些知识的思想.教师还可适当介绍一些现在已废弃不用但与现在能使用的数学符号具有联系的古代数学符号及理论表述形式,进行比较,有助于学生理解现在使用的这些符号和表述形式的优点,从而加深印象,更好地使用.

案例 (2)基本不等式——柯西和他的一个精彩的证明.

同学们,今天我们学习均值不等式：

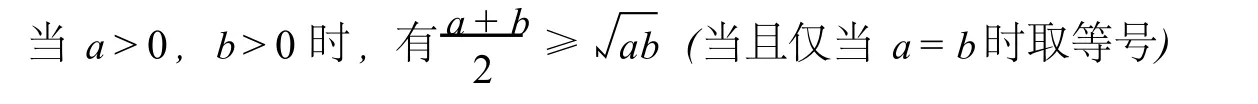
把它推广到n元:

当a1,a2,L,an＞0时,有(当且仅当 a1=a2=L=an时取等号)

18世纪法国著名数学家柯西 (Cauchy)给出了精彩的证明.柯西在代数学、几何学、误差理论以及天体力学、光学、弹性力学等方面都有出色的贡献.他发现和创立的定理和公式,往往是一些简单,最基本的事实.柯西是第一个用不等式来刻画极限过程的人;柯西建立了一个应用非常广泛的不等式——柯西不等式.

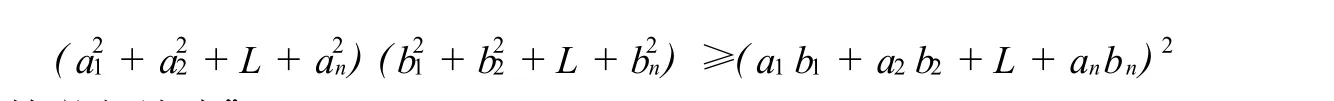
柯西还创立了“反向数学归纳法”.

柯西是怎样巧妙证明多元均值不等式?先看下面的一个不等式的证明思路:

设 a,b,c≥0,求证:a3+b3+c3≥3abc.

学生从这里得到了什么启发呢?留待课后思考讨论.

3.3 教师应恰当地向学生展示数学及发现过程、数学家的思维过程

如“勾股定理”的学习,有必要向学生介绍刘徽的“出入相补”原理的证明方法,展现他的证明过程.这样,学生就不单单只看到经过严格论证的结果,即成功的记录,而是看到数学家思维活动的过程,感受到了数学家敏锐的洞察力和机智,对培养学生数学思维具有启发意义.因为学生解题活动中的探索性思维与数学家从事研究活动的探索性思维本质上是相通的.从刘徽、赵爽等人都能通过不同途径达到证明“勾股定理”的目的中,学生还可得到启示,即一道数学的证明方法或解法有多种多样,在学习中不应满足于一种证法、一种解法,而应充分发挥自己的智慧,不断挖掘潜能,寻求最佳解题方法.

总之,数学史渗透到数学教育中,将数学认识为一种文化现象,对于教师来说是很重要的.有了这样的观念,教师的数学教学活动与人的个性发展联系起来就有了思想基础.中国数学基础教育有一个很大的优势,即注重基础知识和基本技能基础上进一步延伸到思想和方法、精神等文化的层次,那么中国数学教育的发展潜力将是巨大的.不过,教师在向学生介绍数学家故事时,目的应取其最能触动人心、最能净化学生心灵的部分来讲,而不是把“整桶水”都浇到学生头上,导致一节课下来,学生倒是听了不少有趣的故事,却没真正学到什么数学知识.

[1] 李正银.数学史与数学教育 [J].海南师范学院学报,2003,16(3)：98-101

[2] 周友士.数学史在数学新课程中的教学意义 [J].数学通报,2005,44(4)：17-19

[3] 孙铃.试论数学史对数学教育的意义 [J].辽宁教育行政学院学报,2005,22(4)：100