三维表面微观形貌建模与微通道流动特性仿真*

王清辉 郑旭 潘敏强 李静蓉

(华南理工大学机械与汽车工程学院∥表面功能结构先进制造广东普通高校重点实验室，广东广州510640)

随着材料科学与制造技术的发展，有别于传统机械加工的表面功能结构研究正逐渐成为许多科学与工程应用领域的热点问题.传统机械加工主要是以获得低的表面粗糙度、高的尺寸和形状精度为目标，而表面功能结构制造通常需要在材料表面制造出具有不同形貌、不同尺度和维数，且能够耦合一定的物理或化学功能的微细结构［1］.对表面功能结构的研究已成为机械工程学科的新增长点［2］.

由于表面功能结构的多样性与复杂性，对表面功能结构的多尺度形貌统一建模是进行其数字化设计的核心问题.然而，目前在设计领域普遍使用的建模技术主要是针对单一尺度下的宏观规则形体，难以直接应用于具有多尺度多维数特征的表面功能结构建模中.笔者所在实验室近年来的相关研究表明，对表面功能结构的建模可以包括两个主要部分，即宏观尺度(包括主结构和亚结构)的三维拓扑建模以及宏观表面的微观粗糙形貌表征建模［1］.其中，对微观形貌的有效描述对于揭示表面功能结构所耦合的物理化学功能具有重要意义［3］.尼古拉斯［4］在20世纪上半叶所做的关于粗糙表面对流动阻力特性影响的研究表明，只有在粗糙表面的相对粗糙度小于5%时，其对于层流特性的影响一般才可以忽略.张程宾、Kandlikar等［5-6］的相关研究发现，由于微尺度条件下表面粗糙形貌对流动和换热的影响，微通道内的流动和传热与常规尺度通道有很大不同.在微尺度条件下，虽然流动一般保持在层流状态，但研究发现其不同于常规尺度下的阻力特性，因此粗糙形貌对层流流动阻力的影响需要得到更为深刻的认识.为了研究粗糙形貌对微通道中流动特性的影响规律，需要有一种能精确描述粗糙度表面轮廓的几何方法.因而，在表面功能结构三维拓扑模型的基础上，客观、准确地表征其表面微观粗糙形貌是对表面功能结构设计和制造进行仿真的重要基础.

现有的粗糙形貌对层流流动特性影响的相关研究中已建立了随机波峰［7］、多孔介质模拟［8］、高斯分布［9］等描述表面粗糙度的模型，但这些模型都是建立在统计平均的基础上，无法准确表征表面微观形貌.为了有效描述自然界中广泛存在的不规则几何形貌，美国数学家Mandelbrot于1975年首次提出了分形几何学［10］.有研究表明机械加工表面具有统计意义上的自仿射分形特性［11］，这说明也可以像描述自然界的非规则结构一样，使用分形几何对机械表面微观形貌进行表征建模.张程宾等［5］将分形特征引入到矩形微通道的粗糙表面建模中，为简化计算，其假定表面粗糙形貌沿一个直线方向作分形变化，并基于该模型开展了微通道流动特性的仿真研究.

作为机械加工表面，表面功能结构的微观粗糙形貌也具有自仿射分形特性，在理论上分形几何可以为表面功能结构的微观粗糙形貌建模提供理论支持.但与普通机械加工表面不同的是，表面功能结构的粗糙形貌与表面微亚结构存在紧密的叠加效应，而且受具体加工工艺的影响，微观形貌在宏观上可能存在沿不同方向的分布异性等.文中针对表面功能结构的数字化设计需求，基于机械加工表面微观形貌中存在的自仿射分形特性，研究了将Weierstrass-Mandelbrot分形(简称W-M分形)与宏观的CAD实体模型相合成的数学方法，以支持金属表面功能结构的多尺度形貌建模.在此基础上，结合本实验室采用微犁削工艺在金属薄片上制造的V型微流体通道，以该微通道中的微流体特性为仿真研究对象，建立了多尺度形貌模型，并利用Fluent流体仿真软件进行数值模拟，同时分析了雷诺数、粗糙度和分形维数等对流动特性的影响，为进一步开展微通道表面功能结构的设计与制造提供理论与实验基础.

1 三维表面微观形貌的分形模拟

1.1 表面粗糙轮廓的分形表征

在机械工程领域，对机械加工表面的分形建模已成功应用于表面摩擦机理的相关研究［12］中.由于大多数机械加工表面粗糙形貌存在形态统计学上的自仿射特性，这意味着经局部放大后，其几何特征与放大前的整体轮廓非常相似(见图1).从纳米尺度到毫米尺度的表面粗糙度的轮廓可以由W-M函数(公式(1))进行表征［11］.根据分形几何学的观点，分形轮廓函数R(x)可以被认为是一个处处连续又处处不可导、且具有自仿射分形特征的曲线.

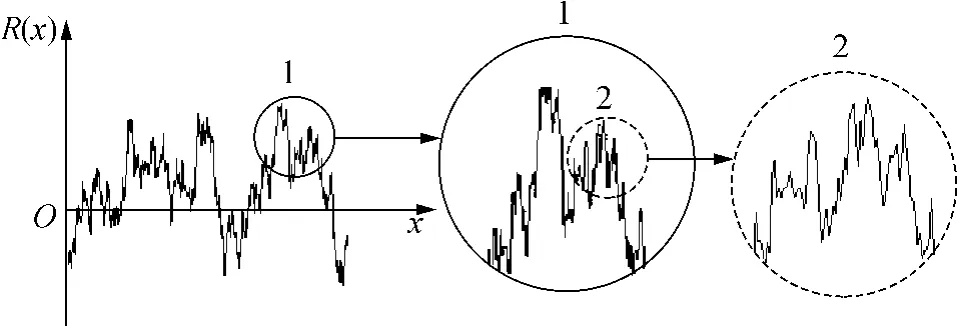
图1 表面轮廓统计学上的自相似性Fig.1 Statistical self-affinity for a surface profile

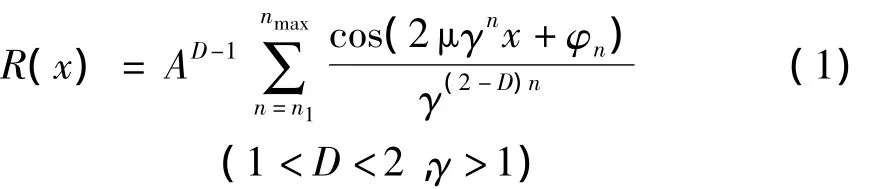
根据公式(1)构造出来的表面粗糙度的分形特征沿x轴方向变化.式中:A是尺度系数，D是取值范围在(1，2)的二维轮廓分形维数，A和D独立于扫描仪器的分辨率和测量尺度;n是频率指数;φn是随机相位，用来避免轮廓中的点位频率出现一致;γ是确定频谱密度和自身性质的尺度参数，取值通常为1.5.在W-M函数中，通常指定ωl=γn1为最低截止频率，ωh=γnmax为最高截止频率.nmax实际上是轮廓余弦函数形状的数量，在公式(1)中只有当nmax→∞时才是真正意义上的分形.在实际的仿真计算中，ωl由样本长度Ls决定，取值为ωl=1/Ls;ωh和扫描仪器的分辨率δ相关联，取值为ωh=1/(2δ).σ代表一个轮廓的均方根表面粗糙度，则尺度系数可以表示为

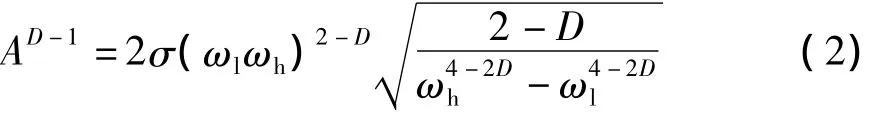
因此，一旦确定了参数D和σ，便可以建立一个基于W-M分形描述的、更为真实的表面粗糙轮廓的数学描述.

1.2 W-M分形与参数曲面相合成的数学描述

公式(1)是基于平面直线轮廓的分形描述，即分形形貌R(x)沿x轴发生，然而对于具有自由形状的曲线曲面零件，其表面粗糙形貌的发生独立于零件的宏观几何形状.如果直接将曲线的参数域值u替代x作为自变量，必然导致W-M函数轮廓发生一定程度的变形，因为相等的参数增量对应的弧长增量会因为曲线局部性质的不同而不均匀.例如，在曲线斜率较大的位置，W-M分形曲线被“拉长”，在斜率较小的位置被“压短”等，这不符合机械加工表面粗糙形貌分形特征的本质.因而，在本研究中假定其机械加工表面粗糙形貌是微观粗糙分形的轮廓高度变化与宏观参数曲面相合成的结果，而微观的分形轮廓不受参数曲线的自身几何性质影响.如图2及公式(3)所示，对于一条由参数u控制的自由参数曲线C(u)，其表面粗糙轮廓F(u)可表示为分形轮廓ΔR(u)沿局部法矢量N(u)与参数曲线C(u)的几何叠加;另外，对应于该分形轮廓的自变量应该采用的是曲线的自然参数，即累积弦长S(u).这样，可以将自由曲线上的分形轮廓理解为将线性W-M分形轮廓沿曲线轮廓自然卷曲后的几何结果，因而其分形特征独立于曲线轮廓的整体几何形貌.

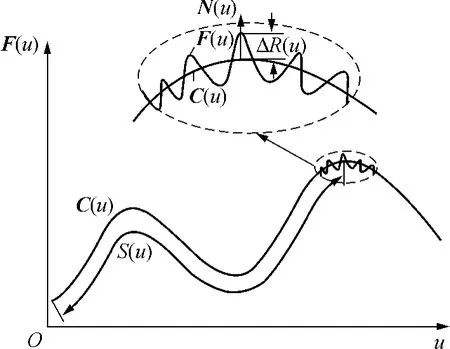
图2 粗糙分形轮廓与参数曲线的合成Fig.2 Synthesis of coarse fractal profile and parametric curves

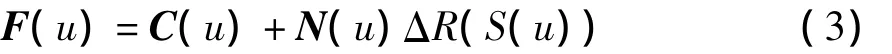
式中，

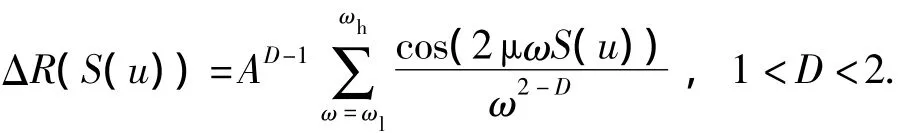
需要指出的是，对于大多数自由曲线，其累积弦长的计算难以通过解析计算直接获得.在算法实现上，文中采用弦长逼近的方法计算出累积弦长.如公式(4)所示，上述W-M分形与自由曲线S(u)合成的基本方法可以推广到三维空间的自由参数曲面S(u，w)模型:

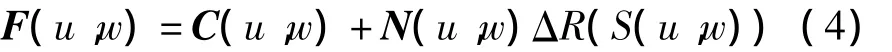
式中，

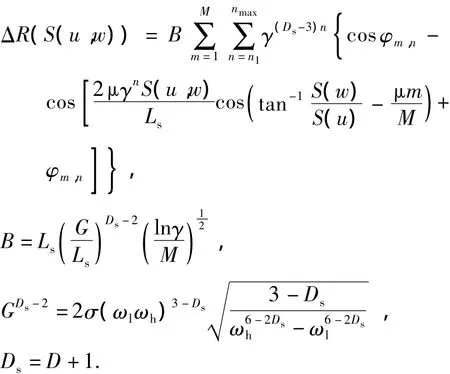
S(u，w)表示由u、w两个参数域控制的自由参数曲面，其具体数学描述形式可以是Bezier曲面，或是NURBS曲面等，而S(u)、S(w)则分别表示该曲面上参数位置(u，w)沿u、w两个方向上的累积弦长; φm，n则表示一个随机相位，其意义与公式(1)中的φn相同;γ与公式(1)中有相同的物理意义和量级; Ds(2＜Ds＜3)是三维表面形貌的分形维数;B是表面的高度系数;参数M是用于控制空间形貌起伏的参数;G是表面高度尺度系数，独立于频率，可以将仪器测量得到的均方根粗糙度σ代入前面公式中得到.

基于上述数学模型，文中利用AutoCAD平台提供的二次开发系统Object ARX，开发了用于表面功能结构粗糙形貌模拟的建模软件.它能够在宏观自由曲线曲面上合成W-M分形形貌，并可通过IGES、STL等数据接口导出，供第三方软件进行仿真计算.图3展示了在实体模型上通过分形参数控制而合成的不同表面粗糙形貌.

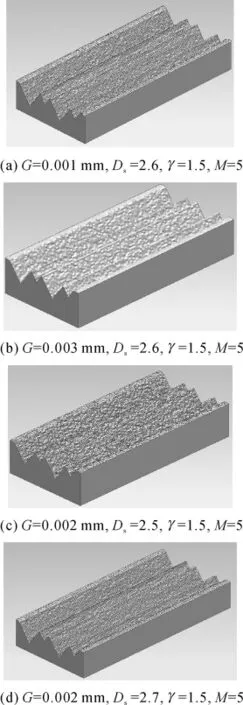
图3 在实体模型上合成的表面粗糙分形形貌的部分实例Fig.3 Examples of synthesis of coarse fractal topography and solid surfaces

2 微通道中的流动特性仿真

2.1 数字化模型的建立

在文献［5］研究工作的基础上，结合笔者所在实验室采用微犁削工艺在金属薄片上制造的V型微流体通道［1］，进一步采用公式(4)提出的合成算法，将W-M分形形貌与其宏观形貌相合成，构造了具有多尺度特征的V型微通道的三维数字化模型(见图4).基于该多尺度模型，文中分析了表面微观形貌与微通道中流动特性之间存在的耦合关系.

图4所示的微通道模型的槽深为0.24 mm，夹角为30°，长度为2 mm.为简化模型、减小后期计算量，需要作一些适当的假设以提高计算效率.假定微通道的侧面为根据W-M函数构建的三维分形特征的粗糙面，其余表面为光滑平面，并假设微流体在微通道内只发生层流流动.

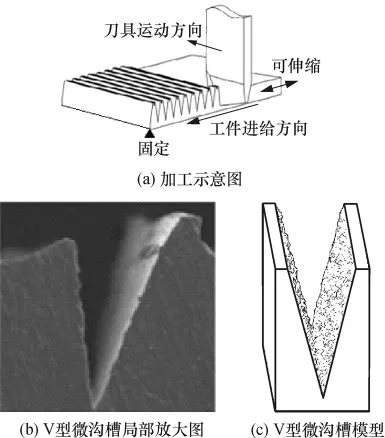
图4 V型微通道模型示意图Fig.4 Diagrammatic sketch of V-shaped microchannel

在建立微尺度层流流动模型时，作如下假设: (1)稳态层流;(2)常物性;(3)忽略重力影响.已有的研究表明［13］，Navier-Stokes方程对于微通道中的层流流动仍然有效.因此，运用有限元法进行仿真计算的可靠性得到了保证.

入口处给定流体速度vin边界条件，出口处达到流动充分发展，对于通道壁面，采用无滑移速度边界.

层流流动中的摩擦阻力系数［14］:

式中，L是微通道长度，Δp是通道进出口压差，ρ是流体密度，de是通道的水力直径.

2.2 求解思路与方法

模型的计算采用CFD软件中应用最广泛的Fluent流体仿真软件，流场采用分离求解法求解，压力与速度的耦合应用控制容积有限差分法和SIMPLE算法完成.网格由GAMBIT软件生成，应用四面体网格进行网格划分.在进、出口两端及粗糙壁面分布相对较密的网格节点，以使结果更为精确.当相邻两次迭代之间的流体速度残差小于10－6时，认为迭代计算收敛.

3 表面微观形貌对层流流动的影响

3.1 光滑微通道和粗糙微通道的沿程压力比较

图5给出了粗糙微通道和光滑微通道沿程压力(p)损失的比较.微通道模型的控制参数为:G= 0.002mm、Ds=2.6，仿真计算中设定的雷诺数Re= 900.从图5中可以看出:微通道内层流流动由于表面不再光滑，水流的流动受到了影响，这加剧了沿程压力的损失，因此粗糙微通道的沿程压力损失要大于光滑微通道;在入口段，粗糙微通道与光滑微通道的压力相差不大，但粗糙形貌对沿程压力损失的影响随距离的增加越发明显.

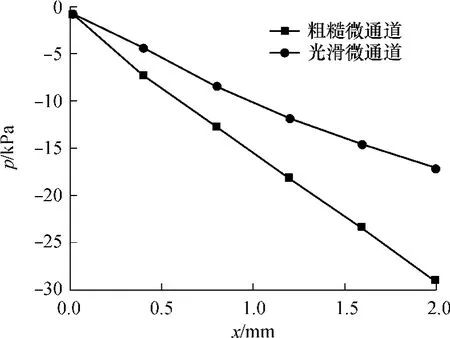
图5 微通道沿程压力Fig.5 Frictional pressure along with the microchannel

3.2 雷诺数对摩擦阻力系数的影响

图6给出了粗糙微通道(G=0.002 mm、Ds= 2.6)和光滑微通道的阻力系数f随雷诺数Re变化的曲线.由图6中可见:阻力系数随雷诺数的增大而减小，且阻力系数在雷诺数较小时变化较快;随雷诺数的增大，阻力系数的变化逐渐减缓.另外，光滑微通道的阻力系数明显要小于粗糙微通道的阻力系数，这是因为流体流经粗糙表面时受到了粗糙边界的扰动，导致压降增加.

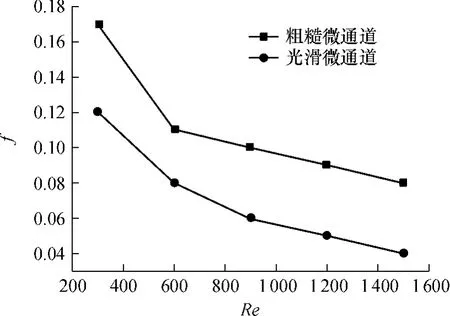
图6 雷诺数对摩擦阻力系数的影响Fig.6 Influence of Reynolds number on frictional resistance coefficient

3.3 表面高度尺度系数对摩擦阻力系数的影响

图7所示为粗糙微通道(Re=900，Ds=2.6)的阻力系数f随表面高度尺度系数G的变化.由图7中可见，阻力系数随通道表面高度尺度系数G的增大而增大.这是因为流体流过粗糙表面所产生的回流和分离现象导致了流体局部流动阻力的产生.随着表面高度尺度系数的增大，粗糙度也随之增大，粗糙表面周围流体的回流和分离对流动压降的影响也越来越显著.

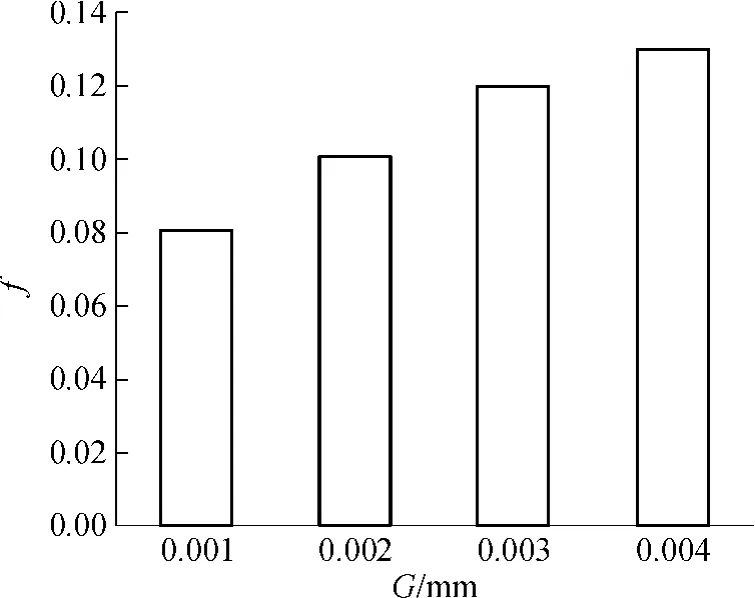
图7 表面高度尺度系数对摩擦阻力系数的影响Fig.7 Influence of surface height scale coefficient on frictional resistance coefficient

3.4 分形维数对摩擦阻力系数的影响

图8所示为粗糙微通道(Re=900、G=0.002mm)的阻力系数f随分形维数Ds的变化.

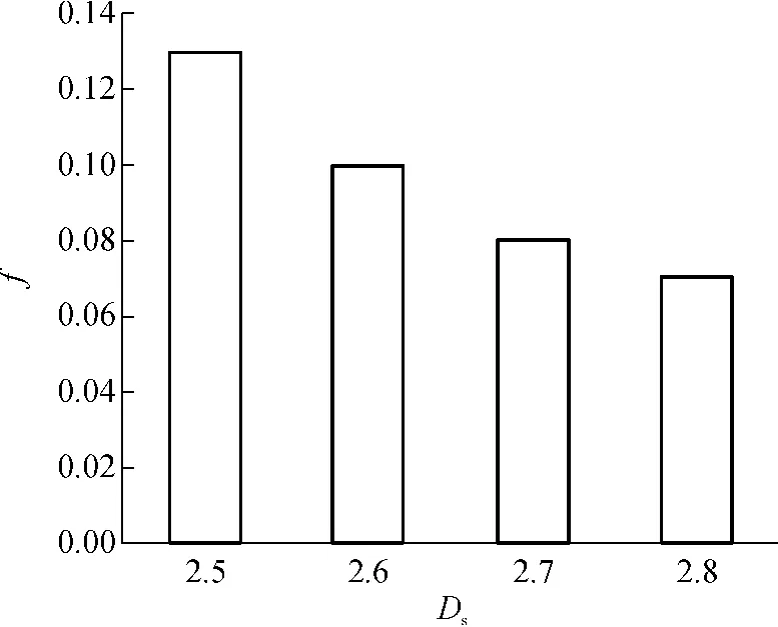
图8 分形维数对摩擦阻力系数的影响Fig.8 Influence of fractal dimension on frictional resistance coefficient

根据W-M函数仿真得到的表面形貌具有分形自相似性，在表面高度尺度系数G不变的情况下，随着分形维数Ds的增加，表面粗糙形貌趋于光滑;分形维数大的表面具有更复杂、更深层次的自相似性的精细结构，这类似于车削加工表面和磨削加工表面的区别.车削加工的表面，表面粗糙度大而分形维数小;磨削加工的表面，表面粗糙度小而分形维数大，表面结构更加精细［12］.因此，根据W-M函数，随着表面形貌分形维数的增加，通道阻力系数减小，这包括了粗糙度和分形维数的共同影响.在后续工作中，有必要研究在恒定粗糙度和雷诺数条件下分形维数对阻力系数的影响.

4 结语

文中探索了将W-M分形与三维参数曲面相合成的数学方法，该方法能够将表面功能结构的微观粗糙形貌与宏观CAD模型相集成，从而支持表面功能结构的多尺度形貌建模.通过改变表面高度尺度系数、分形维数等控制参数，可以构造出具有不同特征的粗糙形貌.基于上述建模方法，以微通道反应器的V型微通道中的微流体流动特性为仿真研究对象，建立了其多尺度形貌并存的仿真模型，在此基础上初步分析了雷诺数、表面高度尺度系数和分形维数等对流动特性的影响.该仿真研究对于多尺度微通道的设计与制造具有一定的指导意义，需要指出的是，针对多尺度微通道的流体流动特性仿真是一项复杂的工作，仍需进一步结合实验研究对文中所提出的仿真研究工作予以不断的细化与验证.

［1］ 汤勇，潘敏强，汤兴贤.表面热功能结构制造领域的发展及关键技术［J］.中国表面工程，2010，23(1):1-8.Tang Yong，Pan Min-qiang，Tang Xing-xian.Development and key manufacture technique of functional surface structures for heat transfer［J］.China Surface Engineering， 2010，23(1):1-8.

［2］ 雷源忠.我国机械工程研究进展与展望［J］.机械工程学报，2009，45(5):1-11.Lei Yuan-zhong.Recent research advances and expectation of mechanical engineering science in China［J］.Chinese Journal of Mechanical Engineering，2009，45(5): 1-11.

［3］ Senin N，Groppetti R.Surface microtopography design and manufacturing through topography descriptors:an application to prosthetic implant surfaces［J］.Computer Aided Design，2005，37(11):1163-1175.

［4］ 尼古拉斯.粗糙管中的水流的规律［M］.张瑞瑾，译.北京:水利出版社，1957:10-15.

［5］ 张程宾，陈永平，施明恒，等.表面粗糙度的分形特征及其对微通道内层流流动的影响［J］.物理学报，2009，58(10):7050-7056.Zhang Cheng-bin，Chen Yong-ping，Shi Ming-heng，et al.Fractal characteristics of surface roughness and its effect on laminar flow in microchannels［J］.Acta Physica Sinica，2009，58(10):7050-7056.

［6］ Kandlikar S G.Exploring roughness effect on laminar internal flow-are we ready for change［J］.Nanoscale and Microscale Thermophysical Engineering，2008，12(1): 61-82.

［7］ Croce C，Agaro P D.Numerical analysis of roughness effect on microtube heat transfer［J］.Superlattices and Microstructures，2004，35(3/4/5/6):601-616.

［8］ Kleinstreuer C，Koo J.Computational analysis of wall roughness effects for liquid flow in micro-conduits［J］.Journal of Fluids Engineering，2004，126(1):1-9.

［9］ Bahrami M，Yovanovich M M，Culham J R.Pressure drop of fully developed，laminar flow in rough microtubes［J］.Journal of Fluids Engineering，2006，128(3):632-637.

［10］ Mandelbrot B B.The fractal geometry of nature［M］.New York:Freeman，1983.

［11］ Majumdar A，Tien C L.Fractal characterization and simulation of rough surface［J］.Wear，1990，136(2):313-327.

［12］ 葛世荣，朱华.摩擦学的分形［M］.北京:机械工业出版社，2005:112-114.

［13］ Qu W L，Mala G M，Li D Q.Pressure-driven water flows in trapezoidal silicon microchannels［J］.International Journal of Heat and Mass Transfer，2000，43(3):353-364.

［14］ Harms T M，Kazmierczak M J，Gerner F M.Developing convective heat transfer in deep rectangular microhannels［J］.International Journal of Heat and Fluid Flow，1999，20(2):149-157.