基于主元分析和BP神经网络对刀具VB值预测

聂 鹏 谌 鑫

(沈阳航空航天大学 机电工程学院，沈阳 110136)

基于主元分析和BP神经网络对刀具VB值预测

聂 鹏 谌 鑫

(沈阳航空航天大学 机电工程学院，沈阳 110136)

对声发射信号进行5层小波分解提取6个频段的能量值，把它与切削速度、切削深度、进给量和切削时间一起作为刀具状态的特征向量.通过主元分析进行降维、消除特征向量间的相关性后，把得到的主元作为BP(Back Propagation)神经网络的输入向量.BP神经网络应用改进的LM(Levenberg-Marquart)算法进行学习，利用输入向量对网络进行训练后，实现对刀具后刀面磨损量VB的预测.实验结果显示:基于主元分析和LM算法改进的BP神经网络建立的预测系统，网络输出与实测VB值的误差0.03以内;根据预测VB值的范围可判别出刀具的不同状态.

主元分析;LM算法;BP神经网络;VB值预测

刀具状态直接影响工件的加工质量，为了保证加工精度，在不同的切削条件下，对刀具磨损状态进行判别具有重要的意义［1］.采集刀具的声发射信号，进行小波变换得到声发射信号能量值，作为反映刀具磨损状态的主特征［2］.由于切削的三要素和切削时间对刀具磨损有影响，把它们作为反映刀具磨损状态的辅助特征.把主特征和辅助特征一起构成的特征向量通过主元分析进行降维及消除矢量间的相关性之后，再作为BP(Back Propagation)神经网络的输入向量.输入向量的维数即为主元的个数.本文采用LM(Levenberg-Marquart)算法改进的BP神经网络［3］，该网络结构为3×7×1，实现对后刀面磨损量VB值的预测.基于主元分析和LM算法改进的BP神经网络具有收敛快，误差小的优点，能够较准确地预测出VB值，进而对刀具状态进行判断.

1 提取声发射信号的能量

声发射与刀具切削状态相关程度高，具有灵敏度高，响应快的特点，非常适合作为反映刀具状态的特征［4］.本文将刀具状态分为3种:VB值小于0.2mm 为正常切削;VB 值介于0.2～0.3mm之间为一般磨损;VB值大于0.3mm为严重磨损.使用硬质合金刀具车削高温合金材料，在主轴转速为 280 r/min、进给量为 0.2mm/r、切削深度为0.3mm的切削参数下采集3种不同状态的声发射信号，对信号用db10小波进行五层分解，并作出频带-能量图，刀具在3种状态下能量变化明显，如图1所示.在6种不同的切削条件下分别采集刀具3种状态下的声发射信号共18组，并提取每组信号的6个频带的能量值与切削三要素及实际VB值，如表1所示.

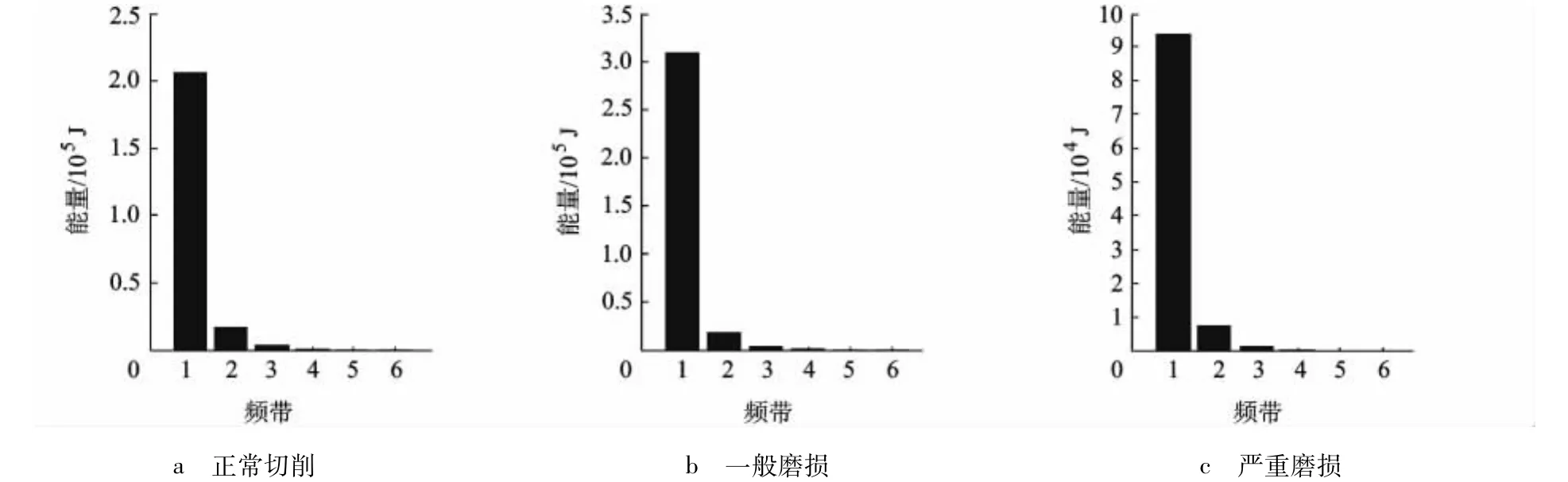
图1 刀具不同状态下的能量图

2 主元分析

主元分析是一种特征提取方法，其核心思想就是通过将相关的一组数据集进行降维，并尽量保留原来数据集的变化信息.其目的是在数据空间中找出一组m个正交矢量，它们最大可能地表示数据方差，以便将数据从原始的n维空间映射到这组正交矢量所组成的m维子向量上，从而完成降维任务，得到主特征矢量［5］.

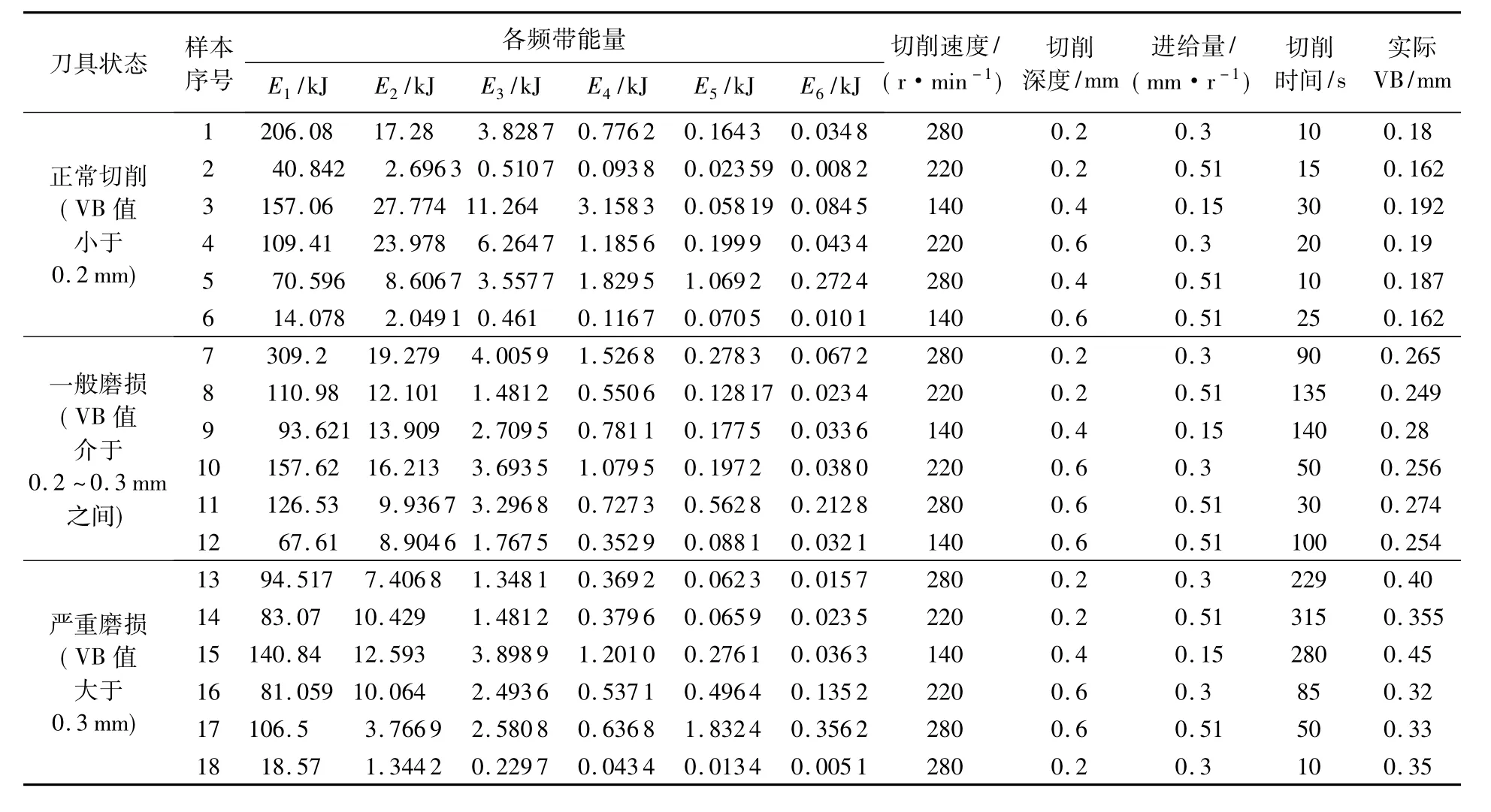
表1 刀具不同状态的声发射信号用db10小波分解后各频带的能量值、切削条件及实际VB值

设一个有n个样本点和m个变量的样本集合矩阵为 X∈Rn×m，协方差矩阵为 Σ∈Rm×m.设线性组合:T=XP，其中，T=(t1，t2，…，tm)(T∈Rn×m，ti∈Rn×1，i=1，2，…，m)为原始变量在主超平面上投影的综合变量;P=(p1，p2，…，pm)(P∈Rn×m，pi∈Rn×1，i=1，2，…，m)为变换矩阵.

如果满足下列条件:①ti与tj(i≠j)不相关;②ti=X pi的系数满足③t1是X满足条件②的一切线性组合中方差达到最大者，t2是与t1不同的一切X的线性组合中方差达到最大的，ti是与 t1，t2…，ti－1都不相关的一切 X 的线性组合中方差达到最大的，则称t1，t2，…，tm分别为X的第1主元，第2主元，…，第m主元［6］.

首先求取第1主元，设t1为第1主元，t1是变量 x1，x2，…，xm的线性组合:

要求得t1能携带最多的原始数据信息，即要求t1的方差取到最大值，t1的方差为

定义目标函数为

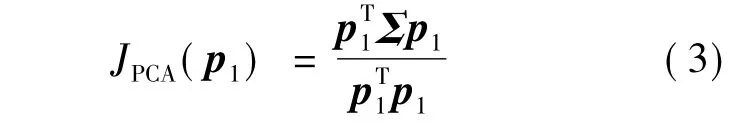
利用拉格朗日算法求解，定义拉格朗日函数为

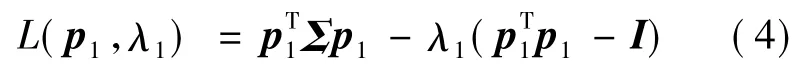
其中，λ1是拉格朗日算子.对L求p1的偏导，并令其为0，有

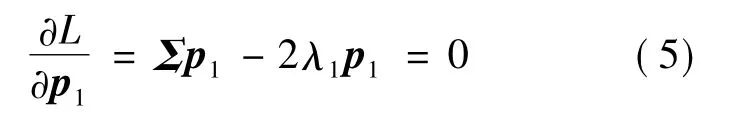
由上式可得

由此可知，p1是协方差矩阵Σ的一个特征向量，λ1是它对应的特征.由式(2)和式(6)可得

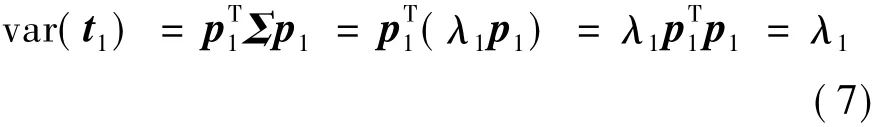
因此，欲使t1的方差达到最大值，即要求的p1是协方差矩阵Σ的最大特征值λ1所对应的特征向量.这里p1称为第1主轴，第1主元t1即可由式(1)求得.

依此类推，可求得X的第i主元ti和第i主轴pi.pi是协方差矩阵Σ的第i个次大特征值λi所对应的特征向量.则第i主元ti为

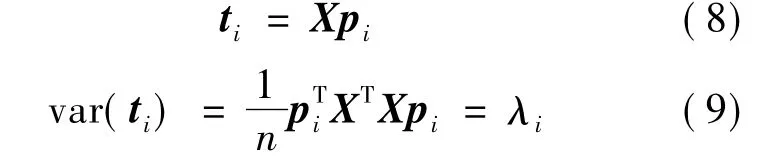
由此有，var(t1)≥var(t2)≥…≥var(tm).因此，用数据变异大小来反映数据中的信息，则第1主元t1携带的信息量最大，t2次之，依此类推.

把表1中各频带能量、切削速度、切削深度、进给量和切削时间的数据先进行标准化处理，再经过主元分析后得到表2，由表2可知，原始数据从10维降到了3维，大大减小了数据的处理量.把降维后得到的3个主元作为反映刀具状态的特征向量输入BP神经网络.

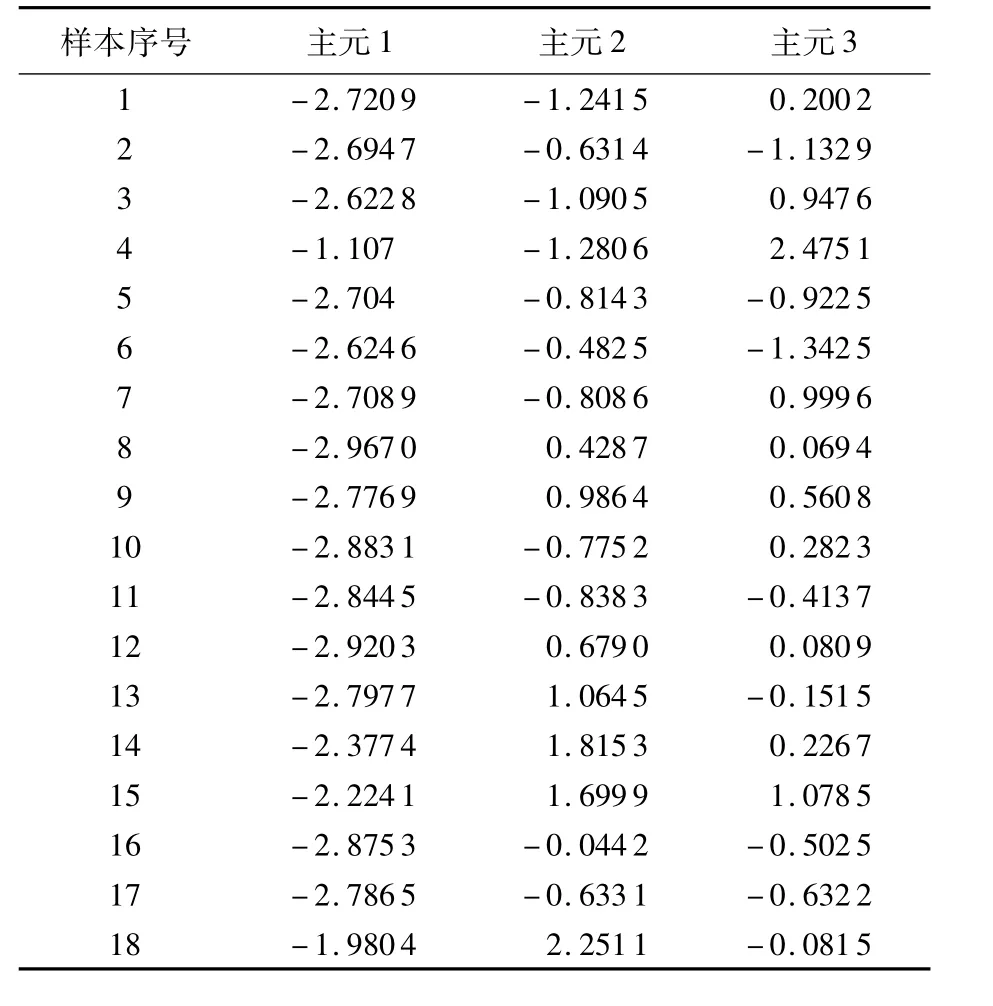
表2 经主元分析的方法对表1的原始数据进行降维

3 LM算法的BP神经网络

3.1 BP神经网络结构

BP网络结构属于多层网络，分为输入层、中间层和输出层，层与层之间多采用全连接方式，同一层单元之间不存在互连.BP神经网络通常具有一个或多个隐层，其中隐层神经元通常为sigmoid型传递函数，而输出层神经元则采用purelin型传递函数［7］.如果需要对网络的输出进行限制，在输出层要采用s型函数，输出就在一个很小的范围内(如在0～1之间);若采用线性激活函数，则可以使网络输出任何值.

在模式样本相对较少的情况下，本文选择两层BP神经网络，采用LM学习算法.由表2可知特征向量(主元)个数为3，即网络输入节点数为3;设神经网络的输出为VB值，则输出层节点数为1;隐层节点数的确定是通过同一样本集训练，当网络输出误差最小时得到的，本例选择7;所以网络结构为3×7×1.

3.2 LM学习算法

LM算法实际上是梯度下降法和牛顿法的结合，是为了在以近似二阶训练速率进行修正时避免计算Hessian矩阵而设计的［8］.梯度下降法在开始几步下降较快，但随着接近最优值时，由于梯度趋于0，使得目标函数下降缓慢;而牛顿法可以在最优值附近产生一个理想的搜索方向.LM法的搜索方向定为

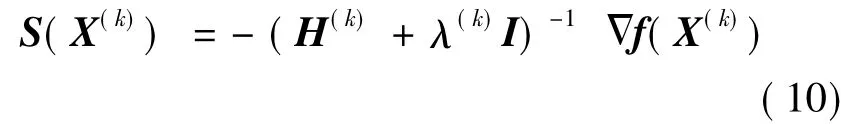
其中，H(k)为Hessian矩阵;λ(k)为由网络的所有权值和偏差值组成的向量;f(X(k))为目标函数;Δf(X(k))表示目标函数的梯度.

当λ=0时，式(10)即为牛顿法;当λ的值很大时，式(10)变为步长较小的梯度法.牛顿法逼近最小误差的速度最快，更精确，因此应尽可能使算法接近于牛顿法，在每一步成功地迭代后(性能误差减小)，使λ值减小;仅在进行尝试性迭代后的性能误差增加的情况下，才使λ增加.这样，该算法每一步迭代的误差性能总是减小的.

4 实验分析

把表2中序号为1～4，7～10，13～16作为训练样本对BP神经网络进行训练;序号为5～6，11～12，17～18作为对应序号为1～6的测试样本对已训练好的BP网络进行VB值预测.图2为BP神经网络的误差性能曲线，由图可知该网络经过12次训练后收敛，收敛速度快，误差小.图3所示的是网络输出与实测VB值的误差曲线，由曲线可知，该误差在0.03以内，有较好的精度.经过主元分析的测试样本的网络输出VB值见表3.

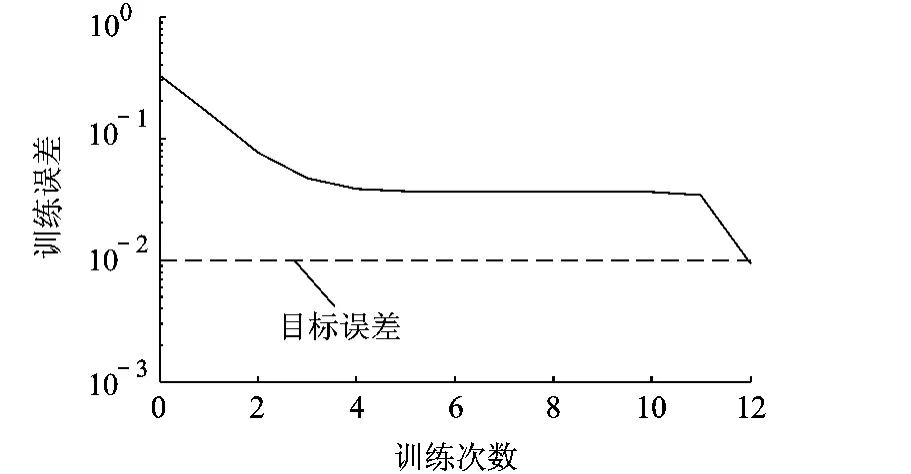
图2 用主元分析后的训练样本BP网络误差性能曲线

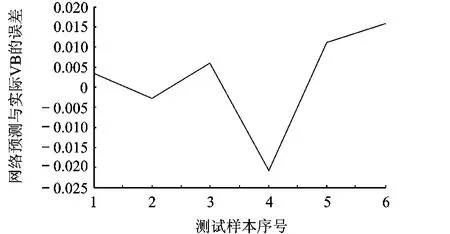
图3 用主元分析的测试样本(VB值)误差曲线

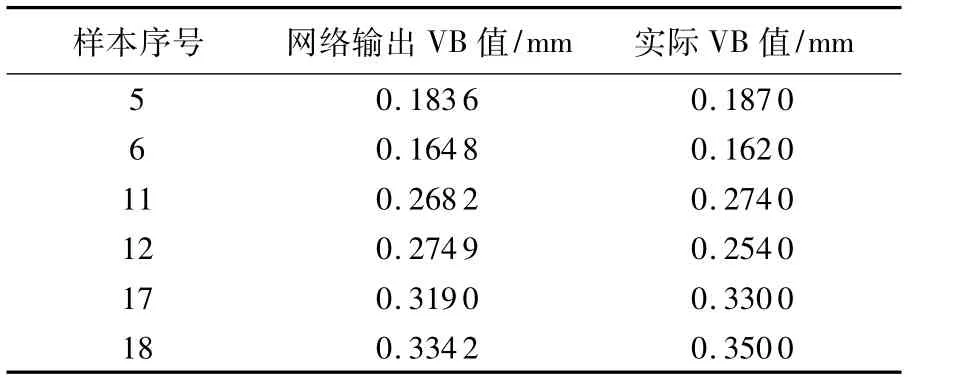
表3 用主元分析的测试样本网络输出值

把表1中没有用主元分析的能量值、切削三要素及切削时间一起作为BP神经网络的输入向量，序号为1～4，7～10，13～16作为训练样本;序号为5～6，11～12，17～18作为测试样本.BP神经网络误差性能曲线和测试样本的预测值与实测值的误差曲线分别如图4、图5所示.

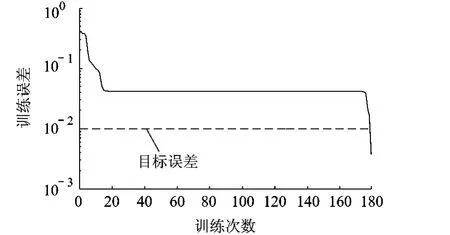
图4 没经过主元分析的训练样本BP网络误差性能曲线

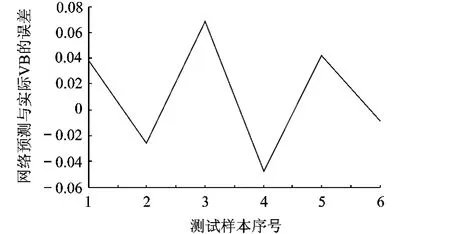
图5 没经过主元分析的测试样本(VB值)误差曲线

由图4、图5可知，BP网络经过179次训练才收敛，且测试样本输出的VB值最大误差为0.08.没经过主元分析的测试样本网络输出值如表4所示.

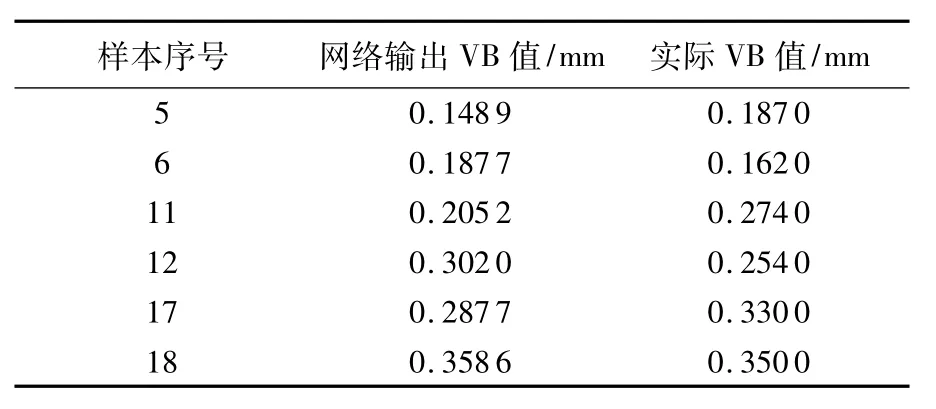
表4 没经过主元分析的测试样本网络输出值

5 结论

特征向量经过主元分析后，减小了数据的维数，进而输入神经网络后大大提高了运算速度.由实验结果对比可知，经过主元分析的训练样本，BP神经网络经过12次训练就收敛，且测试样本输出的VB值最大误差为0.03，而没有经过主元分析的训练样本，BP网络经过179次训练才收敛，且测试样本输出的VB值最大误差为0.08.在基于主元分析和改进LM算法的BP神经网络对刀具VB值预测的系统中，能够根据输入刀具状态有关的特征向量，较准确地预测出VB值，且误差在0.03以内.

References)

［1］康晶，冯长建，胡红英.刀具磨损监测及破损模式的识别［J］.振动、测试与诊断，2009，29(1):5 －9 Kang Jing，Feng Changjian，Hu Hongying.Tool wear monitoring and pattern recognition of tool failure［J］.Journal of Vibration，Measurement＆ Diagnosis，2009，29(1):5 －9(in Chinese)

［2］ Tamura M，Tsujita S.A study on the number of principal components and sensitivity of fault detection using PCA［J］.Computers and Chemical Engineering，2007，31(9):1035 －1046

［3］ Balazinski M，Czogala E，Jemielniak K，et al.Tool condition monitoring using artificial intelligence methods［J］.Engineering Applications of Artificial Intelligence ，2002，15:73 －80

［4］郑金兴，张铭钧，孟庆鑫.多传感器数据融合技术在刀具状态监测中的应用［J］.传感器与微系统，2007，26(4):90 －93 Zheng Jinxing，Zhang Mingjun，Meng Qingxin.Application of multi-sensor data fusion in tool wearmonitoring［J］.Transducer and Microsystem Technologies，2007，26(4):90 － 93(in Chinese)

［5］ Li R Y，Rong G.Fault isolation by partial dynamic principal component analysis in dynamic process［J］.Chinese Journal of Chemical Engineering，2006，14(4):486 －493

［6］朱松青，史金飞.状态监测与故障诊断中的主元分析法［J］.机床与液压，2007，35(1):241 －243 Zhu Songqing，Shi Jinfei.PCA approach to condition monitoring and fault diagnosis［J］.Machine Tool ＆ Hydraulics，2007，35(1):241－243(in Chinese)

［7］ Ghosh N，Ravi Y B，Patra A，et al.Estimation of tool wear during CNCmilling using neural network-based sensor fusion［J］.Mechanical Systems and Signal Processing，2007，21(1):466 －479

［8］张德丰.MATLAB神经网络仿真与应用［M］.北京:电子工业出版社，2009:168－174 Zhang Defeng.MATLAB neural network simulator and application［M］.Beijing:Electronics Industry Press，2009:168 －174(in Chinese)

(编 辑:李 晶)

Prediction of tool VB value based on PCA and BP neural network

Nie Peng Chen Xin

(School of Mechanical Engineering，Shenyang University of Aeronautics and Aviation，Shenyang 110136，China)

Five layers ofwavelet decomposition was applied on acoustic emission signals for extracting the acoustic emission(AE)signals energy value of six bands.Energy value and cutting speed，cutting depth，feed rate，cutting time were turned into state feature vectors of tool wear.The principal component analysis was used to reduce dimension and eliminate the correlation between the feature vectors.The principal components were seen as back propagation(BP)neural network input vector.Improved Levenberg-Marquart(LM)algorithm was used to BP neural network for learning，input vectors were trained for BP neural network.Then，the BP neural network would realize the forecast of tool flank wear VB value.The results indicate that the VB value forecast system based on principal component analysis(PCA)and the improved BP neural network with LM algorithm can accurately predict the tool flank wear VB value within the error range 0.03.The different states of tool wear can be judged according to the VB value.

principal component analysis(PCA);Levenberg-Marquart(LM)algorithm;back propagation(BP)neural network;forecast VB value

TP 183

A

1001-5965(2011)03-0364-04

2010-04-20

沈阳市人才引进专项基金资助项目(07SYRC04)

聂 鹏(1972－)，男，吉林省吉林人，副教授，niehit@163.com.