利于翼型优化设计的超临界翼型参数化方法
邓金秋 冯仁忠
(北京航空航天大学 数学与系统科学学院,北京 100191)
利于翼型优化设计的超临界翼型参数化方法
邓金秋 冯仁忠
(北京航空航天大学 数学与系统科学学院,北京 100191)
为减少超临界翼型优化中的设计变量,消除优化结果的不光顺现象、保证C2连续,在优化过程中控制翼型几何特性的变化范围,设计出了由4条首尾相接的有理Bézier曲线表示的超临界翼型的翼型参数化方法,该方法对翼型数据的参数化过程中主要运用了Bézier曲线拟合算法与SPSA(Simultaneous Perturbation Stochastic Approximation)优化算法,并在Bézier曲线拟合算法中使用了有别于常用方法的数据点参数选择方法.将这种超临界翼型参数化方法与优化算法结合便可实现翼型优化设计,其中的设计变量为21个,优化结果不仅光顺且满足C2条件,通过设定设计变量变化范围便可控制相应的翼型前缘半径、上下弦最高最低点的位置与曲率、尾部契角等几何特征.
翼型;曲线;参数化;优化
超临界翼型具有一些优良的气动特性,在民航客机和大型运输机的设计中有着广泛的应用.基于气动性能数值计算的超临界翼型优化设计具有周期短、费用低的优点.因此将数值模拟计算与风洞试验相结合可以缩短研发周期、降低研发费用,这已成为目前超临界翼型研究的发展方向[1-4].
为实现基于数值计算的超临界翼型优化,就需要设计相应的翼型参数化方法,即将由离散数据点表示的待优化翼型转化为由含参数的翼型函数表示,再选择翼型函数的适当参数作为设计变量,结合优化算法与流场计算实现优化设计.可见翼型参数化对于翼型优化设计来说是十分重要的[5-7].
现有的翼型参数化方法主要存在如下问题:①设计变量过多,如通过在基准翼型上添加局部扰动函数的方法会有多达数十个设计变量;②优化结果存在不光顺现象,如B样条表示方法[8]与Hicks-Henne外形函数法[9];③翼型函数不满足C2条件,如 Figures样条法[10];④很难在优化过程中约束翼型的特定几何特性的变化范围[11].为解决上述4点问题,本文结合超临界翼型的几何特性提出了一种基于分段有理Bézier曲线的超临界翼型参数化方法.通过这种方法得到的翼型函数共有21个参数,满足C2条件,不存在不光顺现象,并且翼型参数直接和翼型几何特征相对应.本文首先介绍翼型参数化的具体过程,然后结合SPSA(Simultaneous Perturbation Stochastic Approximation)优化算法给出具体的优化实例.
1 参数化方法
由于超临界翼型具有较复杂的几何形状,很难通过一条低次Bézier曲线表示,因此需要使用分段Bézier曲线表示翼型.另一方面为了降低翼型参数的个数,应尽量减少分段数目与每段Bézier曲线的次数.综合这两方面因素,本文提出了如下翼型参数化方法.
设翼型函数为C(t),C(t)由4条3次有理Bézier曲线C0(t)~C3(t)首尾相连拼接而成,曲线Ci(t)的4个控制顶点为,见图1.
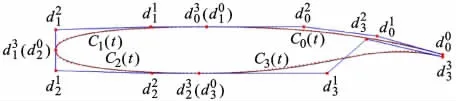
图1 翼型函数C(t)的组成形式
下面以 NASA SC(2)0712[12]为例介绍翼型参数化的具体步骤.
1.1 对控制顶点坐标的初步约束
首先将控制顶点权重均置为1,并对曲线控制顶点做如下初步设定:
C0(t)段曲线:将坐标值设为翼型后缘上表面最后一个数据点的坐标值;将坐标值设为翼型上弧线最高点坐标值,由于数据点足够密,可以直接设为数据点中纵坐标最大点坐标;将纵坐标值设为纵坐标值,使得与共线且水平;不对横坐标值与横纵坐标值进行任何设定.
C1(t)段曲线:将坐标值设为坐标值,使得与重合;将纵坐标值设为纵坐标值,使得和共线且水平;将坐标值设为翼型前缘顶端坐标值,由于数据点足够密,可以直接设为数据点中横坐标最小点坐标值;将横坐标值设为横坐标值,使得与共线且竖直;不对纵坐标值与横坐标值进行任何设定.
C2(t)段曲线:将坐标值设为坐标值,使得与重合;将横坐标值设为横坐标值,使得和共线且竖直;将坐标值设为翼型下弧线最低点坐标值,由于数据点足够密,可以直接设为数据点中纵坐标最小点坐标;将纵坐标值设为纵坐标值,使得与共线且水平,不对纵坐标值与横坐标值进行任何设定.
C3(t)段曲线:将坐标值设为坐标值,使得与重合;将纵坐标值设为纵坐标值,使得和共线且水平;将坐标值设为翼型后缘下表面最后一个数据点的坐标值;不对横坐标值与横纵坐标值进行任何设定.
通过初步设定,可以确定一部分控制顶点的坐标,这些坐标在之后参数化过程中均保持不变.而对于另一部分仍处于自由状态的控制顶点坐标则需要在下一个步骤中确定.
1.2 确定控制顶点坐标
通过对控制顶点坐标的初步约束可以发现,4条Bézier曲线的端点坐标均已确定了下来,因此每条曲线也自然对应了一段翼型数据点.下面就要确定仍处于自由状态的控制顶点坐标,使每段曲线最大限度贴合到其对应的一组数据点组.由于改变任意一条曲线不会对其它3条曲线产生影响,因此可以将4段Bézier曲线分别拟合到对应的数据点组上,进而求出所有的控制顶点坐标,下面以C1(t)为例说明拟合方法.对应的数据点组如下:
设C1(t)对应的数据点组为,用(xpj,ypj)表示 pj的坐标值,即设1],为Bernstein基函数,为C1(t)控制顶点,用表示的坐标值,即
由累积弦长法[13]得到对应参数,并将等比例变换到区间[0,1],使.下面使用最小二乘法确定使得最小.
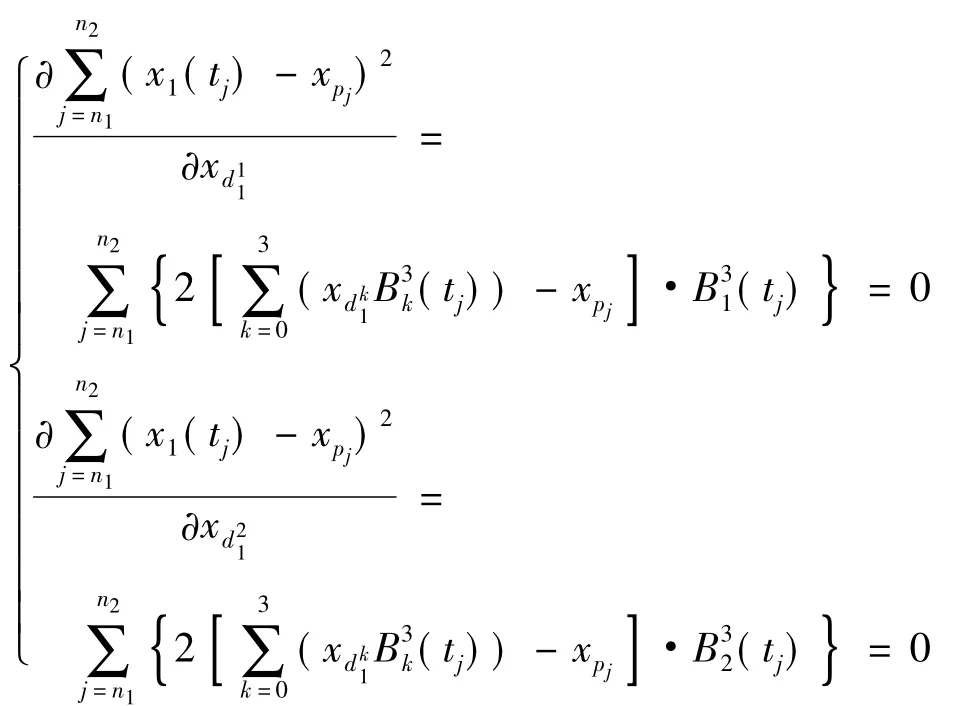

图2 初步计算结果

图3 由累积弦长法得到的对应关系

图4 数据点与曲线上与其横坐标相等点的对应关系

图5 以为参数进行最小二乘得到的结果

表1 误差降低速度
至此已完全确定了控制顶点坐标,在之后的参数化过程中所有控制顶点坐标均保持不变.
1.3 调整控制顶点权重使曲线满足C2条件
通过之前计算得到的翼型函数在Bézier曲线拼接点处仅满足C1条件,其他部分满足C2条件.拼接点曲率见表2.

表2 拼接点曲率
3 次有理 Bézier曲线有如下性质[13]:
1) 设4 个控制顶点权重为 w0,w1,w2,w3,那么可以在不改变曲线外形的前提下将4个控制顶点权重调整为 1,v1,v2,1,其中 v1,v2相互独立且由 w0,w1,w2,w3唯一确定.
2)保持控制顶点位置不变,设4个控制顶点权重为1,v1,v2,1 则 v1,v2与两个端点的曲率一一对应.
由上述两条性质可知3次有理Bézier曲线可以由4个控制顶点坐标和两个端点曲率唯一确定.为使拼接点处的曲率连续,只需固定控制顶点坐标,将相邻Bézier曲线在拼接点处曲率设为相同值.
显然人为给定拼接点处曲率,如设为相邻Bézier曲线在拼接点曲率的平均值,会导致之前得到的翼型函数出现较大变化,增大翼型函数与数据点之间的误差.所以不妨使用优化算法,以翼型函数与数据点的误差为优化目标,以3个拼接点的曲率为设计变量,使用 SPSA[14-15]方法进行优化计算.SPSA方法的主要思想是通过随机扰动各个设计变量使目标函数逐渐收敛到极小值,其算法如下:
Input:
SPSA 参数 a,c,A,α,γ;
/* 分别设为1,0.1,80,0.6,0.7*/
目标函数 y(θ0,θ1,θ2);
/*y(θ0,θ1,θ2)为翼型函数与数据点的误差,在保持控制顶点坐标不变的前提下仅与3个拼接点的曲率有关*/
Output:
Rθ0,Rθ1,Rθ2.
/*使得误差最小的3个拼接点曲率*/
Function:
for(k=0;;k++)
{
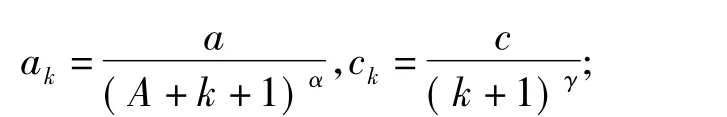
Δk=[Δk0,Δk1,Δk2]T;
//Bernoulli01(1,-1)
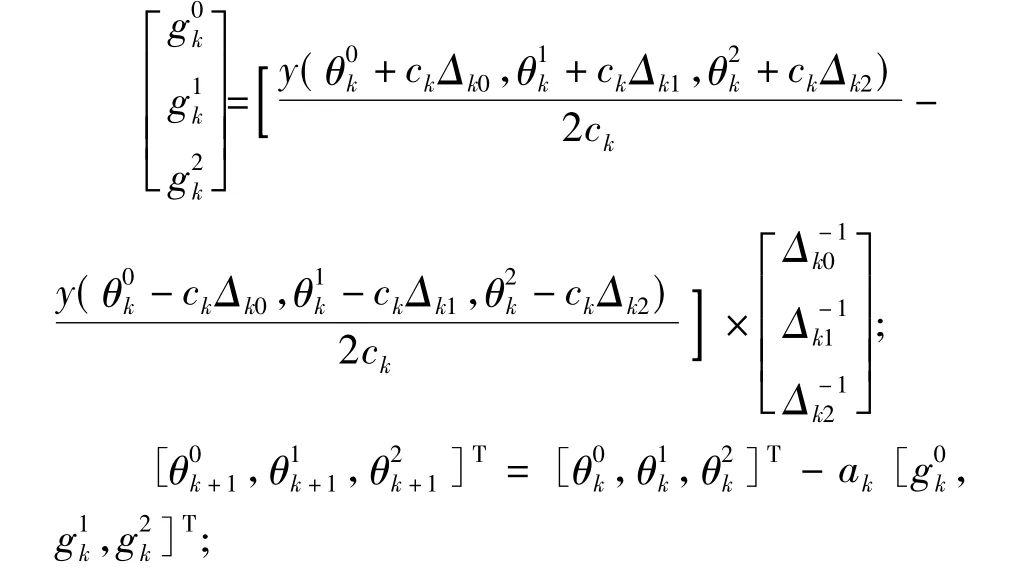

计算后误差为0.002 06,最终得到的翼型函数见图6.

图6 最终得到的翼型函数
将这种参数化方法应用于NASA SC(2)翼型库,翼型函数与数据点误差见表3.
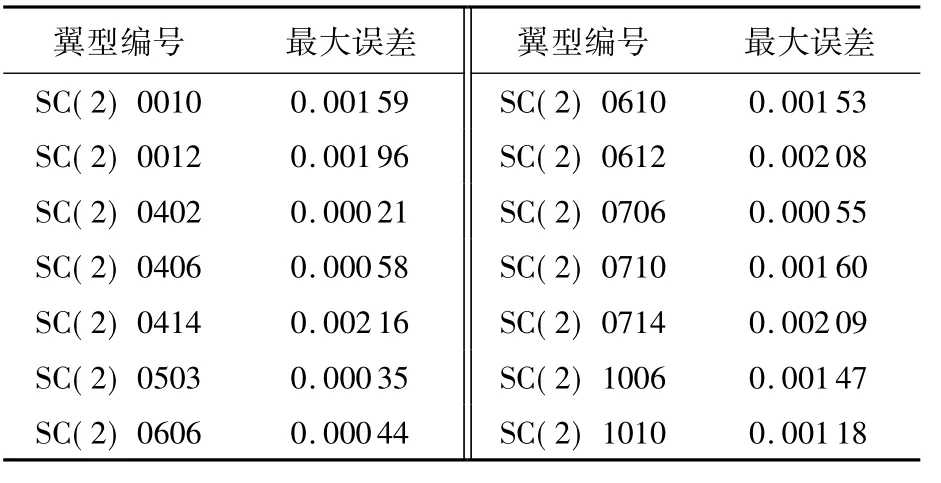
表3 翼型函数与数据点误差
表3表明这种翼型参数化方法可以较精确地表示常见的超临界翼型,因此可以为优化提供足够丰富的翼型搜索空间.
1.4 翼型参数的选择
翼型参数应满足如下两条性质:①通过翼型参数可以还原翼型函数;②各参数之间应相互独立.由于3次有理Bézier曲线可以由4个控制顶点坐标和两个端点曲率唯一确定,所以应选择4条有理Bézier曲线的控制顶点和端点曲率组成翼型参数{Pn}.但由于拼接点连续且曲率相等,上下两条控制边水平,前缘控制边竖直导致了{Pn}中含有相关联参数.
因此去除相关联参数,最终得到21个相互独立的参数:参数1(纵坐标)、参数2(横坐标)、参数3(纵坐标)、参数4(横坐标)、参数5(纵坐标)、参数 6(横坐标)、参数7(横坐标)、参数8(纵坐标)、参数9(纵坐标)、参数10(横坐标)、参数11(纵坐标)、参数 12横坐标)、参数13(横坐标)、参数14(横坐标)、参数15(纵坐标)、参数16(纵坐标)、参数17(处曲率)、参数18(处曲率)、参数 19(处曲率)、参数20(处曲率)、参数21(处曲率).
1.5 与其它参数化方法的比较
目前常用的翼型参数化方法为Hick-Henne外型函数法,该方法通过大量局部扰动函数的叠加来组合出翼型曲线.由于任意一段翼型曲线均为多个局部扰动函数叠加的结果,因此极易出现凹凸不平等不光顺现象.而通过本方法得到的翼型曲线是由3次有理Bézier曲线拼接而成,由于每段Bézier曲线的内部均是光顺的且拼接处满足C2条件,因此得到的翼型曲线具有很好的光滑度.与Hick-Henne外型函数法相比,本方法得到的翼型曲线不会出现不光顺现象,因此更有利于流场计算.
另一种经典的翼型参数化方法为Figures样条法.这种方法同样应用分段Bézier曲线表示翼型,但在两段曲线的拼接点只满足C1条件而不满足C2条件,因此所得翼型函数的曲率不连续.这就导致在流场计算的过程中会出现湍流现象,影响结果的准确性.而本方法保证了拼接点的C2连续性,进而确保了流场计算的准确性.
此外,现有的绝大部分翼型参数化方法都无法将翼型参数与翼型几何性质紧密的联系在一起,这就导致了翼型优化的盲目性.本方法所选取的翼型参数与翼型几何特性紧密相关,因此大大增强了翼型优化的目的性与针对性.
为说明将该翼型参数化方法应用与翼型优化设计的可行性,本文给出了具体的优化实例.
2 优化实例
由于本文讨论的重点在于构造翼型参数化方法,所以没有涉及流场计算与高效优化算法的设计.这里通过使用SPSA优化算法将基准翼型优化为目标翼型的方法来证明本文提出的翼型参数化方法可以应用于翼型优化设计.优化结果见表4、图7和图8.

表4 优化效果
图7所示优化算例中的基准翼型为SC(2)0503,目标翼型为SC(2)0706.图7a中离散点为目标翼型数据点,曲线为基准翼型,图7b中离散点为目标翼型数据点,曲线为优化结果.优化结果与目标翼型误差为0.001450.
图8所示优化算例中的基准翼型为SC(2)0614,目标翼型为SC(2)1010.图8a中离散点为目标翼型数据点,曲线为基准翼型,图8b中离散点为目标翼型数据点,曲线为优化结果.优化结果与目标翼型误差为0.001218.
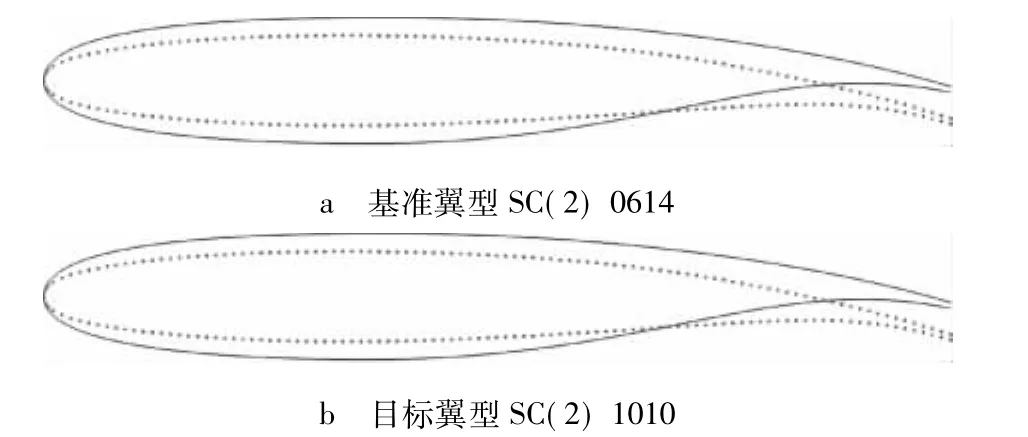
图8 将基准翼型SC(2)0614优化为目标翼型SC(2)1010
3 结论
本文给出的翼型参数化方法所含设计变量较少,共21个;设计的基于有理Bézier曲线的翼型函数不仅光顺且满足C2条件;参数与翼型几何性质对应,通过限制参数变化范围便可控制对应的几何参数;该方法可以为翼型优化提供足够丰富的翼型搜索空间.这些特性表明,该翼型参数化方法会为下一步的翼型优化提供很大的便利.此外分段有理 Bézier曲线可以很方便地转化为NURBS曲线,便于工程应用.
References)
[1]刘周,朱自强,付鸿雁,等.高升阻比翼型的设计[J].空气动力学学报,2004,22(4):410 -414 Liu Zhou,Zhu Ziqiang,Fu Hongyan,et al.Design of airfoil with high ratio of lift over drag[J].Acta Aerodynamica Sinica,2004,22(4):410-414(in Chinese)
[2]王晓璐,朱自强,刘周.基于N-S方程的翼型双设计点双目标优化设计[J].北京航空航天大学学报,2006,32(5):503-507 Wang Xiaolu,Zhu Ziqiang,Liu Zhou.Bi-point/bi-objective optimization design of ailfoil using N-Sequations[J].Journal of Beijing University of Aeronautics and Astronautics,2006,32(5):503-507(in Chinese)
[3]周涛,张淼,李亚林.基于全速势方程的超临界翼型设计[J].航空计算技术,2009,39(4):58 -64 Zhou Tao,Zhang Miao,Li Yalin.Supercritical airfoil design based on full potential equations[J].Aeronautical Computer Technique,2009,39(4):58 -64(in Chinese)
[4] Khurana M,Winar to H.Application of swarm approach and artificial neural networks for airfoil shape optimization[R].AIAA-2008-5954,2008
[5] Heine B,Mack S.Aerodynamic scaling of general aviation airfoil for low Reynolds number application[R].AIAA-2008-4410,2008
[6] Padulo M,Maginot J.Airfoil design under uncertainty with robust geometric parameterization[R].AIAA-2009-2270,2009
[7] Haderlie J,Crossley W.A parametric approach to supercritical airfoil design optimization[R].AIAA-2009-6950,2009
[8] Lepine J,Guibault F,Trepanier JY,et al.Optimized nonuniform rational B-spline geometrical representation for aerodynamic design of wings[J].AIAA,2001,39(11):570 - 577
[9] Hicks R M,Hennet P A.Wing design by numerical optimization[J].Journal of Aircraft,1978,15(7):407 -412
[10] Sobester A,Keane A J.Airfoil design via Cubic splines fer guson's curves revisited[R].AIAA 2007-2881,2007
[11] Song Wenbin,Keane A J.A study of shape parameterization methods for airfoil optimization[R].AIAA 2003-4482,2004
[12] Harris C D.NASA supercritical airfoils a matrix of family-related airfoils[R].NASA Technical Paper 2969,1990
[13] Farin G E.Curves and surfaces for computer-aided geometric design[M].4.San Diego:Academic Press,1997:53 - 56,172-224
[14] Spall JC.Implementation of the simultaneous perturbation algorithm for stochastic optimization[J].IEEE Transactions on Aerospace and Electronic Systems,1998,34(3):817 -823
[15] Song Qing,Spall JC,Ni Jie.Robust neural network tracking controller using simultaneous perturbation stochastic approximation[J].Neural Networks IEEE Transactions,2008,19(5):817-835
(编 辑:赵海容)
Supercritical airfoil parameterization method feasible to optimum design
Deng Jinqiu Feng Renzhong
(School of Mathematics and Systems Science,Beijing University of Aeronautics and Astronautics,Beijing 100191,China)
To reduce the number of design variables in the supercritical airfoil optimization,eliminate the unfairness phenomenon,ensure C2condition,control the geometric characteristics of the airfoil in the optimization process,a parameterization method for supercritical airfoil based on four rational Bézier curve was presented.In the parametric process to the airfoil data,the Bézier curve approximation algorithm and SPSA(simultaneous perturbation stochastic approximation)algorithm were used and in the Bézier curve approximation algorithm the way to choose the parameter to the data points is different from the common method.Supercritical airfoil shape optimization can be achieved by combining this method with optimization algorithms.It contents 21 design variables,the optimization result is fair and satisfies the C2condition,the geometric characteristics of the airfoil such as leading edge radius,upper and lower crest location including curvature there,the boat tail angle can be controlled in the optimization process by setting the range of the design variables.
airfoils;curves;parameterization;optimization
V 211.3
A
1001-5965(2011)03-0368-06
2010-01-25
邓金秋(1988 -),男,北京人,硕士生,deng.jinqiu@gmail.com.

