非完整链式系统的全局连续 K指数镇定

李明军 马保离

(北京航空航天大学 自动化科学与电气工程学院,北京 100191)

非完整链式系统的全局连续 K指数镇定

李明军 马保离

(北京航空航天大学 自动化科学与电气工程学院,北京 100191)

为非完整链式系统提出了两种全局连续反馈控制律,即连续时变反馈控制律和动态时不变反馈控制律.第 1种控制律通过引入一个与状态初值有关的指数衰减项,来保证控制律的连续性和渐近性.第 2种控制律通过引入一个可自由设定初值的辅助状态,来保证系统的可控性以及控制律的连续性和渐近性.这两种控制律可以保证系统所有状态以指数速度渐近地、连续地收敛到原点,克服了以往控制律不能同时具有连续性、渐近性和指数收敛速度的缺陷.所得控制律应用于移动机器人系统和一个 4维链式系统的镇定,仿真结果表明:状态轨迹和控制轨迹的光滑度和收敛速度都要优于以往控制律.

非完整链式系统;全局 K指数镇定;连续时变控制;动态反馈控制;移动机器人

非完整链式系统的控制是近年来非线性控制领域的热点问题,其原因有两点:①很多带速度约束的实际机械系统可以通过变换局部地或全局地转换成非完整链式系统[1];②非完整链式系统不满足文献[2]中的必要条件,无法用静态连续状态反馈对其进行渐近稳定.

为此,人们先后设计出不少控制方案.一种是时变反馈控制律.文献[3]首次提出光滑时变反馈控制方法,并将其用于链式系统.文献[4]证明了无漂可控系统能够通过光滑时变反馈达到渐近稳定,文献[5-6]对多输入链式系统使用了时变反馈控制,但是文献[4-6]的收敛速度仅为多项式.文献[7]为链式系统提出的不连续时变控制律获得了全局 K指数稳定性,但它依赖于预定义时间点集和高频振荡函数.为获得具有指数收敛速度的光滑时变控制律,文献[8-9]分别为移动机器人运动学模型和链式系统引入指数衰减项,文献[10-11]分别为链式系统和高阶链式系统引入辅助状态.文献[12]为链式系统提出动态级联反馈线性化方法,获得了渐近稳定性,但未讨论收敛速度.文献[13]获得了链式系统的全局一致渐近稳定性,但未达到指数收敛速度.

另一种方法是不连续时不变控制方法.文献[14]将 σ-过程运用于链式系统,首次获得了全局K指数稳定,但控制律不连续.文献[15-16]将σ-过程运用于不确定性链式系统,获得了全局渐近稳定性,但是没有达到指数收敛速度.文献[17]提出了一种不连续非正则反馈变换用于链式系统,获得了指数收敛速度,但不是渐近稳定的.

在文献[9-10]的基础上,本文提出了两种全局连续时变控制律,同时获得了连续性、渐近稳定性和指数收敛速度.

1 概念和引理

则称系统为全局 K指数稳定的.

与指数调节不同,K指数稳定具有优良特性:“初始状态离原点越近,整个轨迹也离原点越近”[14].

引理 1 如果 n阶矩阵 A的所有特征值的实部小于 -a(a＞0),则系统是全局K指数稳定的,其中 ξ∈Rn,‖α(t)‖ ≤α0(‖ξ(0)‖ )e-bt,α0(· )是 K类函数,a＞b＞0.

证明 易知 Lyapunov方程:

有唯一正定对称解阵 P.定义 Lyapunov函数 V=ξTPξ,则有 μ1‖ ξ‖2≤V≤μ2‖ ξ‖2,其中 μ1和 μ2分别是 P的最小、最大特征值.·V满足:

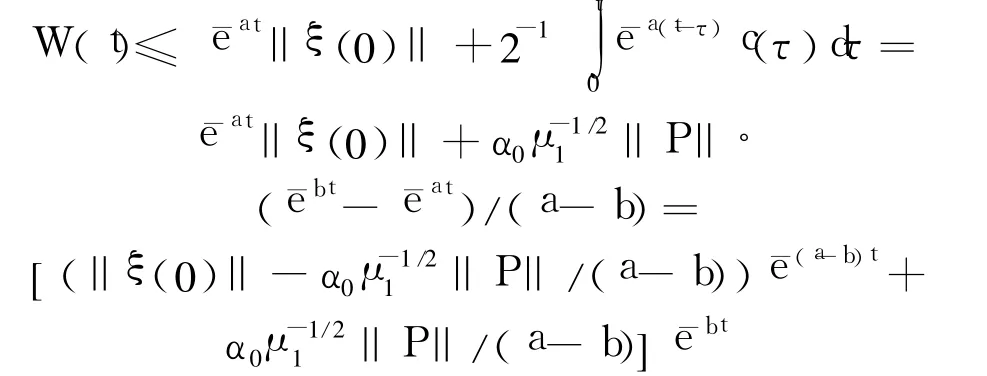
证明 易知 Lyapunov方程:

有唯一正定对称解阵 P.定义 Lyapunov函数 V=ξTPξ,则有 μ1‖ ξ‖2≤V≤μ2‖ ξ‖2,其中 μ1和 μ2分别是 P的最小、最大特征值.V的时间导数为

2 连续时变状态反馈

考虑非完整单链系统:

其中,n＞2;X=[x1,…,xn]T为状态;u1和 u2为控制输入.式(1)的全局连续时变 K指数镇定问题可以叙述为:设计连续控制律 u1(X,t)和u2(X,t),使得式(1)是全局 K指数稳定的.

引理 3 对于式(1),控制律:

使得状态 x1(t)指数收敛到原点,其中 α(t)=α0(‖X(0)‖)e-λ1t;k1＞λ1＞0;α0(· )是某个 K类函数.

对于闭环子系统 x·1=-k1x1+α(t),由线性系统理论可知,当 X(0)≠0时,有

定义向量:

当 X(0)≠0时,引入如下坐标变换和控制输入:

其中,T(α)=diag(1,1/α,…,1/αn-2)为变换阵;K=[k2,…,kn]T为反馈系数.对式(5)两边进行微分,并利用式(1)和式(3),可得到如下闭环系统:

其中

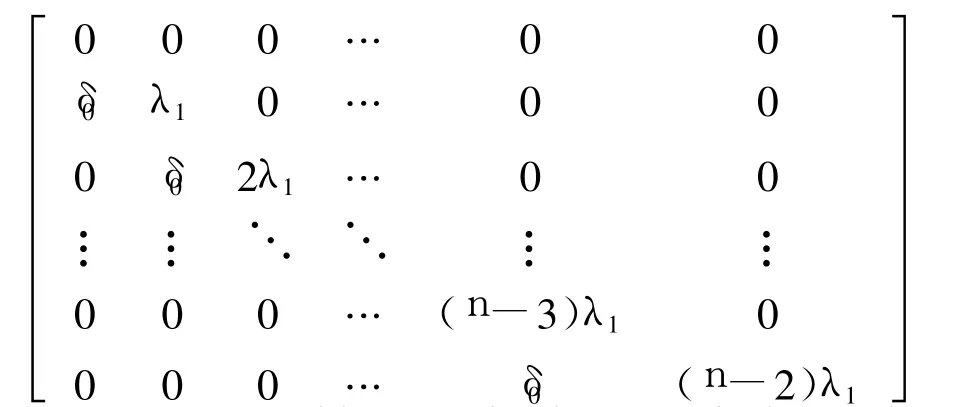
定理 1 选择 k1＞λ1＞0,选择 K使得 A1-B1K的所有特征值的实部小于 -k(k＞0),并令,则在式(2)和式(8)

作用下,式(1)是全局 K指数稳定的.

证明

1)显然,u1是连续的.易知:

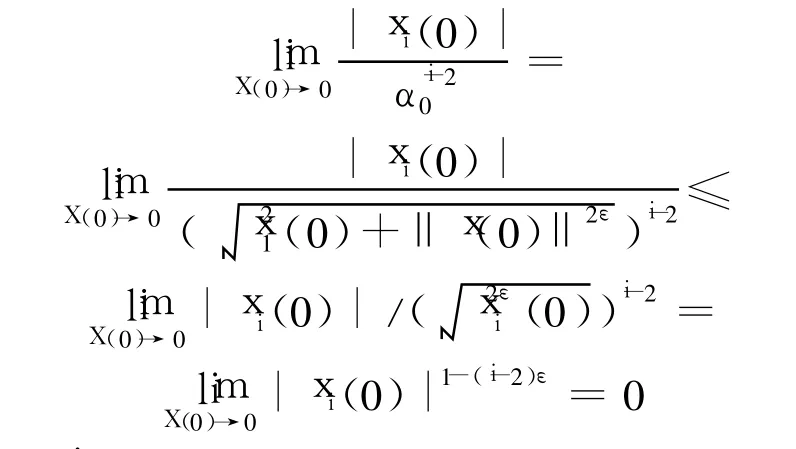
其中,i=3,4,…,n,于是

因此 u2是连续的.

2)由式 (2)和式(8)可知,当 X(0)=0时,有u1(t)≡u2(t)≡0.结合式(1),可知 X(t)≡0.

由式(5)可知:

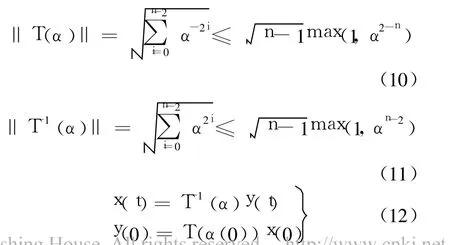
将式(9)～式(11)代入式(12),可得

由 α0的定义式可知是的 K类函数,且

定义函数:

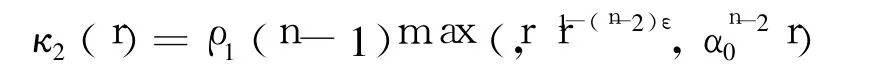
因 0＜ε＜1/(n-2),故 κ2(· )是 K类函数.将κ2(· )和式 (14)代入式(13),即有

由引理 3和式(15)可知,式(1)的整个轨迹满足:

其中,κ3(·)=κ1(·)+κ2(·)是 K类函数.

证毕

3 动态时不变状态反馈

文献[10]为式(1)添加辅助状态 x0,使得x·0=x1,并设计控制律 u1=-k1x1-k0x0使得子系统(x0,x1)指数收敛到原点.然后提取慢变模态e-bt(b＞0),用该模态施加光滑可逆的 σ-过程,得到带指数衰减项的线性扰动系统,再设计光滑时变控制律 u2,使得其他状态(x2,…,xn)指数收敛到原点.与文献[9]类似,文献[10]没有获得 K指数稳定性.改进措施就是用状态 x0和 x1的某个组合对其他状态施加 σ-过程,使得状态渐近地指数收敛到原点.这种改进的代价就是控制律 u2将仅仅是连续的,而不是光滑的.

式(1)的全局动态时不变状态反馈 K指数镇定问题可叙述为:设计连续动态反馈控制律u1(X,x0)和 u2(X,x0),使得式(1)是全局 K指数稳定的.

引理 4 引入动态状态反馈:

其中,x0为辅助状态;,则闭环轨迹(x0(t),x1(t))和控制输入 u1(t)将指数收敛到原点.

证明 将式(16)代入式(1),可得闭环系统:

设该系统的特征值被配置为 -λ1,-λ2(0＜λ1＜λ2).式(17)是引理 1的特例,故有

显然,(x0(t),x1(t))和 u1(t)是指数收敛的.证毕

选取状态(x0(t),x1(t))的如下组合:

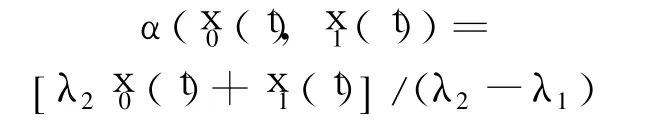
根据式(17)的解的关系可得

式中

式中

与第 2节的控制方案类似,根据式(4)定义向量 x和 y,当 X(0)≠0时,根据式(5)和式(6)引入 y=T(α)x和 u2=-Ky,则由式 (1)和式(20)可得闭环系统:

其中,A2,B2和 L2的形式与上文定义的 A1,B1和L1完全一样,但是 A2中的 δ0和 L2(t)中的 δ1(t)由式(21)定义.

定理 2 按照引理 4选择 k1和 k0,选择 K使得 A2-B2K的所有特征值的实部小于 -k(k＞(n-2)λ1),并按照下式辅助状态的初值:

其中,0＜ε＜1/(n-2),则在式(16)和式(24)

作用下,式(1)是全局 K指数稳定的.

证明

1)同定理 1的 1).

2)由式(16)和式(24)可知,当 X(0)=0时,有 u1(t)≡u2(t)≡0,因此有 X(t)≡0.

3)将式(23)代入式(18),可得

4)假设 X(0)≠0.由式(23)可知:

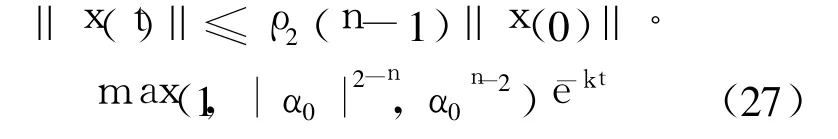
由式(19)和式(23)可知

故‖x(0)‖ |α0|n-2的上界是‖X(0)‖的 K类函数κ5(r)

利用式(23),可得

定义函数:

因 0＜ε＜1/(n-2),故 κ6(· )是 K类函数.将κ6(· )和式 (28)代入式(27),可得

由式(25)和式(29)可知,系统的整个轨迹满足:

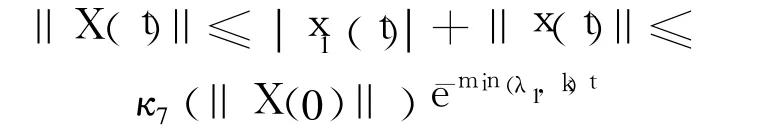
其中,κ7(·)=κ4(·)+κ6(·)是 K类函数.

证毕

4 仿 真

4.1 连续时变状态反馈

使用文献[9]的控制律和初始状态(x,y,θ)=(1,-1,π/4)和(1,-1,π/4)/100,仿真结果如图 1所示.由图 1可见,当初始状态各分量绝对值缩为1/100时,角度 θ的振幅几乎没变.这说明文献[9]的控制律的局部特性不佳,即当初始状态非常靠近原点的时候,角度 θ仍然需要大幅度的改变之后才能回归原点.

图 1 文献[9]的仿真结果

针对两个初始状态(1,-1,π/4)和(1,-1,π/4)/100,使用本文的控制律,结果如图 2所示.由图 2可见,当初始状态各分量绝对值缩为1/100时,各分量的振幅随之缩为 1/10左右.这说明本文控制律的局部特性优于文献[9],即初始状态越靠近原点,只需要越少的调整,就能镇定到原点.

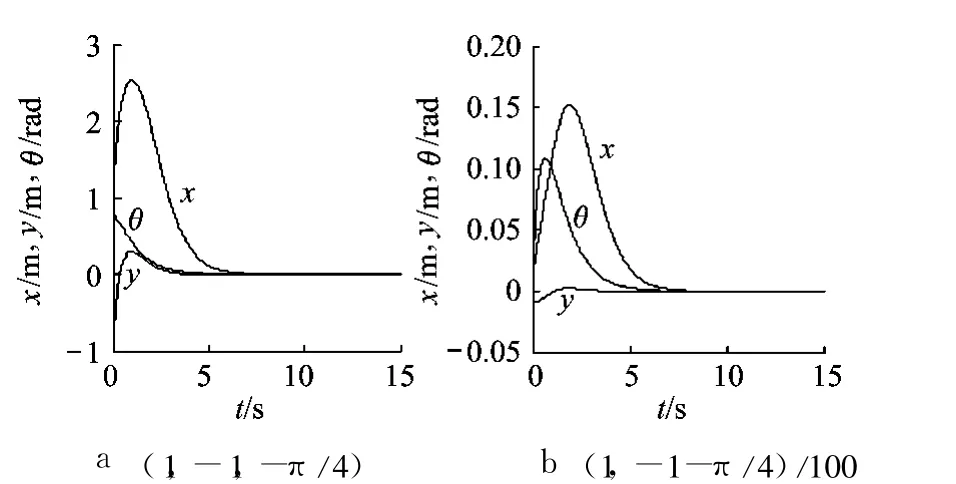
图 2 本文第1个控制方案的仿真结果

4.2 动态时不变状态反馈

文献[10]针对 4维链式系统进行了仿真,初始状态为(x1,x2,x3,x4)=(0,-1,0.5,0.5),辅助状态 x0的初值为 x0=2,仿真结果如图 3a所示.然后将初始状态改为(0,-1,0.5,0.5)/100,但初值 x0=2不变,仿真结果如图 3b所示.由图 3可见,当初始状态各分量绝对值缩为 1/100时,分量 x1的振幅几乎没变.这说明文献[10]的控制律的局部特性不佳,即当初始状态非常靠近原点的时候,x1仍然需要大幅度的改变之后才能回归原点.

针对两个初始状态(0,-1,0.5,0.5)和(0,-1,0.5,0.5)/100,使用本文的控制律,仿真结果如图 4所示.由图 4可见,当初始状态各分量绝对值缩为 1/100时,各分量的振幅随之缩为 1/3左右.这说明本文控制律的局部特性优于文献[10],即初始状态越是靠近原点,只需要越少的调整,就能镇定到原点.

图 3 文献[10]的仿真结果

图 4 本文第2个控制方案的仿真结果

5 结束语

针对非完整链式系统,提出了两种同时具有连续性、渐近性和指数收敛速度的反馈控制律,使得闭环系统被全局镇定,改善了前人的研究成果.

References)

[1]Kolmanovsky I,McClamroch N H.Developments in nonholonom ic control problems[J].IEEE Control Systems Magazine,1995,15(6):20-36

[2]Brockett RW,Millman R S,Sussmann H J.Differential geometric control theory[M].Boston:Birkhauser,1983:181-191

[3]Samson C.Velocity and torque feedback control of a nonholonomic cart[C]//Advanced RobotControl Proc Int Workshop Nonlinear Adaptive Control:Issues in Robotics.Grenoble:Springer,1991:125-151

[4]Coron J M.Global asymptotic stabilization for controllable systems without drift[J].Math Contr Sig Syst,1992,5:295-312

[5]Jiang Z P.Iterative design of time-varying stabilizers for multi-input systems in chained form[J].Systems＆Control Letters,1996,28(5):255-262

[6]Walsh GC,Bushnell L G.Stabilization of multiple in put chained form control systems[J].Systems＆Control Letters,1995,25(3):227-234

[7]Sordalen O J,Egel and O.Exponential stabilization of nonholonomic chained systems[J].IEEE Translation on Automatic Control,1995,40(1):35-39

[8]Li Chuanfeng,Wang Chaoli.Robust stabilization of kinematic systems of uncertain nonholonomicmobile robots[C]//Proceedings of the 6th World Congress on Intelligent Control and Automation.Piscataway,N J:IEEE,2006:1142-1146

[9]Ma B L,HuoWei.Smooth time-varying exponential stabilization of nonholonomic chained systems[J].Acta Automatica Sinica,2003,29(2):301-305

[10]Tian Yuping,Li Shihua.Global smooth time-varying exponential stabilization of nonholonomic chained systems[C]//Proceedings of the 3rd World Congress Intelligent Control and Automation.Hefei,China:University of Science and Technology of China Press,2000:3328-3342

[11]Tian Yuping,Li Shihua.Exponential stabilization of nonholonomic dynamic systems by smooth time-varying control[J].Automatica,2002,38(7):1139-1146

[12]Wang Jing,Qu Zhihua,Hull A Richard,et al.Cascaded feedback linearization and its application to stabilization of nonholonomic systems[J].Systems＆Control Letters,2007,56(4):285-295

[13]Lee T C,Jiang Z P.On uniform global asymptotic stability of nonlinear discrete-time systems with applications[J].IEEE Transactions on Automatic Control,2006,51(10):1644-1660

[14]March and N,Alamir M.Discontinuous exponential stabilization of chained form systems[J].Automatica,2003,39(2):343-348

[15]Ju Guiling,Wu Yuqiang,SunWeihai.Adaptive output feedback asymptotic stabilization of nonholonomic systems with uncertainties[J].Nonlinear Analysis,2009,71(11):5106-5117

[16]Zheng Xiuyun,Wu Yuqiang.Adaptive output feedback stabilization for nonholonomic systems with strong nonlinear drifts[J].Nonlinear Analysis,2009,70(2):904-920

[17]Sun Zhengdong,Ge S S,Huo Wei,et al.Stabilization of nonholonomic chained systemsvianonregular feedback linearization[J].Systems＆Control Letters,2001,44(4):279-289

(编 辑:赵海容)

Global K-exponential stabilization of nonholonomic chained system s by continuous feedback

Li Mingjun Ma Baoli

(School of Automation Science and Electrical Engineering,Beijing University of Aeronautics and Astronautics,Beijing 100191,China)

Two global continuous feedback control laws were proposed to stabilize nonholonomic chained systems,namely,the continuous time-varying feedback control law and the dynamic time-invariant feedback control law.The first control law achieved continuity and asymptotic ality by using an exponential decay term related to the initial state values,while the second achieved controllability,continuity and asymptotic ality by setting the initial value of the introduced assistant state variable.The two control laws could guarantee that all the states converged to zero continuously and asymptotically at exponential rates,which overcame the shortcomings that the previous control laws could notachieve continuity,asymptotic ality and exponential rates at the same time.The proposed control laws are app lied to the mobile robot and a four-dimension chained system.The simulation results show that the smoothness and convergence rates of the state/control trajectories are better than the previous works.

nonholonomic chained systems;global K-exponential stabilization;continuous time-varying control;dynamic feedback control;mobile robots

TP 13

A

1001-5965(2011)04-0452-06

2010-05-11

国家自然科学基金资助项目(60874012)

李明军(1981-),男,湖南永兴人,博士生,lim ingjun_8888@163.com.