航空拖曳诱饵空气动力及动态特性

芦艳龙 童中翔 王超哲 蒋 赟

(空军工程大学 工程学院,西安 710038)

航空拖曳诱饵空气动力及动态特性

芦艳龙 童中翔 王超哲 蒋 赟

(空军工程大学 工程学院,西安 710038)

航空拖曳式诱饵与被保护载机的相对空间位置及投放使用方法是诱饵能否成功干扰导弹的关键因素.针对传统有限段法的不足,提出改进的拖缆有限段法,将拖曳式诱饵的动态运动特性问题转变为拖曳线与拖曳飞机航迹轴系的夹角动态计算问题.通过分析拖曳飞机的速度矢量与拖曳线的几何关系,建立了拖曳式诱饵对拖曳载机的动态跟随模型.仿真计算了拖曳飞机机动飞行时,拖曳式诱饵的动态运动特性,结果证明算法简单有效,较好地模拟了其动态跟随特性.

拖曳式诱饵;动态特性;空气动力;计算机仿真

国外拖曳式诱饵 ALE-50/55等已经装备部队,在对抗导弹攻击时,发挥了重要的作用.目前,我国也处在研制和试验该型诱饵阶段.诱饵能否干扰成功,首先取决于诱饵是否位于导弹导引头视场角内,因此,诱饵和载机的相对空间位置就显得至关重要.计算二者的相对位置主要有以下几种模型[1]:“直线线性弹簧模型”,只近似考虑了弹性变形因素,但没有考虑拖曳线的重量和动力特性;“刚化柔性悬索模型”,只考虑了拖曳线的重量和弯曲变形因素,模型简单,便于计算,但没有考虑拖缆的伸长变形以及空气动力的影响;“等距约束模型”,既没有考虑拖曳线的重量及空气动力因素,也没有考虑拖曳线的伸长和弯曲变形因素;“刚化柔性体模型”,分析了拖曳线的自身重量及空气动力和弯曲变形的因素,但模型较繁琐,计算复杂,且没有考虑拖曳线伸长变形的情况;“完全柔性体模型”,虽然最完备,但模型中出现了多种耦合因子,使得模型的建立与求解变得非常困难.文献[2]模型以有限元法为基础,采用有限差分法进行数值求解;文献[3]将多体系统动力学理论直接应用于缆索,提出了有限段法,该算法应用了多刚体理论,但没有考虑拖曳线的特点,文献[2-3]提到的两种方法模型复杂,计算量较大,都不满足诱饵研制阶段快速仿真要求.

另外,国内文献着重研究水下拖缆系统的运动特性[4]以及航空拖曳诱饵的电磁干扰特性,都取得了许多成果,但在航空拖曳诱饵动态特性这一领域的研究较少,所以本文在参考以上文献的基础上,提出一种航空拖曳式诱饵动态运动快速准确的计算模型,来计算航空空间和临近空间诱饵和载机的相对空间位置,最后通过仿真算例分析,证明模型的正确性和适用性.

1 总体建模思路

拖曳系统是由拖曳式诱饵、拖曳线,拖曳飞机3者组成的多体约束系统,结构如图 1所示.

图 1 拖曳系统示意图

当拖曳飞机飞行时,拖曳线在诱饵气动拉力的作用下,近似为直线,故只考虑其伸长变形即可.这是因为航空拖曳式诱饵一般质量较小,拖曳线使用光纤等质量较轻的材料.欲求拖曳式诱饵与拖曳载机的相对位置,只需求出拖曳线与拖曳飞机航迹轴系的两个偏转角度仰角 αT和偏角βT,这两个角度的定义详见文献[5],通过这两个角度即可算出拖曳式诱饵在拖曳飞机航迹坐标系中的坐标,进而得出该诱饵在地轴系中的坐标.为了研究方便,将拖曳飞机运动特性分为两种,稳定直线飞行和机动飞行,其中稳定直线飞行部分(静态特性)详见文献[5],下面主要研究拖曳飞机机动飞行部分(动态特性).

1.1 拖曳飞机水平面机动飞行

拖曳飞机水平面速度矢量与拖曳线几何关系分析如图 2[5]所示.

飞机机动前,xh轴和 AB在同一个铅垂面内,故 βT=0.如图 2所示,将 V′h和 α′h分别向 Oxh,Ozh轴上进行分解投影.v′hx+a′hx与机动前速度方向 xh轴重合 αT的计算见文献[5].

则 zh轴上的等效平均速度大小[6]为

图 2 拖曳飞机水平面速度矢量与拖曳线几何关系

式中,L为拖曳线长度.

1.2 拖曳飞机铅垂面机动飞行

拖曳飞机铅垂面速度矢量与拖曳线几何关系分析如图 3所示.

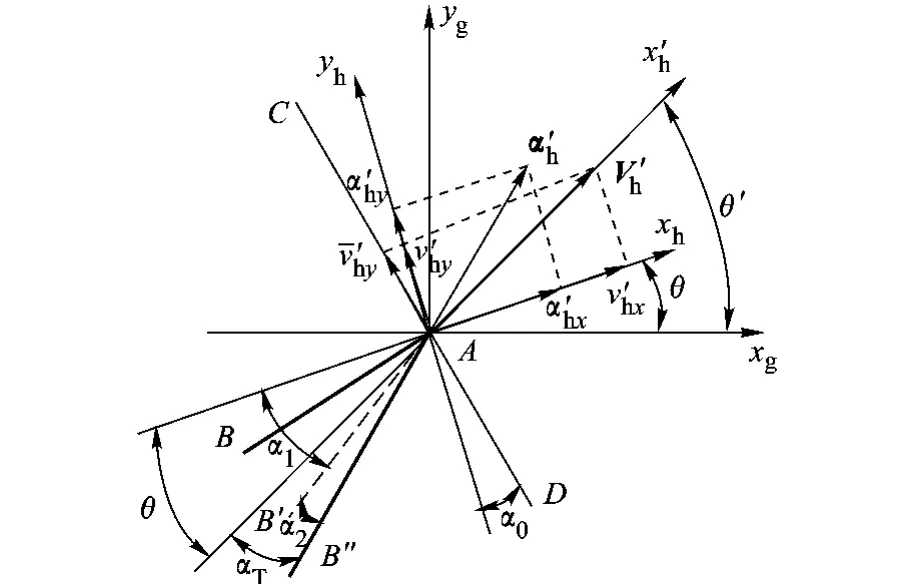
图 3 拖曳飞机铅垂面速度矢量与拖曳线几何关系

如图 3所示 ,βT=0,v′hx+a′hx与机动前速度方向 xh轴重合,仰角 α0,α1的计算见文献[5].

从图2中可以看出，当沙门氏菌纯培养物浓度为5.6×107CFU/g～5.6×104CFU/g时，荧光曲线出现明显的扩增峰，仪器自动判定为阳性；当培养物浓度为5.6×103CFU/g时，荧光曲线平缓，未出现扩增峰，判定为阴性。因此，研究所建立RF-LAMP检测人工污染肉制品的检出限为5.6×104CFU/g。

yh轴上的平均速度大小 v-hy计算公式同式(1).由于 v-hy的方向不垂直于拖曳线 AB,则

式中,ωα为拖曳线绕 Ozh轴转动角速度.

1.3 拖曳式诱饵动态特性

当拖曳飞机铅垂面水平机动飞行时,对铰接A点的俯仰力矩分析如图 4所示.

图 4 铰接A点俯仰力矩分析

当拖曳飞机速度矢量改变时,诱饵力矩不再平衡,则有

式中,I=1/3mD×L2+mT×L2为拖曳线和诱饵系统的转动惯量,mD为拖曳式诱饵质量,mT为拖曳线质量;εαT为拖曳线绕 Ozh轴转动角加速度[6].

式中,Cq为诱饵垂直于 AB的侧向气动阻力系数;vαT为诱饵垂直于 AB的速度大小[7];S为诱饵浸润面积.

偏转力矩分析同理.

1.4 拖曳式诱饵地面坐标计算

设铰接 A点在飞机航迹坐标系中坐标 rA,铰接 A点相对飞机重心的位置如图 5所示.

图5 铰接A点在飞机体轴系中位置

诱饵在拖曳飞机航迹坐标系中的坐标 r为

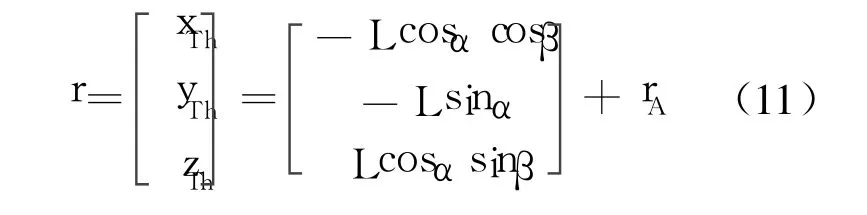
拖曳式诱饵在地轴系中的坐标 rg为

式中,rP为拖曳飞机重心地轴系坐标为飞机航迹轴系到地面轴系的坐标转换矩阵.

2 仿真实验分析

取拖曳线密度 ρT=0.2kg/m;拖曳线初始长度 L0=80m;mT=50 kg;诱饵的纵向阻力系数Cx=0.3;Cq=16.65;S=0.2m2;拖曳线弹性刚度KS=2000N/m.

算例 1 设拖曳飞机在高度1,3,5km稳定直线飞行,在诱饵实际开发中,由于拖曳线的可靠性问题很重要,所以必须计算拖曳线的拉力特性,算法见文献[5].

图 6中上半部分 θ=30°,a=5m/s2,在 1 km高度时,拉力从 1856N非线性增加到6458N,高度每增加 1km,拉力增大约 1150N.结果表明随着高度的增加,拉力非线性地减小.下部分 θ=0,α=0.相比上半部分,拉力减小幅度约为 31%.

图 6 拖曳线拉力与拖曳飞机速度关系

算例 2 当拖曳飞机水平定常盘旋飞行时,可以通过侧向平均速度的计算,间接描述诱饵的动态跟随特性,取飞机高度 5km,速度 250m/s,航向角速度分别为 1,3,6(°)/s时,计算诱饵侧向动态特性.

图 7表明随着航向角速度的增加,速度分量在拖曳线上偏转分量非线性增加,故拖曳线进入稳定状态的侧向平均速度和时间都呈非线性增大.侧向平均速度稳定值分别为 1.5,4.1,8.4;所需的稳定时间分别为 0.8,1.2,1.5 s.

算例 3 取拖曳飞机平飞加速区间为 200～250m/s,仿真计算仰角的动态特性.

图 8分别在加速度为 3m/s2,1m/s2时进行计算,由于加速度增大,气动力和惯性力增大,使俯仰力矩增大,仰角能够较快地逼近稳定值,其震荡幅度随着时间逐渐衰减.

图 7 侧向平均速度与时间关系

图 8 拖曳仰角随时间变化关系

图 9 拖曳俯仰角速度随时间变化关系

图 10 拖曳俯仰角加速度随时间变化关系

由图9、图10可见,拖曳仰角角速度、角加速度的震荡幅度随着时间逐渐衰减,气动阻尼系数越大,衰减越快.

3 结 论

通过分析拖曳飞机的速度矢量与拖曳线的几何关系,建立了拖曳式诱饵对拖曳载机的动态跟随模型,并进行了仿真实验,结果表明:①航迹俯仰角和加速度相对高度对仰角和拖曳线拉力的影响较大.②在高度 5km,速度 250m/s时,随着航向角速度的增加,拖曳线进入稳定状态的偏角和时间都非线性增大.航向角速度每增加 1(°)/s,偏角稳定值增加约 0.31°.③由诱饵动态摆动特性仿真得出,约 100 s后,诱饵趋于稳定,除此之外,大气扰动的影响不能忽略,这部分研究将在以后进行.

References)

[1]Ken Norlin and Jim Murray.Simulations in support of towed flight demonstration[J].National Aeronautics and Space Administration,1998,35(103):85-89

[2]Allow C M,Schechter S.Numerical simulation of undersea cable dynam ics[J].Ocean Engrg,1983,10(6):443-457

[3]Kammen JW,Huston R L.Modeling of submerged cable dynamics[J].Computers and Structures,1985,20(103):623-629

[4]王飞,黄国木梁,邓德衡.水下拖曳系统的稳态运动分析与设计[J].上海交通大学学报,2008,42(4):679-684 Wang Fei,Huang Guoliang,Deng Deheng.The design and steady state simulation of underwater towed system[J].Journal of Shanghai Jiaotong University,2008,42(4):679-684(in Chinese)

[5]芦艳龙,童中翔,于锦禄,等.拖曳式诱饵运动特性建模与仿真计算[J].飞行力学,2010,28(5):24-26 Lu Yanlong,Tong Zhongxiang,Yu Jinlu,et al.Modeling and simulation calculation for movement characteristic of towed decoy[J].Flight Dynamics,2010,28(5):24-26(in Chinese)

[6]哈尔滨工业大学理论力学教研室.理论力学[M].北京:高等教育出版社,2002:189-193 Harbin institute of technology academic mechanics staff room.Academic mechanics[M].Beijing:Higher Education Press,2002:189-193(in Chinese)

[7]方振平,陈万春,张曙光.航空飞行器飞行动力学[M].北京:北京航空航天大学出版社,2005:105-108 Fan Zhenping,Chen Wanchun,Zhang Shuguang.Aviation aerocraft flight dynamics[M].Beijing:Beijing Aeronautics and Astronautics Press,2005:105-108(in Chinese)

(编 辑 :李 晶)

Aerodynamic and dynamic characteristics of aeronautic towed decoy

Lu Yanlong Tong Zhongxiang Wang Chaozhe Jiang Yun

(Engineering Institute,Air Force Engineering University,Xi'an 710038,China)

The relative space position between aviation towed decoy and plane which is protected and release method of aviation towed decoy are the main factors that influence the result when missile is jammed by decoy.A new finite segment method was developed to make up the deficiencies of conventional finite segment method.Aerodynamic movement characteristics of aeronautic towed decoy were transformed to the question how tomodel and compute angles between tow and towing aircraft track coordinates.The geometry relationship between velocity vector of towing aircraft and tow was analyzed,so dynamic fallow models of tow and towing aircraft were established.The dynamic characteristics of towed decoy were calculated when towed aircraft does different flights.The result indicates that the arithmetic is simple,valid and better to simulate decoy's dynamic characteristics.

towed decoy;dynamic characteristics;aerodynamics;computer simulation

TP 391.9

A

1001-5965(2011)04-0395-04

2010-01-18

国家自然科学基金资助项目(60772162)

芦艳龙(1982-),男,山西汾阳人,博士生,lyl_key@163.com.