我国石油价格联动波动率研究

○石 艺 刘 敏

（武汉大学经济与管理学院 湖北 武汉 430072）

一、引言

近几年来，国际石油价格可谓一波三折。2007年初原油价格大约50美元/桶，而一年之内国际油价上涨了大约58%，是近10年来涨幅最大的一年。2008年6月25日公布的数据显示，欧佩克市场监督原油一揽子平均价24日突破每桶131美元关口，达到每桶131.25美元，再次创下历史新高。2009年受欧元对美元剧烈下滑和希腊危机的影响，在国际期货市场投机行为的助推下，国际原油价格波动剧烈。国际原油价格的超常波动将对国际能源市场、国际经济局势、相关产业产生了巨大的冲击和影响。

石油作为“工业血液”的战略地位，其价格影响因素之复杂远非一般商品所能相提并论。在国际石油市场上，油价除了围绕国际石油价值这个轴心随供求关系的变化而不断上下波动外，还由于石油本身具有的特殊性受到其他诸多不确定性因素的影响，如政治、军事因素、石油消费国对策、石油期货市场投机等因素。因此，对国际油价波动特点以及影响因素进行实证研究，厘清油价运行规律及其长短期影响因素，对于预测油价变化，制定相关经济政策，具有重要的意义。

波动率在金融衍生产品定价、投资组合风险管理、对冲投资策略中具有重要作用，在现代金融理论中，广泛地以波动率来代表风险，并可用收益的方差进行测度。传统的计量经济学模型往往假定样本的方差恒定不变，但随着金融理论的深入发展，这一假设已逐渐呈现出其不合理的方面。大量的有关金融数据的实证研究表明用来表示不确定性和风险的方差是随时间而变化的。ARCH类模型已经被国外研究者广泛地运用到股票的波动性研究之中。

本文基于波动率预测的方法分析比较了国际国内具有代表性的石油价格的波动率。之后详细讨论了ARCH模型及其扩展形式，并对随机波动率模型做了详细介绍，提出了符合我国油价波动率变化的预测模型。

二、理论简介

近十年来，波动率是在金融领域中非常活跃和成功的研究课题之一。波动率是资产收益不确定性的衡量，很多学者对其进行了深入研究，这些研究广泛应用于股票市场、债券市场和外汇市场。目前学者们已经提出很多方法来拟合金融时间序列的波动率特征，代表性的介绍如下。

1、历史波动率与隐含波动率法

历史波动率是根据过去数据计算的波动率，常用的计算方法有算术平均法、滑动平均法、指数平滑法（Exponentially WeightedMovingAverage，简称EWMA）。在上世纪七十年代以前，经典的金融经济分析都假定波动率是恒定的，未详细考虑波动率随时变化的情形。期权隐含波动模型首先由Latane和Rendleman在1976年提出。其基本原理是依据Black-Scholes期权定价公式从期权价格倒推出市场的波动率，这个波动率常被称为隐含波动率。由于期权价格反映的是市场未来的波动率，因此应用该模型可以预测波动率。但由于原假设建立在波动率恒定的基础之上，隐含波动率往往是一个有偏估计量。Canina、Figlewski（1993）通过研究S＆P500指数的波动率，发现隐含波动率的估计效果还不如历史波动率。Fleming（1997）更进一步表明S＆P500指数的隐含波动率是上偏估计量。另一些学者提出运用近似数值算法来改进隐含波动率的估计效果。然而由于计算过于复杂，在估计效果方面并没有多少改进。

2、GARCH 模型

传统的经济计量模型假定样本的方差保持不变。但随着经济理论的发展及实证工作的深入，学者们发现这一假设不甚合理。越来越多的研究结果表明，经济类时间序列数据，诸如股票价格、通货膨胀率、利率、外汇汇率等，经常出现方差随时间变化的特点。Mandelbrot（1963）观察经济随机变量分布的厚尾性。Engle（1982） 的 ARCH （AutoregressiveConditional Heteroskedasticity）模型捕捉到了经济类时间序列数据的方差的波动聚集性。至今，它们已被极广泛地应用于金融领域的非线性时间序列模型，以应付高度波动并且难以预测的金融数据。在ARCH模型的实际应用中，往往需要构造一个有很大的移动平均阶数，因此，为了克服这种方法的生硬性以及随意性，Bollerslev（1986）提出了一种更灵活的GARCH模型，它是最重要的一种ARCH模型扩展形式，模型等价于一个无限阶、参数呈指数递减的ARCH模型，因此GARCH可以用较少的参数来反映方差的持续性。Akgiray（1989）证实GARCH对股票指数日数据的模拟效果优于原始的ARCH模型，Campbell、Hentschel（1992），Engle、Ng（1991），Pagan、Schwert（1990）等的实证应用则证实 GARCH（1，1）或 GARCH（1，2）能够提供较理想的数据模拟与预测效果。

三、实证分析

1、数据来源

北美西得克萨斯（WTI）原油现货价格（FOB）代表国际油价水平，油价单位为美元/桶，数据采用日度形式，区间为2008年6月至2009年6月，共56个数据。数据来源于浙江塑料城网上交易市场。

大庆和胜利油田就油气探明储量和年产量而言，是我国主要的产油区。它们的原油价格基本上代表了我国整体原油价格水平。本文采用了大庆的每日收盘价作为研究对象，区间同上。数据来源于中国石油期货网。

2、研究设计与实证结果

（1）GARCH（1，1）模型对 Wti的波动率序列进行参数估计

其一，GARCH（1，1）模型估计结果，如表 1。

表 1 GARCH（1，1）模型参数估计结果

其中，γ=ω/（1-α-β）；σl为长期标准差，σl=；*表示p＆lt;0.10，**表示p＆lt;0.05，***表示p＆lt;0.01。

波动率方程为：

方差方程中的 ARCH 项（ε2t-1）和 GARCH 项（σ2t-1）的系数都是统计显著的，且两者系数之和为0.956209＆lt;1，满足GARCH（1，1）模型中参数的约束条件。由于系数之和非常接近于1，表明条件方差所受的冲击是持久的，即冲击对未来所有预测都有重要作用。

其二，事后检验——GARCH（1，1）模型的ARCH-LM检验。

下面是对GARCH（1，l）模型的方差方程的残差序列在滞后阶数等3时，异方差的ARCHLM检验的统计结果，如表2。

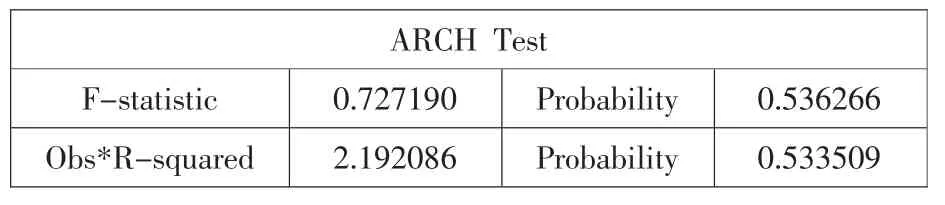
表2ARCHLM检验结果

此时的相伴概率为0.53，接受原假设，认为残差序列不存在ARCH效应，说明利用GARCH（1，l）模型消除了残差序列的条件异方差性。

结果分析：由上面对于国际原油价格Wti的波动率分析可知，用GARCH（1，1）模型来描述，其余的估计结果和算术平均历史波动率分析的结果基本相符，波动率均为0.02左右。

（2）ARCH类模型对大庆油价的波动率序列进行参数估计

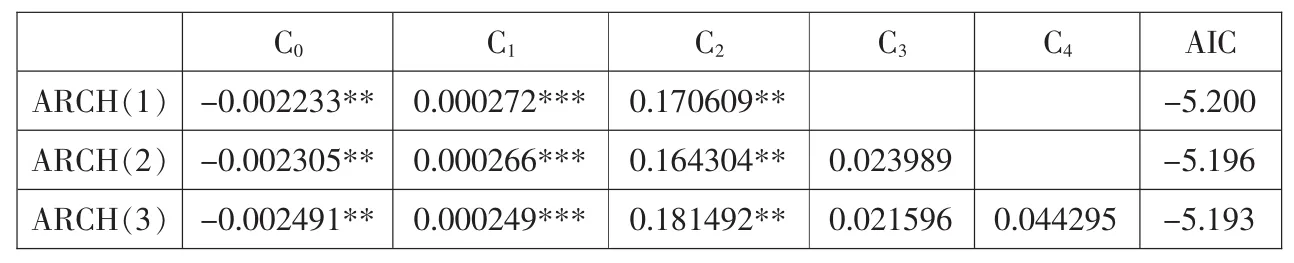
表3ARCH类模型拟合结果

其一，用 ARCH（1），ARCH（2），ARCH（3）拟合的估计结果，分别选取 ARCH（1），ARCH（2），ARCH（3）进行估计，结果如表3。

由表3，大庆油价波动率的模型估计中，各项参数均显著的是ARCH（1），Q-检验在5%的水平上显著，所以拟合最好的模型是 ARCH（1）。

其二，事后检验——ARCH（1）模型的ARCH-LM检验。下面是对ARCH（1）模型的方差方程的残差序列在滞后阶数等于3时，异方差的ARCHLM检验的统计结果，如表4。

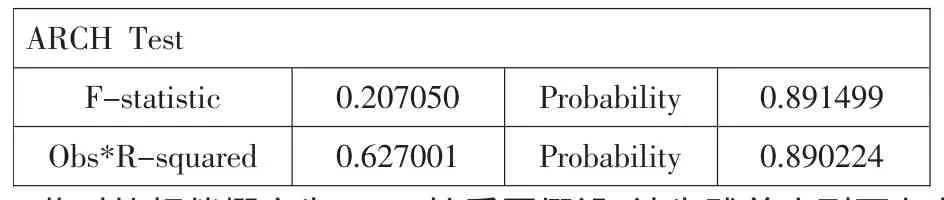
表4ARCHLM检验结果

此时的相伴概率为0.89，接受原假设，认为残差序列不存在ARCH效应，说明利用ARCH（1）模型消除了残差序列的条件异方差性。

结果分析：在 ARCH（1）、ARCH（2）、ARCH（3）模型的定量分析下，发现大庆石油价格波动率拟合最好的是ARCH（1）模型。

四、结论与建议

本文通过研究具有代表性的国际原油价格Wti和国内大庆石油价格的波动率，利用算术平均法计算出平均历史波动率。通过比较分析发现，国内油价波动率的波动幅度与国际油价波动较为一致，且较低于国际水平，这主要是受到我国石油需求现状决定的。根据石油价格波动的特点，本文还用ARCH族模型对波动率进行研究，结果发现用GARCH（1，1）模型模拟的Wti波动率的估计结果和算术平均历史波动率分析的结果基本相符。同时，通过分析比较 ARCH（1），ARCH（2），ARCH（3）的检验结果，发现ARCH（1）是国内石油价格（大庆石油价格）最好的估计模型。

[1]Kim S， Nshephard， Schib.Stochastic Volatility: Likelihood Inference and Comparison with ARCH Models [J].Review of Economic Studies，1998（65）.

[2]Latane， H.and R.J.Rendleman.Standard Deviations of Stock Price Ratios Implied by Option Premia [J].Journal of Finance，1976（31）.

[3]Mandelbrot， B.The variation of certain speculative prices[J].Journal of Business，1963（26）.

[4]Zakoian J M.Threshold Heteroskedastic Models [Z].Manuscript，CREST，INSEE，Paris，1990.

[5]陈守东、陈雷、刘艳武：中国沪深股市收益率及波动性相关分析[J].金融研究，2003（7）.

[6]李亚静、何跃、朱宏泉：中国股市收益率与波动性长记忆性的实证研究[J].系统工程理论与实践，2003（23）.

[7]唐齐鸣、陈健：中国股市的ARCH效应分析[J].世界经济，2001（3）.