整体叶轮展成电解精加工成型规律及运动设计

吴 锐，徐家文

(南京航空航天大学江苏省精密与微细制造技术重点实验室，210016南京，wurui-ly@126.com)

数控展成电解加工技术是一种将数控技术和电解技术相结合的新型制造技术，它既有数控加工的柔性，又具有一般电解加工的优点.数控展成电解加工技术在整体叶轮加工中具有独特的优势［1-4］，它通过利用简单形状的阴极做展成运动，有效地解决难切削材料零件复杂型面的加工难题［5-8］.但电解加工是非接触式加工，在加工过程中工具阴极与工件之间始终有一加工间隙，这就决定了展成电解加工中工具阴极运动轨迹的设计不同于数控铣等切削加工中刀具轨迹的设计［9-10］.阴极运动设计包括阴极运动轨迹设计和运动参数的确定，为了获得高精度的整体叶轮叶片型面，在进行阴极运动设计时必须要考虑工具阴极的成型规律特点.不同形状的阴极会有不同的成型规律模型，但是不同阴极成型规律研究的基本思路是相通的.

本文以展成电解精加工直纹面叶轮为例，通过对精加工阴极表面进行离散化处理的方法，研究其成型规律.建立了电解加工间隙的数学模型，并利用这一模型对某型直纹面整体叶轮叶片型面的精加工阴极的展成运动进行了设计.以阴极成型规律为基础的展成运动设计方法，可以快速、高效地进行整体叶轮叶片型面展成电解加工阴极运动设计.

1 整体叶轮精加工阴极成型规律

在展成电解精加工整体叶轮叶片型面时，采用内喷式阴极，叶片型面的加工过程如图1所示.

图1 叶片型面展成加工示意图

阴极的运动轨迹由很多小的直线段近似拟和，其中每一直线段即每一数控段的加工可以近似认为是平面加工.为了便于分析电解加工的成型规律，将一数控段的加工过程简化如图2所示的平面加工.

图2 成型规律模型示意图

把阴极工作面看作是由若干平行于加工面的微小工作面组成，则加工间隙是由这些微小工作面共同作用形成.阴极的进给速度与工件平面平行，即在工件平面法线方向没有进给，则阴极工作面上的各个微小工作面对应的加工间隙就可以用侧面间隙成型规律来分析，只是因为各个微小工作面依次连续加工造成各个微小加工面的初始加工间隙不同，后一个微小加工平面的初始加工间隙取决于前一个微小加工平面形成的加工间隙，整个阴极工作面形成的加工间隙就是最后一个微小加工平面形成的加工间隙.

电解加工中侧面间隙成型规律与阴极在进给方向上的长度有关，当阴极工作面与工件平面有一夹角β时，阴极工作面在进给方向有效工作长度为(2L+Lo)cos β，其中L为阴极出液口两边阴极工作面的长度，Lo为阴极出液口长度.相应的每一微小工作面在进给方向的有效工作长度为lcos β，其中l为每一微小工作面的长度.

当夹角β＞0°时，用下列公式计算加工间隙Δb和去除材料厚度h:

当夹角β＜0°时，用下列公式计算加工间隙Δb和去除材料厚度h:

式中，KU为电解加工常数，与工件材料、电源、电解液的选择有关，当电解加工工艺参数确定后为一定值.

为了验证上述公式的正确性，用图1所示阴极进行了不同β、vf值情况下的电解加工平面实验，以便了解去除材料厚度h与β、vf之间的关系.实验中，阴极工作面上L=1 mm，Lo=0.5 mm，取离散面l=0.1 mm，电解液为质量分数20% NaNO3溶液，加工温度为28～32℃，加工电源为脉冲电源:峰值电压15 V、频率25 kHz、占空比0.6，电解液进口压力为0.7 Pa，当Δ0=0.1 mm时，h与vf、β的实验数据如表1、2所示，计算值与实测值的平均误差＜0.02 mm，本文所建立的成型规律模型可以用于预测实际加工间隙.

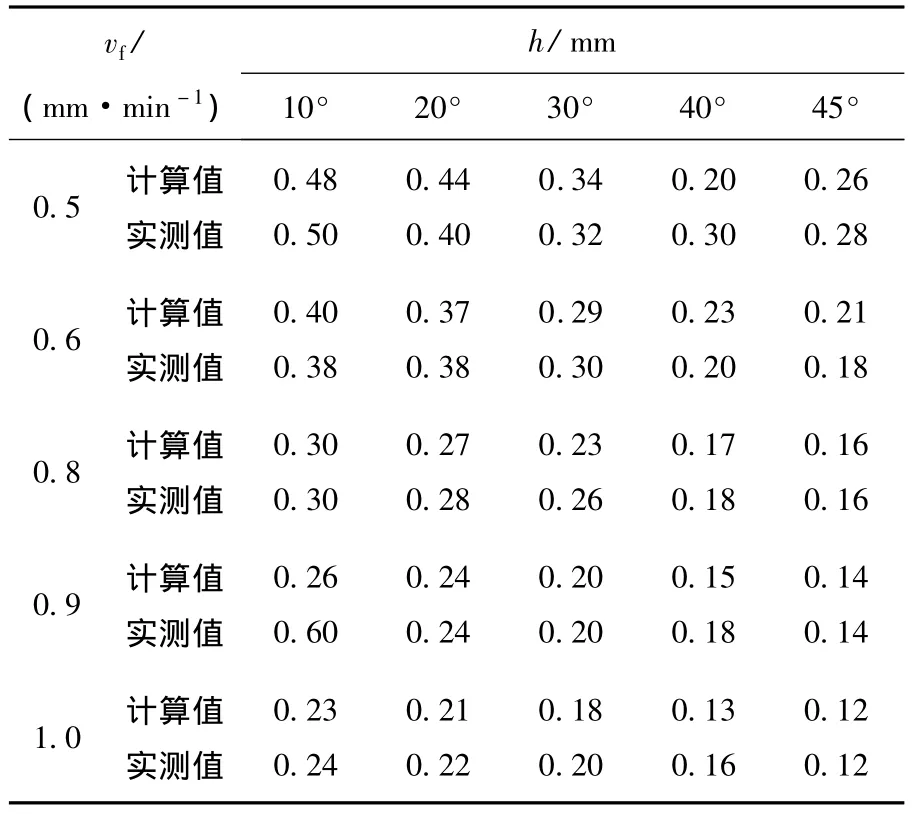
表1 β＞0，Δ0=0.1 mm时，h与vf、β的关系

表2 β＜0，Δ0=0.1 mm时，h与vf、β的关系

2 叶片型面精加工运动设计

2.1 阴极工作刃边运动轨迹设计

整体叶轮的叶片型面一般以列表形式给出某一叶片型面上若干截面Y=Yi(i=1，2，…，m)内的若干数据点，以及进气边圆弧和排气边圆弧的圆心位置和半径，没有确定的数学表达式，因此，要先对型值点数据进行处理，以便分析和确定阴极工作刃边相对于叶轮的运动轨迹.

叶片型面是由阴极的直线刃边通过一定的轨迹运动得到的，工具阴极运动轨迹面与叶片型面之间始终有一初始加工间隙Δ0，因此，阴极刃边的运动轨迹不是叶片型面拟合直纹面的母线，而是拟合直纹面上各母线做法向等距偏置后得到的直线，但由于各个Yi截面内拟合曲线的弯曲角度变化情况不同，拟合出的直纹面上各母线做法向等距偏置后有可能不与Zi截面平行，且各母线偏置后与Zi截面的夹角也不尽相同，若以直纹面母线偏置后得到的直线作为运动轨迹，则阴极直线刃在数控加工运动中相对Zi截面就有一个摆动，增加了数控运动的复杂性，也会降低加工型面的光滑连续性.因此，得到叶片型面在Yi截面内的拟合曲线MPi、MBi(下标P、B分别对应叶盆面和叶背面)后，先在各Yi截面根据拟合曲线方程把给定型值点在拟合曲线法向偏置一个距离Δ0，再对偏置后得到的点进行三次B样条曲线拟合，得到一组叶片轮廓曲线的偏置曲线CPi、CBi，其方程可写为

其中nPi(u)、nPi(u)分别为曲线MPi、MBi的单位法矢.

用一组等距平面Z=Zi(i=0，1，…，n)与CPi、CBi相交，在各个Zi平面内对所得交点用最小二乘法进行直线拟合，并分别求出所得直线与叶根圆的交点PPi、PBi和与叶顶圆的交点QPi、QBi，得到的两组直线段LPi、LBi(i=0，1，…，n):

这两组直线段即为所求阴极工作刃精加工叶盆面和叶背面的运动轨迹，其设计方法如图3.

图3 阴极工作刃运动轨迹设计示意图

2.2 展成加工运动速度分析

整体叶轮的精加工过程中，工件和阴极之间的相对运动是X、Y、Z方向的平动及绕Z轴旋转的合成运动，工具阴极仅在Z向做直线运动，工件随工作台作X、Y方向直线运动和绕Z轴转动，此时各数控段的加工可以简化为如图4所示斜面加工.

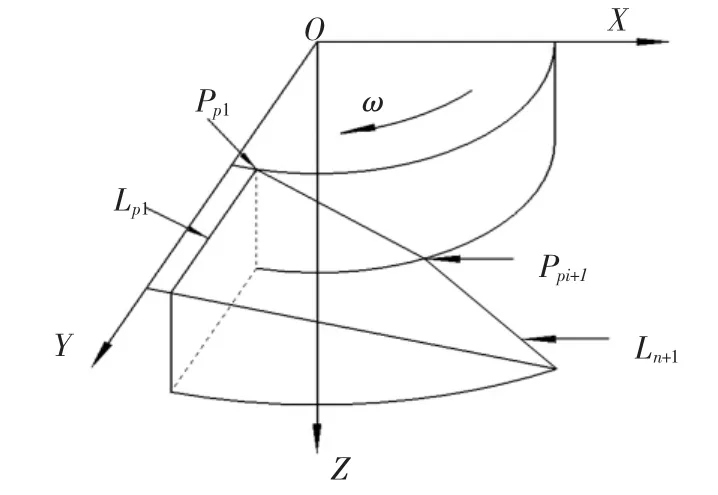
图4 每一数控段加工示意图

阴极相对于叶轮的合成进给速度为

阴极在Y方向移动量很小(仅为其他几个轴运动量的5% ～10%)，因此忽略Y方向的进给速度.此外，由于存在一个绕Z轴的转动，所以沿叶轮径向阴极进给速度会有差别，为简化数控运动参数的设计过程，把阴极工作刃在叶长中部的进给速度看作为整个阴极加工刃的进给速度，则阴极加工刃相对于叶片型面的合成进给速度可写为

阴极工作面与叶片型面夹角为叶片扭角β，在叶片加工过程中各数控段的β值不同，但在每一数控段中是以斜面代替曲面进行加工的，所以认为在每一段中β值是不变的.在进行阴极数控运动参数设计时，数控段的多少取决于Zi截面的划分，因此每一数控段在Z轴方向的移动量是已知的，其他各轴在每一数控段内的移动量要与Z轴方向的移动量相匹配，因此可以先确定每一数控段在Z轴方向的进给速度，根据前面分析得到: vfi=vzi/cos βi，各轴进给速度与Z轴进给速度的关系为

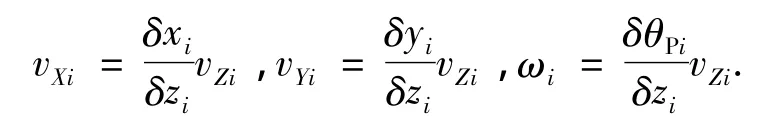
式中:δθPi为相邻直线段LPi+1与LPi的夹角，对叶盆面(对叶背面，下式中各变量下标P换为B即可)有

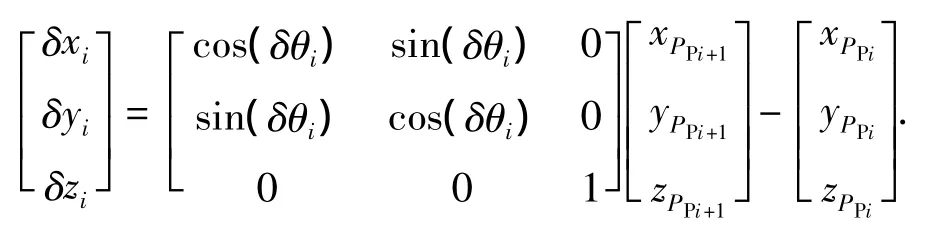
2.3 展成运动速度的确定

叶片精加工中，叶片扭角是已经给定的设计参量，不能随意改变，如本文所讨论的某直纹面叶轮叶盆面.β为 -20°～-45°，叶背面.β为-30°～60°，所以在展成电解加工过程中只有通过调整vf、.Δ0来控制去除材料的厚度h而得到理论的加工型面.

由前述成型规律数学模型，通过优化方法得到当Δ0=0.1 mm，h=0.3 mm时叶盆面和叶背面vf随β变动的关系曲线(如图5所示)，其中叶盆面β一直为负值，vf随β的增大而逐渐增大;而叶背面vf在β=0处有一明显的突变.实际加工中β＜0时阴极工作面的下刃边是主要加工刃，β＞0时主要加工刃则变为上刃边，即在β=0处完成主要加工刃边的变换.加工刃的变换是一个过程，为了避免在此处发生过切，需要阴极或以极快的速度完成主要加工刃的变换，或增大Δ0，使这一过渡过程的材料去除厚度降低到精度许可的范围.在试验加工中综合采用了这两种方法，使这一变换过程的阴极运动速度和Δ0相对于相邻数控段的变化不至于太大.

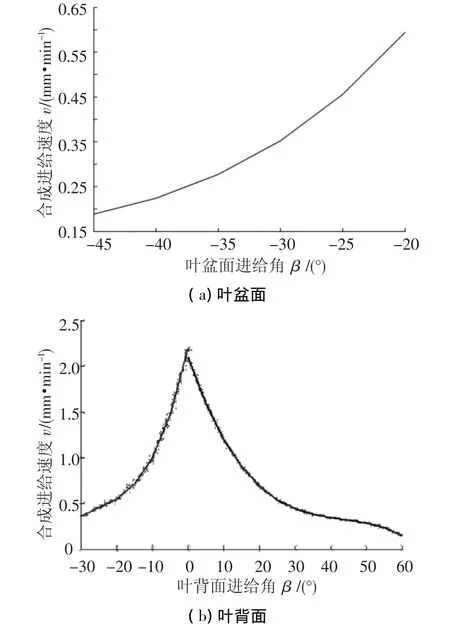
图5 合成进给速度vf与进给角β关系曲线

3 工艺实验

利用上述方法对某型整体叶轮展成电解精加工运动进行设计，并进行了加工实验.电解液为质量分数20%NaNO3溶液，加工温度为30℃，加工电压峰值15 V(脉冲电源:25 kHz，占空比0.6)，电解液进口压力为0.4 Pa.精加工后的叶片型面经三座标测量机检测，叶盆面余量小于0.20 mm，达到了叶片形面设计精度要求，叶背面最大余量不超出0.30 mm，极大地减小了后续的手工抛光工作量.

4 结论

1)对精加工阴极工作面进行离散化处理，研究其成型规律，建立了成型规律的数学模型.平面加工实验表明:该模型可以准确地反映阴极进给速度vf、阴极进给角度β和加工间隙Δb之间的关系.

2)利用成型规律模型对某型直纹面整体叶轮叶片型面的精加工阴极的展成运动进行了设计.叶片加工实验表明:以此为基础的展成运动设计方法可以快速有效地进行整体叶轮叶片型面展成电解加工阴极运动设计，精确地控制实际加工中去除材料的厚度，具有较高的工程实用价值.

［1］徐家文，云乃彰，严德荣.数控电解加工整体叶盘的研究、应用和发展［J］.航空制造技术，2003，(6):31-34.

［2］康敏，徐家文.精密展成电解加工整体叶轮的展成运动轨迹确定［J］.中国机械工程，2006，17(4):346-349.

［3］朱永伟，徐家文，赵建社.大扭曲叶片整体涡轮盘电解加工关键技术［J］.哈尔滨工业大学学报，2008，40 (5):783-787.

［4］XU Jiawen，YUN Naizhang，TANG Yangxin，et al.The modelling of NC-electrochemical contour evolution machining using a rotary tool-cathode［J］.Journal of Materials Processing Technology，2005，159:272-277.

［5］KOZAK J，FUDZYNSKI A F，DOMANOWSKI P.Computer simulation electrochemical shaping(ECM-CNC) using a universal tool electrode［J］.Journal of Materials Processing Technology，1998，76:161-164.

［6］KOZAKA J，CHUCHR M，RUSZAJ A，et al.The computer aided simulation of electrochemical process with universal spherical electrodes when machining sculptured surfaces［J］.Journal of Materials Processing Technology，2000，107:283-287.

［7］DOMANOWSKI P，KOZAK J.Direct and inverse problems of shaping by electrochemical generating machining［J］.Journal of Materials Processing Technology，2000，107:300-306.

［8］RUSZAJ A，ZYBURA-SKRABALAK M.The mathematical modelling of electrochemical machining with flat ended universal electrodes［J］.Journal of Materials Processing Technology，2001，109:333-338.

［9］GONG Hu，CAO Lixin，LIU Jian.Improved positioning of cylindrical cutter for flank milling ruled surfaces［J］. Computer-Aided Design，2005，37:1205-1213.

［10］于源，赖天琴，员敏，等.基于特征的直纹面5轴侧铣精加工刀位计算方法［J］.机械工程学报，2002，38 (6):130-133.